Question Number 103763 by mathmax by abdo last updated on 17/Jul/20
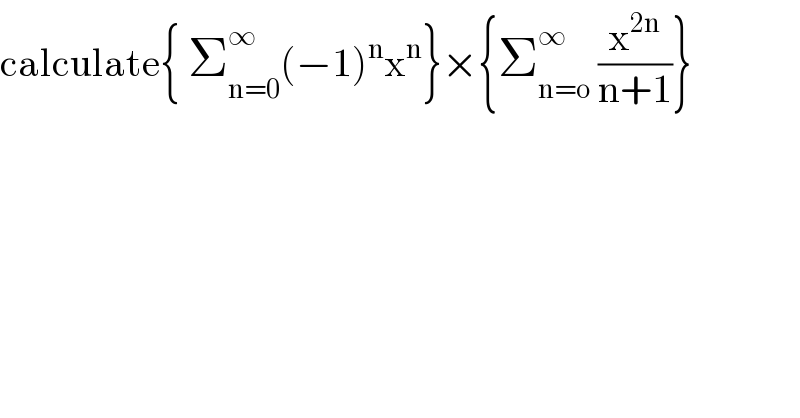
$$\mathrm{calculate}\left\{\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{x}^{\mathrm{n}} \right\}×\left\{\sum_{\mathrm{n}=\mathrm{o}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2n}} }{\mathrm{n}+\mathrm{1}}\right\} \\ $$
Answered by mathmax by abdo last updated on 18/Jul/20
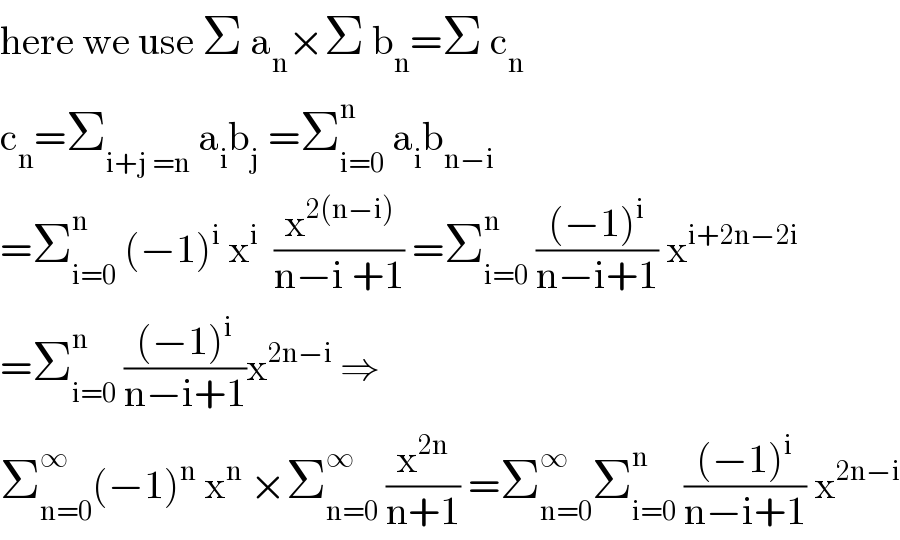
$$\mathrm{here}\:\mathrm{we}\:\mathrm{use}\:\Sigma\:\mathrm{a}_{\mathrm{n}} ×\Sigma\:\mathrm{b}_{\mathrm{n}} =\Sigma\:\mathrm{c}_{\mathrm{n}} \: \\ $$$$\mathrm{c}_{\mathrm{n}} =\sum_{\mathrm{i}+\mathrm{j}\:=\mathrm{n}} \:\mathrm{a}_{\mathrm{i}} \mathrm{b}_{\mathrm{j}} \:=\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{a}_{\mathrm{i}} \mathrm{b}_{\mathrm{n}−\mathrm{i}} \\ $$$$=\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\left(−\mathrm{1}\right)^{\mathrm{i}} \:\mathrm{x}^{\mathrm{i}} \:\:\frac{\mathrm{x}^{\mathrm{2}\left(\mathrm{n}−\mathrm{i}\right)} }{\mathrm{n}−\mathrm{i}\:+\mathrm{1}}\:=\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{n}−\mathrm{i}+\mathrm{1}}\:\mathrm{x}^{\mathrm{i}+\mathrm{2n}−\mathrm{2i}} \\ $$$$=\sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{n}−\mathrm{i}+\mathrm{1}}\mathrm{x}^{\mathrm{2n}−\mathrm{i}} \:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}} \:×\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2n}} }{\mathrm{n}+\mathrm{1}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \sum_{\mathrm{i}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{i}} }{\mathrm{n}−\mathrm{i}+\mathrm{1}}\:\mathrm{x}^{\mathrm{2n}−\mathrm{i}} \\ $$
