Question Number 85164 by mathmax by abdo last updated on 19/Mar/20
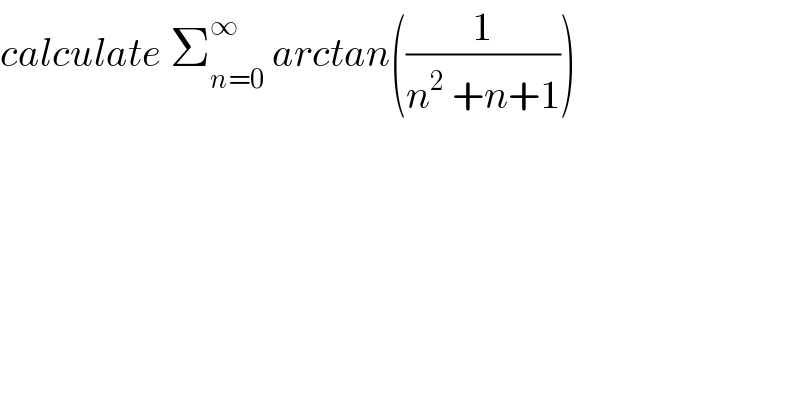
$${calculate}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{arctan}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+{n}+\mathrm{1}}\right) \\ $$
Commented by Cmr 237 last updated on 19/Mar/20

$${arctan}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}+\mathrm{1}}\right)={arctan}\left({n}+\mathrm{1}\right)−{arctan}\left({n}\right) \\ $$$${S}=−{arctan}\left(\mathrm{0}\right)=\mathrm{0} \\ $$
Commented by mind is power last updated on 19/Mar/20
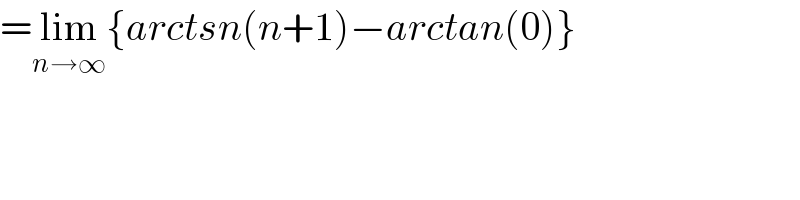
$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{{arctsn}\left({n}+\mathrm{1}\right)−{arctan}\left(\mathrm{0}\right)\right\} \\ $$
Commented by mathmax by abdo last updated on 19/Mar/20
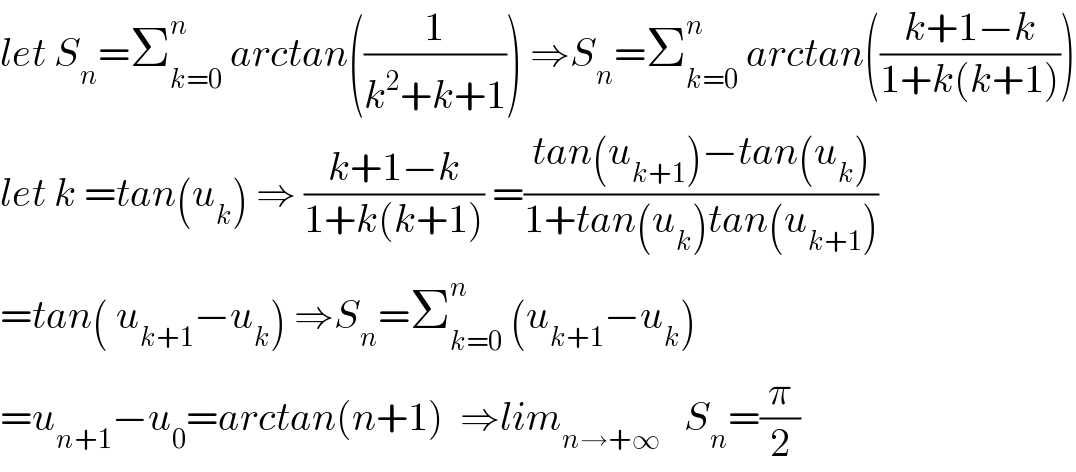
$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{arctan}\left(\frac{\mathrm{1}}{{k}^{\mathrm{2}} +{k}+\mathrm{1}}\right)\:\Rightarrow{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{arctan}\left(\frac{{k}+\mathrm{1}−{k}}{\mathrm{1}+{k}\left({k}+\mathrm{1}\right)}\right) \\ $$$${let}\:{k}\:={tan}\left({u}_{{k}} \right)\:\Rightarrow\:\frac{{k}+\mathrm{1}−{k}}{\mathrm{1}+{k}\left({k}+\mathrm{1}\right)}\:=\frac{{tan}\left({u}_{{k}+\mathrm{1}} \right)−{tan}\left({u}_{{k}} \right)}{\mathrm{1}+{tan}\left({u}_{{k}} \right){tan}\left({u}_{{k}+\mathrm{1}} \right)} \\ $$$$={tan}\left(\:{u}_{{k}+\mathrm{1}} −{u}_{{k}} \right)\:\Rightarrow{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\left({u}_{{k}+\mathrm{1}} −{u}_{{k}} \right) \\ $$$$={u}_{{n}+\mathrm{1}} −{u}_{\mathrm{0}} ={arctan}\left({n}+\mathrm{1}\right)\:\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:\:\:{S}_{{n}} =\frac{\pi}{\mathrm{2}} \\ $$
