Question Number 147862 by mathmax by abdo last updated on 24/Jul/21
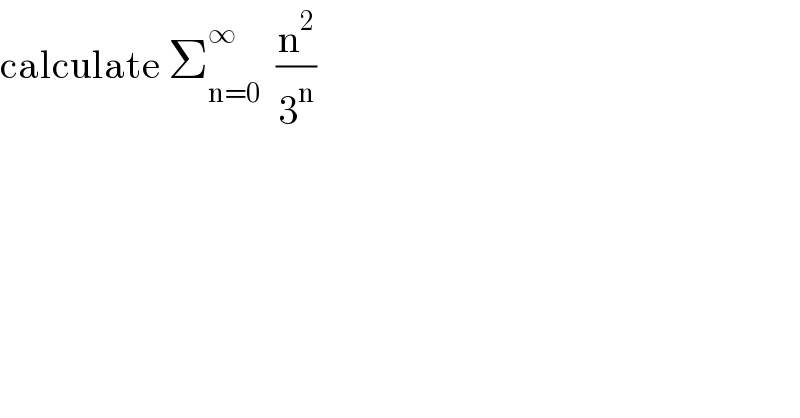
$$\mathrm{calculate}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{n}} } \\ $$
Answered by qaz last updated on 24/Jul/21
![Σ_(n=0) ^∞ (n^2 /3^n )=(xD)^2 ∣_(x=(1/3)) Σ_(n=0) ^∞ x^n =(x^2 D^2 +xD)∣_(x=(1/3)) (1/(1−x)) =[((2x^2 )/((1−x)^3 ))+(x/((1−x)^2 ))]_(x=(1/3)) =((x^2 +x)/((1−x)^3 ))∣_(x=(1/3)) =(3/2)](https://www.tinkutara.com/question/Q147864.png)
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{n}} }=\left(\mathrm{xD}\right)^{\mathrm{2}} \mid_{\mathrm{x}=\frac{\mathrm{1}}{\mathrm{3}}} \underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{x}^{\mathrm{n}} =\left(\mathrm{x}^{\mathrm{2}} \mathrm{D}^{\mathrm{2}} +\mathrm{xD}\right)\mid_{\mathrm{x}=\frac{\mathrm{1}}{\mathrm{3}}} \frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}} \\ $$$$=\left[\frac{\mathrm{2x}^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }+\frac{\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\right]_{\mathrm{x}=\frac{\mathrm{1}}{\mathrm{3}}} =\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }\mid_{\mathrm{x}=\frac{\mathrm{1}}{\mathrm{3}}} =\frac{\mathrm{3}}{\mathrm{2}} \\ $$
