Menu Close

calculate-n-0-n-n-1-4-2n-1-2-

Tinku Tara 0 Comments
Pin




Question Number 51185 by Abdo msup. last updated on 24/Dec/18
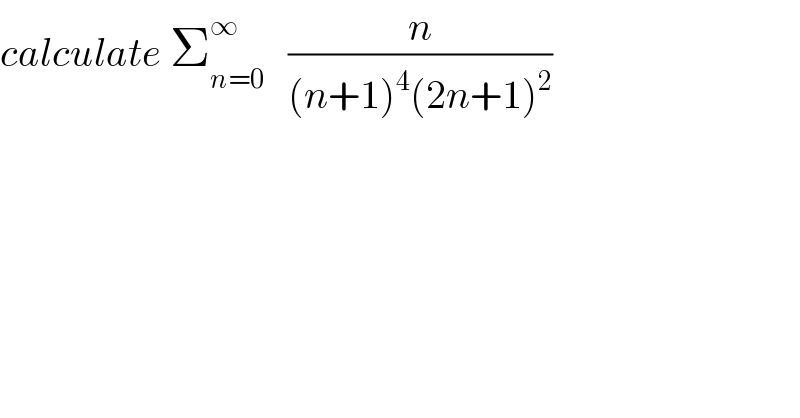
calculate Σ_(n=0) ^∞ (n/((n+1)^4 (2n+1)^2 ))
calculate∑n=0∞n(n+1)4(2n+1)2
Commented by Abdo msup. last updated on 30/Dec/18
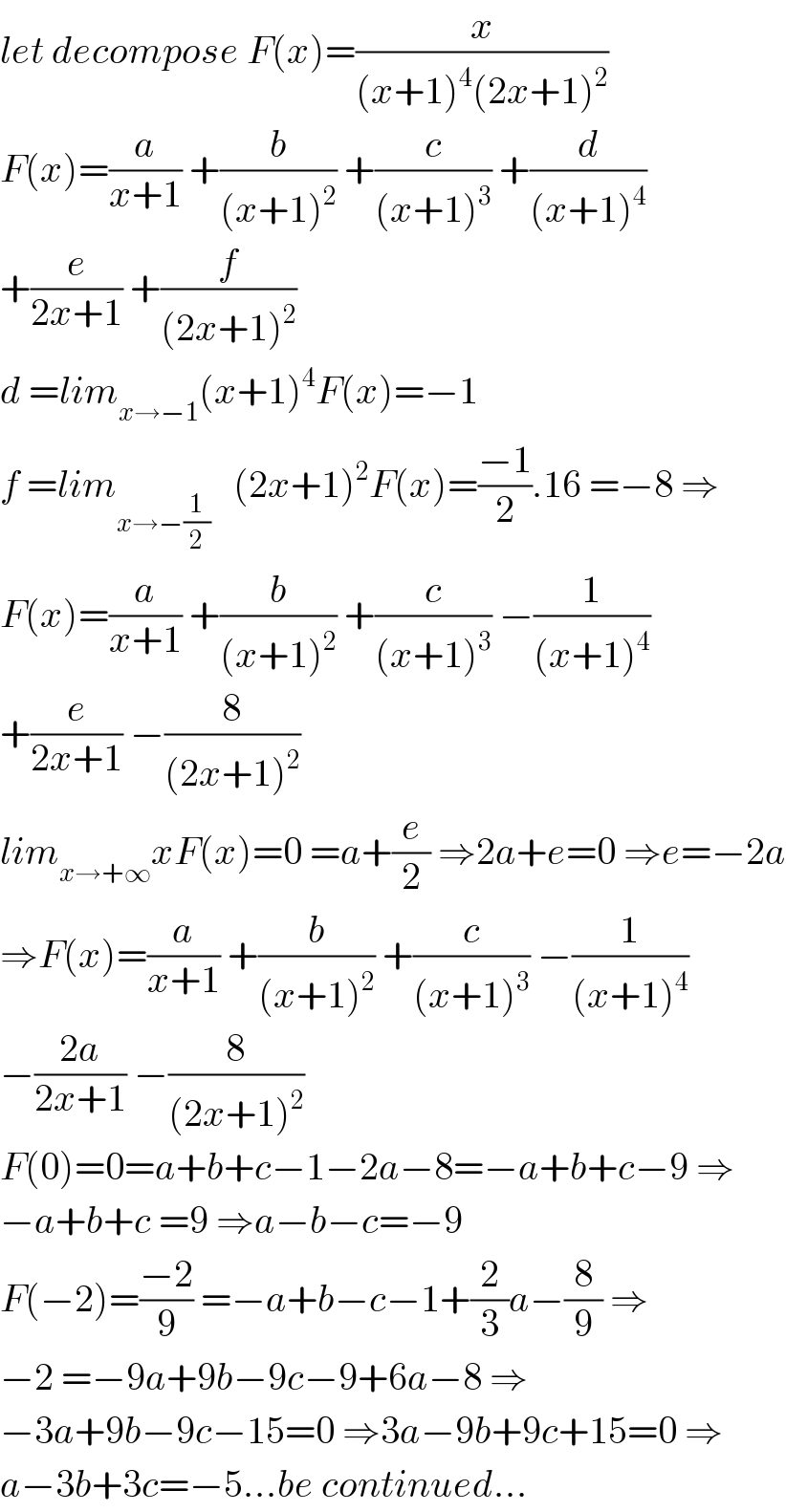
let decompose F(x)=(x/((x+1)^4 (2x+1)^2 )) F(x)=(a/(x+1)) +(b/((x+1)^2 )) +(c/((x+1)^3 )) +(d/((x+1)^4 )) +(e/(2x+1)) +(f/((2x+1)^2 )) d =lim_(x→−1) (x+1)^4 F(x)=−1 f =lim_(x→−(1/2)) (2x+1)^2 F(x)=((−1)/2).16 =−8 ⇒ F(x)=(a/(x+1)) +(b/((x+1)^2 )) +(c/((x+1)^3 )) −(1/((x+1)^4 )) +(e/(2x+1)) −(8/((2x+1)^2 )) lim_(x→+∞) xF(x)=0 =a+(e/2) ⇒2a+e=0 ⇒e=−2a ⇒F(x)=(a/(x+1)) +(b/((x+1)^2 )) +(c/((x+1)^3 )) −(1/((x+1)^4 )) −((2a)/(2x+1)) −(8/((2x+1)^2 )) F(0)=0=a+b+c−1−2a−8=−a+b+c−9 ⇒ −a+b+c =9 ⇒a−b−c=−9 F(−2)=((−2)/9) =−a+b−c−1+(2/3)a−(8/9) ⇒ −2 =−9a+9b−9c−9+6a−8 ⇒ −3a+9b−9c−15=0 ⇒3a−9b+9c+15=0 ⇒ a−3b+3c=−5...be continued...
letdecomposeF(x)=x(x+1)4(2x+1)2F(x)=ax+1+b(x+1)2+c(x+1)3+d(x+1)4+e2x+1+f(2x+1)2d=limx→−1(x+1)4F(x)=−1f=limx→−12(2x+1)2F(x)=−12.16=−8⇒F(x)=ax+1+b(x+1)2+c(x+1)3−1(x+1)4+e2x+1−8(2x+1)2limx→+∞xF(x)=0=a+e2⇒2a+e=0⇒e=−2a⇒F(x)=ax+1+b(x+1)2+c(x+1)3−1(x+1)4−2a2x+1−8(2x+1)2F(0)=0=a+b+c−1−2a−8=−a+b+c−9⇒−a+b+c=9⇒a−b−c=−9F(−2)=−29=−a+b−c−1+23a−89⇒−2=−9a+9b−9c−9+6a−8⇒−3a+9b−9c−15=0⇒3a−9b+9c+15=0⇒a−3b+3c=−5…becontinued…

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *