Question Number 55276 by maxmathsup by imad last updated on 20/Feb/19
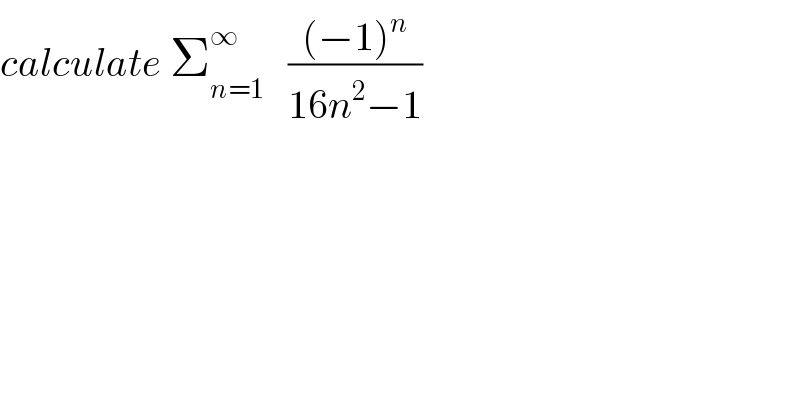
$${calculate}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{16}{n}^{\mathrm{2}} −\mathrm{1}} \\ $$
Commented by maxmathsup by imad last updated on 08/Apr/19
![let S =Σ_(n=1) ^∞ (((−1)^n )/(16n^2 −1)) ⇒S =Σ_(n=1) ^∞ (((−1)^n )/((4n−1)(4n+1))) =(1/2)Σ_(n=1) ^∞ (−1)^n { (1/(4n−1)) −(1/(4n+1))} ⇒2S =Σ_(n=1) ^∞ (((−1)^n )/(4n−1)) −Σ_(n=1) ^∞ (((−1)^n )/(4n+1)) we have proved that Σ_(n=0) ^∞ (((−1)^n )/(4n+3)) =(π/(4(√2))) (Q55268) ⇒ Σ_(n=1) ^∞ (((−1)^n )/(4n−1)) =_(n=p+1) Σ_(p=0) ^∞ (((−1)^(p+1) )/(4p+3)) =−Σ_(p=0) ^∞ (((−1)^p )/(4p+3)) =−(π/(4(√2))) let determine Σ_(n=1) ^∞ (((−1)^n )/(4n+1)) let w(x) =Σ_(n=0) ^∞ (−1)^n (x^(4n+1) /(4n+1)) with x∈[−1,1] we have w(1) =Σ_(n=0) ^∞ (((−1)^n )/(4n+1)) =1+Σ_(n=1) ^∞ (((−1)^n )/(4n+1)) ⇒Σ_(n=1) ^∞ (((−1)^n )/(4n+1)) =w(1)−1 we have w^′ (x) =Σ_(n=0) ^∞ (−1)^n x^(4n) =(1/(1+x^4 )) ⇒w(x) =∫_0 ^x (dt/(1+t^4 )) +c c=w(0) =0 ⇒w(x)=∫_0 ^x (dt/(1+t^4 )) and w(1) =∫_0 ^1 (dt/(1+t^4 )) we have ∫_0 ^∞ (dt/(1+t^4 )) =∫_0 ^1 (dt/(1+t^4 )) +∫_1 ^(+∞) (dt/(1+t^4 )) but ∫_1 ^(+∞) (dt/(1+t^4 )) =_(t =(1/x)) −∫_0 ^1 (1/(1+(1/x^4 ))) (−(dx/x^2 )) = ∫_0 ^1 (x^4 /(x^2 (1+x^4 ))) dx =∫_0 ^1 (x^2 /(1+x^4 )) dx =(π/(4(√2))) (result proved) ⇒ ∫_0 ^1 (dt/(1+t^4 )) =∫_0 ^∞ (dt/(1+t^4 )) −(π/(4(√2))) and ∫_0 ^∞ (dt/(1+t^4 )) =_(t =u^(1/4) ) ∫_0 ^∞ (1/(1+u)) (1/4)u^((1/4)−1) du =(1/4) ∫_0 ^∞ (u^((1/4)−1) /(1+u)) du =(1/4) (π/(sin((π/4)))) =(π/(4(1/( (√2))))) =((π(√2))/4) ⇒∫_0 ^1 (dt/(1+t^4 )) =((π(√2))/4) −(π/(4(√2))) =((π(√2))/4) −((π(√2))/8) =((π(√2))/8) ⇒Σ_(n=1) ^∞ (((−1)^n )/(4n+1)) =((π(√2))/8) −1 ⇒ S =(1/2){−(π/(4(√2))) −((π(√2))/8) +1} =(1/2){1−((π(√2))/4)} .](https://www.tinkutara.com/question/Q57588.png)
$${let}\:{S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{16}{n}^{\mathrm{2}} \:−\mathrm{1}}\:\Rightarrow{S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{4}{n}−\mathrm{1}\right)\left(\mathrm{4}{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \left\{\:\frac{\mathrm{1}}{\mathrm{4}{n}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{4}{n}+\mathrm{1}}\right\}\:\Rightarrow\mathrm{2}{S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}−\mathrm{1}}\:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}+\mathrm{1}} \\ $$$${we}\:{have}\:{proved}\:{that}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}+\mathrm{3}}\:=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:\:\left({Q}\mathrm{55268}\right)\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}−\mathrm{1}}\:=_{{n}={p}+\mathrm{1}} \:\:\:\sum_{{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{p}+\mathrm{1}} }{\mathrm{4}{p}+\mathrm{3}}\:=−\sum_{{p}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{p}} }{\mathrm{4}{p}+\mathrm{3}}\:=−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$${let}\:{determine}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}+\mathrm{1}}\:\:{let}\:{w}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:\:\frac{{x}^{\mathrm{4}{n}+\mathrm{1}} }{\mathrm{4}{n}+\mathrm{1}}\:\:{with}\:{x}\in\left[−\mathrm{1},\mathrm{1}\right] \\ $$$${we}\:{have}\:{w}\left(\mathrm{1}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}+\mathrm{1}}\:=\mathrm{1}+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}+\mathrm{1}}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}+\mathrm{1}}\:={w}\left(\mathrm{1}\right)−\mathrm{1} \\ $$$${we}\:{have}\:{w}^{'} \left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{4}{n}} \:=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{4}} }\:\Rightarrow{w}\left({x}\right)\:=\int_{\mathrm{0}} ^{{x}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:+{c} \\ $$$${c}={w}\left(\mathrm{0}\right)\:=\mathrm{0}\:\Rightarrow{w}\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:\:{and}\:{w}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} } \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:+\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:\:{but}\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=_{{t}\:=\frac{\mathrm{1}}{{x}}} \:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }}\:\left(−\frac{{dx}}{{x}^{\mathrm{2}} }\right) \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{\mathrm{4}} }{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{4}} \right)}\:{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx}\:\:=\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:\left({result}\:{proved}\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:\:{and}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=_{{t}\:={u}^{\frac{\mathrm{1}}{\mathrm{4}}} } \:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{u}}\:\frac{\mathrm{1}}{\mathrm{4}}{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} {du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} }{\mathrm{1}+{u}}\:{du}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{4}}\right)}\:=\frac{\pi}{\mathrm{4}\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{4}} }\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$$$=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\:−\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}+\mathrm{1}}\:=\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}}\:−\mathrm{1}\:\Rightarrow \\ $$$${S}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{−\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:−\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{8}}\:+\mathrm{1}\right\}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{1}−\frac{\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\right\}\:. \\ $$
