Menu Close

calculate-n-1-1-n-n-3-n-1-

Tinku Tara 0 Comments
Pin




Question Number 57529 by maxmathsup by imad last updated on 06/Apr/19
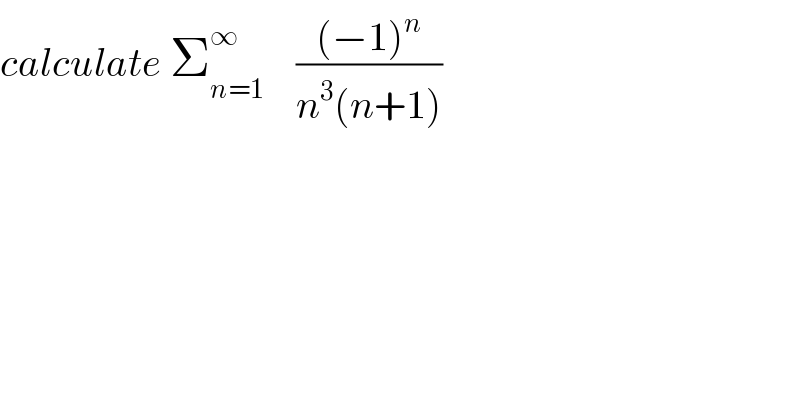
calculate Σ_(n=1) ^∞ (((−1)^n )/(n^3 (n+1)))
$${calculate}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{3}} \left({n}+\mathrm{1}\right)} \\ $$
Commented by maxmathsup by imad last updated on 09/Apr/19
let decompose F(x)=(1/((x+1)x^3 )) ⇒F(x)=(a/(x+1)) +(b/x) +(c/x^2 ) +(d/x^3 ) a =lim_(x→−1) (x+1)F(x)=−1 d =lim_(x→0) x^3 F(x) =1 ⇒F(x) =((−1)/(x+1)) +(b/x) +(c/x^2 ) +(1/x^3 ) F(1) =(1/2) =−(1/2) +b+c +1 ⇒b+c =0 ⇒c=−b F(−2) =(1/8) =1 −(b/2) +(c/4)−(1/8) ⇒1 =8−4b +2c−1 ⇒−6 =−4b +2c ⇒−3 =−2b +c b =1 and c =−1 ⇒F(x) =−(1/(x+1)) +(1/x) −(1/x^2 ) +(1/x^3 ) ⇒ Σ_(n=1) ^∞ (((−1)^n )/((n+1)n^3 )) =−Σ_(n=1) ^∞ (((−1)^n )/(n+1)) +Σ_(n=1) ^∞ (((−1)^n )/n) − Σ_(n=1) ^∞ (((−1)^n )/n^2 ) +Σ_(n=1) ^∞ (((−1)^n )/n^3 ) Σ_(n=1) ^∞ (((−1)^n )/(n+1)) =Σ_(n=2) ^∞ (((−1)^(n−1) )/n) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) −1 =ln(2)−1 Σ_(n=1) ^∞ (((−1)^n )/n) =−ln(2) let δ(x) =Σ_(n=1) ^∞ (((−1)^n )/n^x ) let determine δ(x) interms of ξ(x) (x>1) we have δ(x) =Σ_(n=1) ^∞ (1/(2^x n^x )) −Σ_(n=0) ^∞ (1/((2n+1)^x )) and Σ_(n=1) ^∞ (1/n^x ) =Σ_(n=1) ^∞ (1/(2^x n^x )) +Σ_(n=0) ^∞ (1/((2n+1)^x )) ⇒Σ_(n=0) ^∞ (1/((2n+1)^x )) =ξ(x)−2^(−x) ξ(x) =(1−2^(−x) )ξ(x) ⇒δ(x) =2^(−x) ξ(x)−(1−2^(−x) )ξ(x)=(2^(−x) −1−2^(−x) )ξ(x) =(2^(1−x) −1)ξ(x) ⇒ δ(x)=(2^(1−x) −1)ξ(x) ⇒ Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =δ(2) =(2^(1−2) −1)ξ(2) =((1/2)−1)(π^2 /6) =−(π^2 /(12)) ⇒ Σ_(n=1) ^∞ (((−1)^n )/n^3 ) =δ(3) =(2^(1−3) −1)ξ(3) =((1/4)−1)ξ(3)=−(3/4)ξ(3) Σ_(n=1) ^∞ (((−1)^n )/((n+1)n^3 )) =1−ln(2) −ln(2) −(−(π^2 /(12)))−(3/4)ξ(3) =1−2ln(2)+(π^2 /(12)) −(3/4) ξ(3) with ξ(3) =Σ_(n=1) ^∞ (1/n^3 ) .
$${let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right){x}^{\mathrm{3}} }\:\Rightarrow{F}\left({x}\right)=\frac{{a}}{{x}+\mathrm{1}}\:+\frac{{b}}{{x}}\:+\frac{{c}}{{x}^{\mathrm{2}} }\:+\frac{{d}}{{x}^{\mathrm{3}} } \\ $$$${a}\:={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)=−\mathrm{1} \\ $$$${d}\:={lim}_{{x}\rightarrow\mathrm{0}} \:{x}^{\mathrm{3}} \:{F}\left({x}\right)\:=\mathrm{1}\:\Rightarrow{F}\left({x}\right)\:=\frac{−\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{{b}}{{x}}\:+\frac{{c}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{x}^{\mathrm{3}} } \\ $$$${F}\left(\mathrm{1}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:+{b}+{c}\:+\mathrm{1}\:\Rightarrow{b}+{c}\:=\mathrm{0}\:\Rightarrow{c}=−{b} \\ $$$${F}\left(−\mathrm{2}\right)\:=\frac{\mathrm{1}}{\mathrm{8}}\:=\mathrm{1}\:−\frac{{b}}{\mathrm{2}}\:+\frac{{c}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow\mathrm{1}\:=\mathrm{8}−\mathrm{4}{b}\:+\mathrm{2}{c}−\mathrm{1}\:\Rightarrow−\mathrm{6}\:=−\mathrm{4}{b}\:+\mathrm{2}{c}\:\Rightarrow−\mathrm{3}\:=−\mathrm{2}{b}\:+{c} \\ $$$${b}\:=\mathrm{1}\:\:\:\:\:{and}\:{c}\:=−\mathrm{1}\:\Rightarrow{F}\left({x}\right)\:=−\frac{\mathrm{1}}{{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{{x}}\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right){n}^{\mathrm{3}} }\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:−\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{3}} } \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:=\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:−\mathrm{1}\:={ln}\left(\mathrm{2}\right)−\mathrm{1} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:=−{ln}\left(\mathrm{2}\right) \\ $$$${let}\:\delta\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{{x}} }\:\:{let}\:{determine}\:\delta\left({x}\right)\:{interms}\:{of}\:\xi\left({x}\right)\:\:\:\:\left({x}>\mathrm{1}\right) \\ $$$${we}\:{have}\:\delta\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{2}^{{x}} \:{n}^{{x}} }\:−\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{x}} }\:{and} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}^{{x}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{2}^{{x}} {n}^{{x}} }\:+\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{x}} }\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{{x}} }\:=\xi\left({x}\right)−\mathrm{2}^{−{x}} \xi\left({x}\right) \\ $$$$=\left(\mathrm{1}−\mathrm{2}^{−{x}} \right)\xi\left({x}\right)\:\Rightarrow\delta\left({x}\right)\:=\mathrm{2}^{−{x}} \xi\left({x}\right)−\left(\mathrm{1}−\mathrm{2}^{−{x}} \right)\xi\left({x}\right)=\left(\mathrm{2}^{−{x}} −\mathrm{1}−\mathrm{2}^{−{x}} \right)\xi\left({x}\right) \\ $$$$=\left(\mathrm{2}^{\mathrm{1}−{x}} −\mathrm{1}\right)\xi\left({x}\right)\:\Rightarrow\:\delta\left({x}\right)=\left(\mathrm{2}^{\mathrm{1}−{x}} −\mathrm{1}\right)\xi\left({x}\right)\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\:=\delta\left(\mathrm{2}\right)\:=\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)\:=\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{3}} }\:=\delta\left(\mathrm{3}\right)\:=\left(\mathrm{2}^{\mathrm{1}−\mathrm{3}} −\mathrm{1}\right)\xi\left(\mathrm{3}\right)\:=\left(\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}\right)\xi\left(\mathrm{3}\right)=−\frac{\mathrm{3}}{\mathrm{4}}\xi\left(\mathrm{3}\right) \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right){n}^{\mathrm{3}} }\:=\mathrm{1}−{ln}\left(\mathrm{2}\right)\:−{ln}\left(\mathrm{2}\right)\:−\left(−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\right)−\frac{\mathrm{3}}{\mathrm{4}}\xi\left(\mathrm{3}\right) \\ $$$$=\mathrm{1}−\mathrm{2}{ln}\left(\mathrm{2}\right)+\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\:−\frac{\mathrm{3}}{\mathrm{4}}\:\xi\left(\mathrm{3}\right)\:{with}\:\xi\left(\mathrm{3}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *