Menu Close

calculate-n-1-1-n-n-4n-2-1-

Tinku Tara 0 Comments
Pin




Question Number 52305 by Abdo msup. last updated on 05/Jan/19
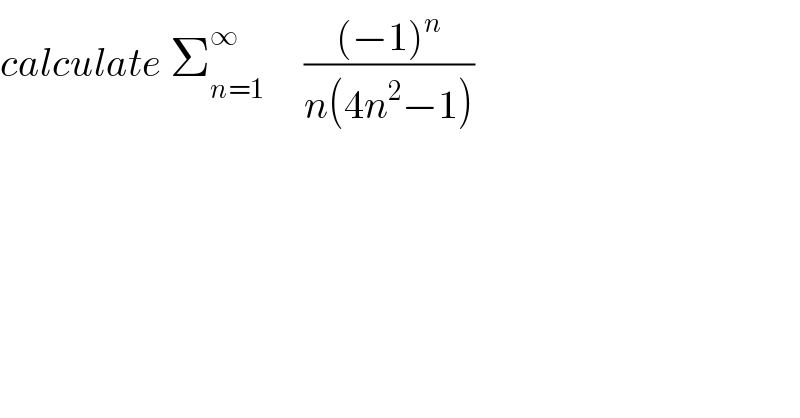
calculate Σ_(n=1) ^∞ (((−1)^n )/(n(4n^2 −1)))
$${calculate}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$
Commented by Abdo msup. last updated on 06/Jan/19
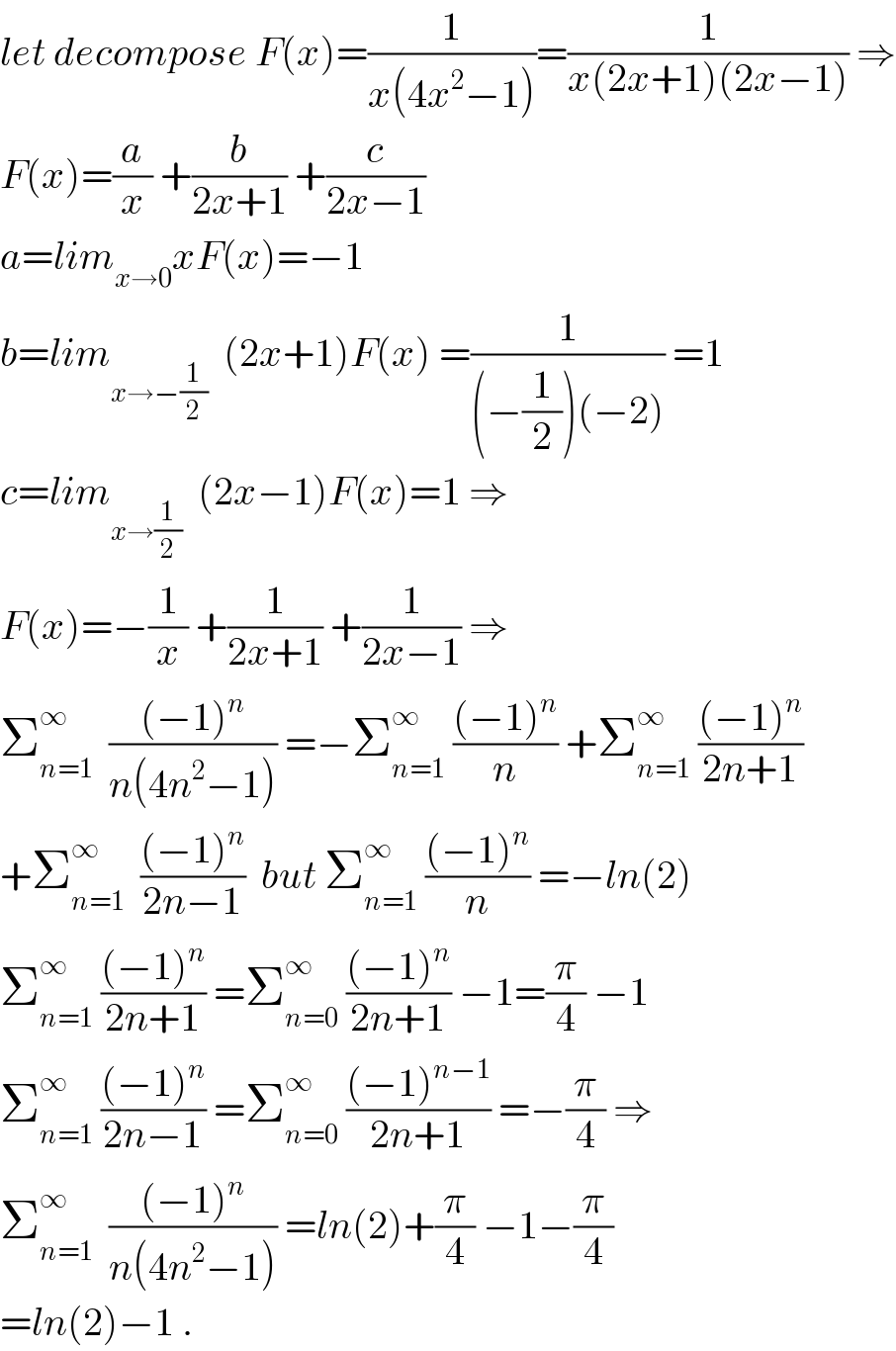
let decompose F(x)=(1/(x(4x^2 −1)))=(1/(x(2x+1)(2x−1))) ⇒ F(x)=(a/x) +(b/(2x+1)) +(c/(2x−1)) a=lim_(x→0) xF(x)=−1 b=lim_(x→−(1/2)) (2x+1)F(x) =(1/((−(1/2))(−2))) =1 c=lim_(x→(1/2)) (2x−1)F(x)=1 ⇒ F(x)=−(1/x) +(1/(2x+1)) +(1/(2x−1)) ⇒ Σ_(n=1) ^∞ (((−1)^n )/(n(4n^2 −1))) =−Σ_(n=1) ^∞ (((−1)^n )/n) +Σ_(n=1) ^∞ (((−1)^n )/(2n+1)) +Σ_(n=1) ^∞ (((−1)^n )/(2n−1)) but Σ_(n=1) ^∞ (((−1)^n )/n) =−ln(2) Σ_(n=1) ^∞ (((−1)^n )/(2n+1)) =Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) −1=(π/4) −1 Σ_(n=1) ^∞ (((−1)^n )/(2n−1)) =Σ_(n=0) ^∞ (((−1)^(n−1) )/(2n+1)) =−(π/4) ⇒ Σ_(n=1) ^∞ (((−1)^n )/(n(4n^2 −1))) =ln(2)+(π/4) −1−(π/4) =ln(2)−1 .
$${let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{{x}\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{\mathrm{1}}{{x}\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}−\mathrm{1}\right)}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}}\:+\frac{{b}}{\mathrm{2}{x}+\mathrm{1}}\:+\frac{{c}}{\mathrm{2}{x}−\mathrm{1}} \\ $$$${a}={lim}_{{x}\rightarrow\mathrm{0}} {xF}\left({x}\right)=−\mathrm{1} \\ $$$${b}={lim}_{{x}\rightarrow−\frac{\mathrm{1}}{\mathrm{2}}} \:\:\left(\mathrm{2}{x}+\mathrm{1}\right){F}\left({x}\right)\:=\frac{\mathrm{1}}{\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(−\mathrm{2}\right)}\:=\mathrm{1} \\ $$$${c}={lim}_{{x}\rightarrow\frac{\mathrm{1}}{\mathrm{2}}} \:\:\left(\mathrm{2}{x}−\mathrm{1}\right){F}\left({x}\right)=\mathrm{1}\:\Rightarrow \\ $$$${F}\left({x}\right)=−\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{1}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}} \\ $$$$+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}−\mathrm{1}}\:\:{but}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:=−{ln}\left(\mathrm{2}\right) \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:−\mathrm{1}=\frac{\pi}{\mathrm{4}}\:−\mathrm{1} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}−\mathrm{1}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\:=−\frac{\pi}{\mathrm{4}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)}\:={ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{4}}\:−\mathrm{1}−\frac{\pi}{\mathrm{4}} \\ $$$$={ln}\left(\mathrm{2}\right)−\mathrm{1}\:. \\ $$
Answered by Smail last updated on 06/Jan/19
Σ_(n=1) ^∞ (((−1)^n )/(n(4n^2 −1)))=Σ_(n=1) ^∞ (((−1)^n )/(n(2n+1)(2n−1))) (1/(n(2n+1)(2n−1)))=(a/n)+(b/(2n+1))+(c/(2n−1)) a=−1 , b=1 , c=1 Σ_(n=1) ^∞ (((−1)^n )/(n(4n^2 −1)))=Σ_(n=1) ^∞ (((−1)^n )/(2n+1))+Σ_(n=1) ^∞ (((−1)^n )/(2n−1))−Σ_(n=1) ^∞ (((−1)^n )/n) let put p(x)=Σ_(n=1) ^∞ (((−1)^n )/(2n+1))x^(2n+1) +Σ_(n=1) ^∞ (((−1)^n )/(2n−1))x^(2n−1) +Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n =Σ_(n=1) ^∞ (((−1)^n )/(2n+1))x^(2n+1) +Σ_(n=0) ^∞ (((−1)^(n−1) )/(2n+1))x^(2n+1) +Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n =Σ_(n=1) ^∞ (((−1)^n )/(2n+1))x^(2n+1) −Σ_(n=0) ^∞ (((−1)^n )/(2n+1))x^(2n+1) +Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n =−x+ln(1+x) with ∣x∣≤1 p(1)=ln(2)−1 Which means Σ_(n=1) ^∞ (((−1)^n )/(n(4n^2 −1)))=ln(2)−1
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}−\mathrm{1}\right)}=\frac{{a}}{{n}}+\frac{{b}}{\mathrm{2}{n}+\mathrm{1}}+\frac{{c}}{\mathrm{2}{n}−\mathrm{1}} \\ $$$${a}=−\mathrm{1}\:,\:\:{b}=\mathrm{1}\:,\:{c}=\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}−\mathrm{1}}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}} \\ $$$${let}\:{put}\: \\ $$$${p}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} +\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}−\mathrm{1}}{x}^{\mathrm{2}{n}−\mathrm{1}} +\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} +\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} +\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} −\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} +\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}} \\ $$$$=−{x}+{ln}\left(\mathrm{1}+{x}\right)\:{with}\:\:\mid{x}\mid\leqslant\mathrm{1} \\ $$$${p}\left(\mathrm{1}\right)={ln}\left(\mathrm{2}\right)−\mathrm{1} \\ $$$${Which}\:{means}\: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)}={ln}\left(\mathrm{2}\right)−\mathrm{1} \\ $$
Commented by Abdo msup. last updated on 06/Jan/19
thanks sir Smail.
$${thanks}\:{sir}\:{Smail}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *