Question Number 41407 by maxmathsup by imad last updated on 06/Aug/18
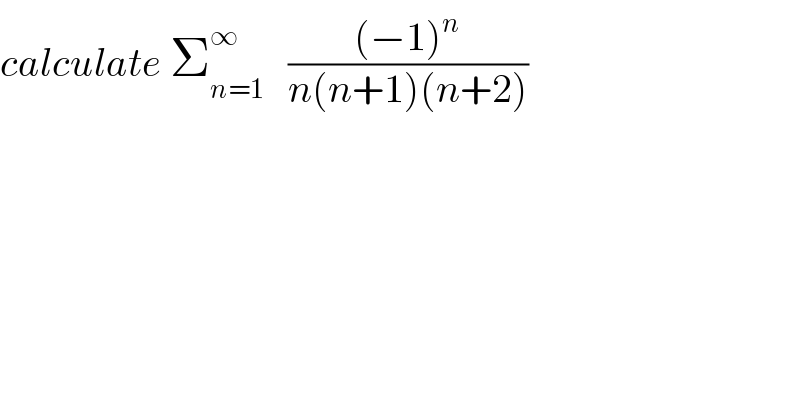
$${calculate}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$
Commented by maxmathsup by imad last updated on 08/Aug/18
![let f(x)= Σ_(n=1) ^∞ (((−1)^n )/(n(n+1)(n+2))) x^(n+2) with ∣x∣<1 we have f^′ (x)=Σ_(n=1) ^∞ (((−1)^n )/(n(n+1))) x^(n+1) =Σ_(n=1) ^∞ (−1)^n {(1/n) −(1/(n+1))}x^(n+1) =Σ_(n=1) ^∞ (((−1)^n )/n) x^(n+1) −Σ_(n=1) ^∞ (((−1)^n )/(n+1)) x^(n+1) but Σ_(n=1) ^∞ (((−1)^n )/n) x^(n+1) =−x Σ_(n=1) ^∞ (((−1)^(n−1) )/n) x^n =−xln(1+x) Σ_(n=1) ^∞ (((−1)^n )/(n+1)) x^(n+1) = Σ_(n=2) ^∞ (((−1)^(n−1) )/n) x^n =ln(1+x)−1 ⇒ f^′ (x)=−xln(1+x)−ln(1+x) +1 ⇒f(x)= ∫_0 ^x {−(t+1)ln(1+t) +1}dt +c c=f(o)=0 ⇒ f(x)=x− ∫_0 ^x (t+1)ln(t+1)dt but ∫_0 ^x (t+1)ln(t+1)dt[=_(t+1 =u) ∫_1 ^(x+1) u ln(u)du =[(u^2 /2)ln(u)]_1 ^(x+1) −∫_1 ^(x+1) (u/2) du = (((x+1)^2 )/2)ln(x+1) −(1/4)[u^2 ]_1 ^(x+1) =(((x+1)^2 )/2)ln(x+1)−(1/4)(x+1)^2 +(1/4) ⇒ f(x)=x −(((x+1)^2 )/2)ln(x+1) +(((x+1)^2 )/4) −(1/4) S=f(1) =1−2ln(2) +1−(1/4) =−2ln(2) +2−(1/4) S =−2ln(2) +(7/4)](https://www.tinkutara.com/question/Q41475.png)
$$ \\ $$$${let}\:{f}\left({x}\right)=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\:{x}^{{n}+\mathrm{2}} \:\:{with}\:\mid{x}\mid<\mathrm{1}\:\:{we}\:{have}\: \\ $$$${f}^{'} \left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}\left({n}+\mathrm{1}\right)}\:{x}^{{n}+\mathrm{1}} \:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \left\{\frac{\mathrm{1}}{{n}}\:−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right\}{x}^{{n}+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:{x}^{{n}+\mathrm{1}} \:−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:{x}^{{n}+\mathrm{1}} \:{but} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:{x}^{{n}+\mathrm{1}} \:=−{x}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{x}^{{n}} \:=−{xln}\left(\mathrm{1}+{x}\right) \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\:{x}^{{n}+\mathrm{1}} \:=\:\sum_{{n}=\mathrm{2}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{x}^{{n}} \:={ln}\left(\mathrm{1}+{x}\right)−\mathrm{1}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=−{xln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}+{x}\right)\:+\mathrm{1}\:\Rightarrow{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{{x}} \left\{−\left({t}+\mathrm{1}\right){ln}\left(\mathrm{1}+{t}\right)\:+\mathrm{1}\right\}{dt}\:+{c} \\ $$$${c}={f}\left({o}\right)=\mathrm{0}\:\Rightarrow\:{f}\left({x}\right)={x}−\:\int_{\mathrm{0}} ^{{x}} \left({t}+\mathrm{1}\right){ln}\left({t}+\mathrm{1}\right){dt}\:{but} \\ $$$$\int_{\mathrm{0}} ^{{x}} \left({t}+\mathrm{1}\right){ln}\left({t}+\mathrm{1}\right){dt}\left[=_{{t}+\mathrm{1}\:={u}} \:\:\:\int_{\mathrm{1}} ^{{x}+\mathrm{1}} \:{u}\:{ln}\left({u}\right){du}\right. \\ $$$$=\left[\frac{{u}^{\mathrm{2}} }{\mathrm{2}}{ln}\left({u}\right)\right]_{\mathrm{1}} ^{{x}+\mathrm{1}} \:−\int_{\mathrm{1}} ^{{x}+\mathrm{1}} \:\frac{{u}}{\mathrm{2}}\:{du}\:=\:\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}{ln}\left({x}+\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{4}}\left[{u}^{\mathrm{2}} \right]_{\mathrm{1}} ^{{x}+\mathrm{1}} \\ $$$$=\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}{ln}\left({x}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{4}}\left({x}+\mathrm{1}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${f}\left({x}\right)={x}\:−\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}{ln}\left({x}+\mathrm{1}\right)\:+\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${S}={f}\left(\mathrm{1}\right)\:=\mathrm{1}−\mathrm{2}{ln}\left(\mathrm{2}\right)\:+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\:=−\mathrm{2}{ln}\left(\mathrm{2}\right)\:+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${S}\:=−\mathrm{2}{ln}\left(\mathrm{2}\right)\:+\frac{\mathrm{7}}{\mathrm{4}} \\ $$
