Question Number 32998 by abdo imad last updated on 09/Apr/18
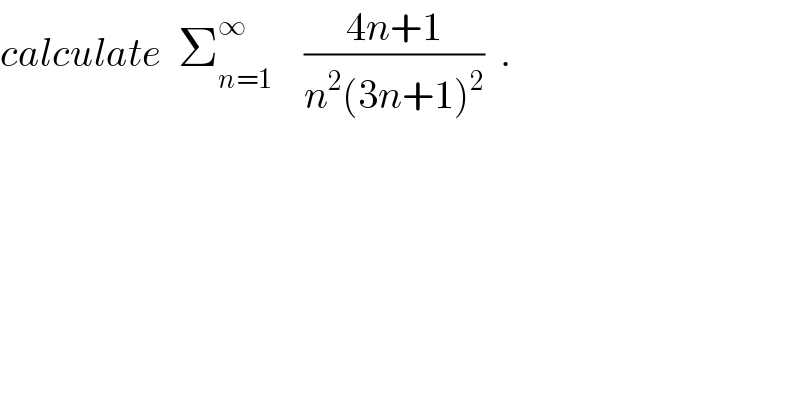
$${calculate}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\mathrm{4}{n}+\mathrm{1}}{{n}^{\mathrm{2}} \left(\mathrm{3}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\:. \\ $$
Commented by abdo imad last updated on 15/Apr/18
![let decompose F(x)= ((4x+1)/(x^2 (3x+1)^2 )) F(x) = (a/x) +(b/x^2 ) + (c/(3x+1)) +(d/((3x+1)^2 )) b =lim_(x→0) x^2 F(x)= 1 d=lim_(x→−(1/3)) (3x+1)^2 F(x) = ((−(4/3)+1)/(1/9)) =9.(−(1/3))=−3 F(x)= (a/x) +(1/x^2 ) +(c/(3x+1)) −(3/((3x+1)^2 )) lim_(x→∞) xF(x)= 0 = a+c ⇒c=−a ⇒ F(x)= (a/x) +(1/x^2 ) −(a/(3x+1)) −(3/((3x+1)^2 )) F(1) = (5/(16)) = a +1 −(a/4) −(3/(16)) =(3/4)a +((13)/(16)) ⇒ 5=12a +13⇒12a=5−13=−8 ⇒a=−(8/(12)) =−(2/3) F(x) = ((−2)/(3x)) +(1/x^2 ) + (2/(3(3x+1))) −(3/((3x+1)^2 )) Σ_(k=1) ^n ((4k+1)/(k^2 (3k+1)^2 )) =−(2/3) Σ_(k=1) ^n (1/k) +Σ_(k=1) ^n (1/k^2 ) + (2/3) Σ_(k=1) ^n (1/(3k+1)) −3 Σ_(k=1) ^n (1/((3k+1)^2 )) =(2/3)Σ_(k=1) ^n ( (1/(3k+1)) −(1/k)) +Σ_(k=1) ^n (1/k^2 ) −3 Σ_(k=1) ^n (1/((3k+1)^2 )) but Σ_(k=1) ^n (1/(3k+1)) =(1/4) +(1/7) + (1/(10)) +....+(1/(3n+1)) Σ_(k=1) ^n (1/k) = Σ_(k=3p) (...) +Σ_(k=3p+1) (...) +Σ_(k=3p+2) (...) = Σ_(p=1) ^([(n/3)]) (1/(3p)) +Σ_(k=0) ^([((n−1)/3)]) (1/(3p+1)) + Σ_(p=0) ^([((n−2)/3)]) (1/(3p+2)) ...be continued...](https://www.tinkutara.com/question/Q33402.png)
$${let}\:{decompose}\:{F}\left({x}\right)=\:\frac{\mathrm{4}{x}+\mathrm{1}}{{x}^{\mathrm{2}} \left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left({x}\right)\:=\:\frac{{a}}{{x}}\:+\frac{{b}}{{x}^{\mathrm{2}} }\:\:+\:\frac{{c}}{\mathrm{3}{x}+\mathrm{1}}\:+\frac{{d}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${b}\:={lim}_{{x}\rightarrow\mathrm{0}} \:{x}^{\mathrm{2}} {F}\left({x}\right)=\:\mathrm{1} \\ $$$${d}={lim}_{{x}\rightarrow−\frac{\mathrm{1}}{\mathrm{3}}} \:\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} {F}\left({x}\right)\:=\:\frac{−\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{9}}}\:=\mathrm{9}.\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)=−\mathrm{3} \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{x}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\:+\frac{{c}}{\mathrm{3}{x}+\mathrm{1}}\:−\frac{\mathrm{3}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${lim}_{{x}\rightarrow\infty} \:{xF}\left({x}\right)=\:\mathrm{0}\:=\:{a}+{c}\:\Rightarrow{c}=−{a}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{{a}}{{x}}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\frac{{a}}{\mathrm{3}{x}+\mathrm{1}}\:−\frac{\mathrm{3}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{1}\right)\:=\:\frac{\mathrm{5}}{\mathrm{16}}\:=\:{a}\:+\mathrm{1}\:−\frac{{a}}{\mathrm{4}}\:−\frac{\mathrm{3}}{\mathrm{16}}\:=\frac{\mathrm{3}}{\mathrm{4}}{a}\:\:+\frac{\mathrm{13}}{\mathrm{16}}\:\Rightarrow \\ $$$$\mathrm{5}=\mathrm{12}{a}\:+\mathrm{13}\Rightarrow\mathrm{12}{a}=\mathrm{5}−\mathrm{13}=−\mathrm{8}\:\Rightarrow{a}=−\frac{\mathrm{8}}{\mathrm{12}}\:=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${F}\left({x}\right)\:=\:\frac{−\mathrm{2}}{\mathrm{3}{x}}\:\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:+\:\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{3}{x}+\mathrm{1}\right)}\:−\frac{\mathrm{3}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{4}{k}+\mathrm{1}}{{k}^{\mathrm{2}} \left(\mathrm{3}{k}+\mathrm{1}\right)^{\mathrm{2}} }\:=−\frac{\mathrm{2}}{\mathrm{3}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:\:+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$+\:\frac{\mathrm{2}}{\mathrm{3}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{3}{k}+\mathrm{1}}\:−\mathrm{3}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\left(\mathrm{3}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\left(\:\frac{\mathrm{1}}{\mathrm{3}{k}+\mathrm{1}}\:−\frac{\mathrm{1}}{{k}}\right)\:+\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:−\mathrm{3}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\left(\mathrm{3}{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${but}\:\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\mathrm{3}{k}+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{7}}\:+\:\frac{\mathrm{1}}{\mathrm{10}}\:+….+\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{1}} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}}\:=\:\sum_{{k}=\mathrm{3}{p}} \left(…\right)\:+\sum_{{k}=\mathrm{3}{p}+\mathrm{1}} \left(…\right)\:+\sum_{{k}=\mathrm{3}{p}+\mathrm{2}} \left(…\right) \\ $$$$=\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{3}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{3}{p}}\:\:\:+\sum_{{k}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{3}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{3}{p}+\mathrm{1}}\:+\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{2}}{\mathrm{3}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{3}{p}+\mathrm{2}}\:\:…{be}\:{continued}… \\ $$
