Question Number 45518 by maxmathsup by imad last updated on 14/Oct/18

$${calculate}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({n}\theta\right)}{{n}^{\mathrm{2}} }\:\:{and}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{sin}\left({n}\theta\right)}{{n}^{\mathrm{2}} } \\ $$
Commented by maxmathsup by imad last updated on 23/Oct/18
![we have proved that Σ_(n=1) ^∞ ((cos(nx))/n) =ln(sin((x/2))) ⇒ ∫_0 ^x (Σ_(n=1) ^∞ ((cos(nt))/n))dt =∫_0 ^x ln(sin((t/2)))dt ⇒ Σ_(n=1) ^∞ (1/n)[(1/n)sin(nt)]_0 ^x = ∫_0 ^x ln(sin((t/2)))dt⇒ Σ_(n=1) ^∞ ((sin(nx))/n^2 ) = ∫_0 ^x ln(sin((t/2)))dt=_((t/2)=u ) 2 ∫_0 ^(x/2) ln(sin(u))du also we have Σ_(n=1) ^∞ ((sin(nx))/n) =((π−x)/2) ⇒ ∫_0 ^x (Σ_(n=1) ^∞ ((sin(nt))/n))dt =∫_0 ^x ((π−t)/2)dt ⇒ Σ_(n=1) ^∞ (1/n) ∫_0 ^x sin(nt)dt =((πx)/2) −(1/2) (x^2 /2) ⇒ Σ_(n=1) ^∞ (1/n)[−(1/n)cos(nt)]_0 ^x =((πx)/2) −(x^2 /4) ⇒ Σ_(n=1) ^∞ (1/n^2 ){1−cos(nx)} =((πx)/2) −(x^2 /4) ⇒ Σ_(n=1) ^∞ ((cos(nx))/n^2 ) =(π^2 /6) −((πx)/2) +(x^2 /4) .](https://www.tinkutara.com/question/Q46318.png)
$${we}\:{have}\:{proved}\:{that}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nx}\right)}{{n}}\:={ln}\left({sin}\left(\frac{{x}}{\mathrm{2}}\right)\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{{x}} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{cos}\left({nt}\right)}{{n}}\right){dt}\:=\int_{\mathrm{0}} ^{{x}} {ln}\left({sin}\left(\frac{{t}}{\mathrm{2}}\right)\right){dt}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\left[\frac{\mathrm{1}}{{n}}{sin}\left({nt}\right)\right]_{\mathrm{0}} ^{{x}} =\:\int_{\mathrm{0}} ^{{x}} {ln}\left({sin}\left(\frac{{t}}{\mathrm{2}}\right)\right){dt}\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{{n}^{\mathrm{2}} }\:=\:\int_{\mathrm{0}} ^{{x}} {ln}\left({sin}\left(\frac{{t}}{\mathrm{2}}\right)\right){dt}=_{\frac{{t}}{\mathrm{2}}={u}\:} \:\:\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{{x}}{\mathrm{2}}} {ln}\left({sin}\left({u}\right)\right){du}\:{also}\:{we}\:{have} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{{n}}\:=\frac{\pi−{x}}{\mathrm{2}}\:\Rightarrow\:\int_{\mathrm{0}} ^{{x}} \left(\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{sin}\left({nt}\right)}{{n}}\right){dt}\:=\int_{\mathrm{0}} ^{{x}} \:\frac{\pi−{t}}{\mathrm{2}}{dt}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{{x}} \:{sin}\left({nt}\right){dt}\:=\frac{\pi{x}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\left[−\frac{\mathrm{1}}{{n}}{cos}\left({nt}\right)\right]_{\mathrm{0}} ^{{x}} \:=\frac{\pi{x}}{\mathrm{2}}\:−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\left\{\mathrm{1}−{cos}\left({nx}\right)\right\}\:=\frac{\pi{x}}{\mathrm{2}}\:−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \frac{{cos}\left({nx}\right)}{{n}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:−\frac{\pi{x}}{\mathrm{2}}\:+\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/Oct/18

$${P}_{{n}} +{iQ}_{{n}} =\frac{{cosn}\theta}{{n}^{\mathrm{2}} }+{i}\frac{{sinn}\theta}{{n}^{\mathrm{2}} }=\frac{{e}^{{in}\theta} }{{n}^{\mathrm{2}} } \\ $$$${T}_{{n}} ={P}+{iQ}_{{n}} =\frac{{e}^{{in}\theta} }{{n}^{\mathrm{2}} } \\ $$$${S}_{{n}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{T}_{{n}} \\ $$$${S}_{{n}} =\frac{{e}^{{i}\theta} }{\mathrm{1}^{\mathrm{2}} }+\frac{{e}^{{i}\mathrm{2}\theta} }{\mathrm{2}^{\mathrm{2}} }+\frac{{e}^{{i}\mathrm{3}\theta} }{\mathrm{3}^{\mathrm{2}} }+…\infty \\ $$$${S}_{{n}} =\frac{{x}}{\mathrm{1}^{\mathrm{2}} }+\frac{{x}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }+\frac{{x}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{2}} }+…\infty \\ $$$${wait}\:{plz}… \\ $$
Answered by Meritguide1234 last updated on 15/Oct/18
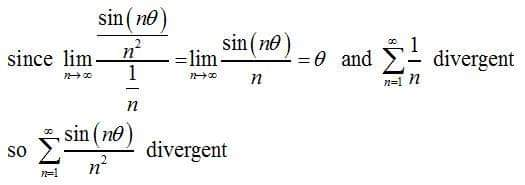
Commented by maxmathsup by imad last updated on 21/Oct/18
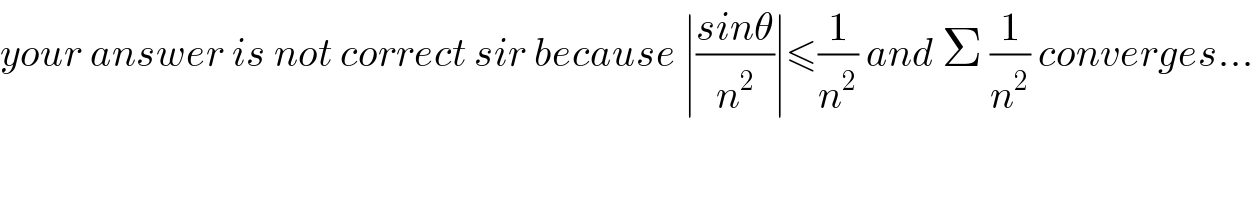
$${your}\:{answer}\:{is}\:{not}\:{correct}\:{sir}\:{because}\:\mid\frac{{sin}\theta}{{n}^{\mathrm{2}} }\mid\leqslant\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:{and}\:\Sigma\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:{converges}… \\ $$
