Question Number 45237 by maxmathsup by imad last updated on 10/Oct/18
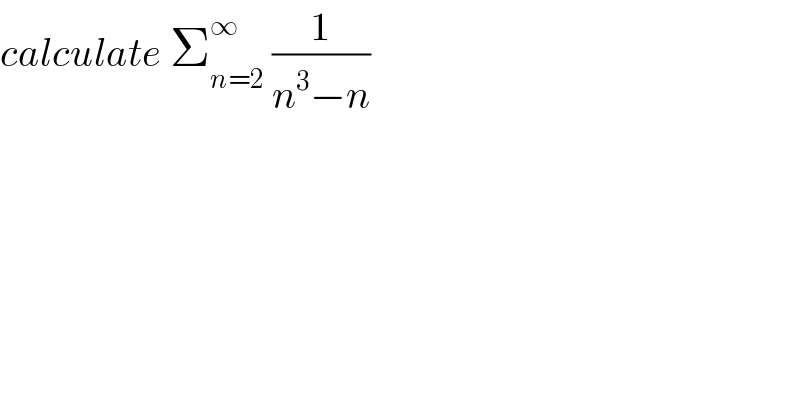
$${calculate}\:\sum_{{n}=\mathrm{2}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{3}} −{n}} \\ $$
Commented by maxmathsup by imad last updated on 11/Oct/18

$${let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{3}} −{x}}\:=\frac{\mathrm{1}}{{x}\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)} \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}}\:+\frac{{b}}{{x}−\mathrm{1}}\:+\frac{{c}}{{x}+\mathrm{1}} \\ $$$${a}\:={lim}_{{x}\rightarrow\mathrm{0}} {xF}\left({x}\right)\:=−\mathrm{1} \\ $$$${b}\:={lim}_{{x}\rightarrow\mathrm{1}} \left({x}−\mathrm{1}\right){F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${c}\:={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right){F}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{F}\left({x}\right)=−\frac{\mathrm{1}}{{x}}\:+\frac{\mathrm{1}}{\mathrm{2}\left({x}−\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{1}\right)} \\ $$$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{2}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}^{\mathrm{3}} −{k}}\:\Rightarrow{S}_{{n}} =\sum_{{k}=\mathrm{2}} ^{{n}} \:{F}\left({k}\right)\:=−\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}−\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}} \\ $$$${but}\:\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}} −\mathrm{1} \\ $$$$\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}−\mathrm{1}}\:=\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}−\mathrm{1}} \\ $$$$\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{1}}\:=\sum_{{k}=\mathrm{3}} ^{{n}+\mathrm{1}} \:\frac{\mathrm{1}}{{k}}={H}_{{n}+\mathrm{1}} −\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow{S}_{{n}} =−{H}_{{n}+\mathrm{1}} \:+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}−\mathrm{1}} +\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}+\mathrm{1}} −\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow\:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left({n}−\mathrm{1}\right)+\gamma\:+{ln}\left({n}+\mathrm{1}\right)+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\right)−{ln}\left({n}\right)−\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\:+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$={ln}\left(\sqrt{{n}−\mathrm{1}}\sqrt{{n}+\mathrm{1}}\right)−{ln}\left({n}\right)+{o}\left(\frac{\mathrm{1}}{{n}}\right)+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$={ln}\left\{\frac{\sqrt{{n}^{\mathrm{2}} −\mathrm{1}}}{{n}}\right\}+{o}\left(\frac{\mathrm{1}}{{n}}\right)+\frac{\mathrm{1}}{\mathrm{4}}\:\rightarrow\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\left({n}\rightarrow+\infty\right)\:{so}\:\:{lim}_{{n}\rightarrow+\infty} {S}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}}\:. \\ $$
Answered by Smail last updated on 11/Oct/18
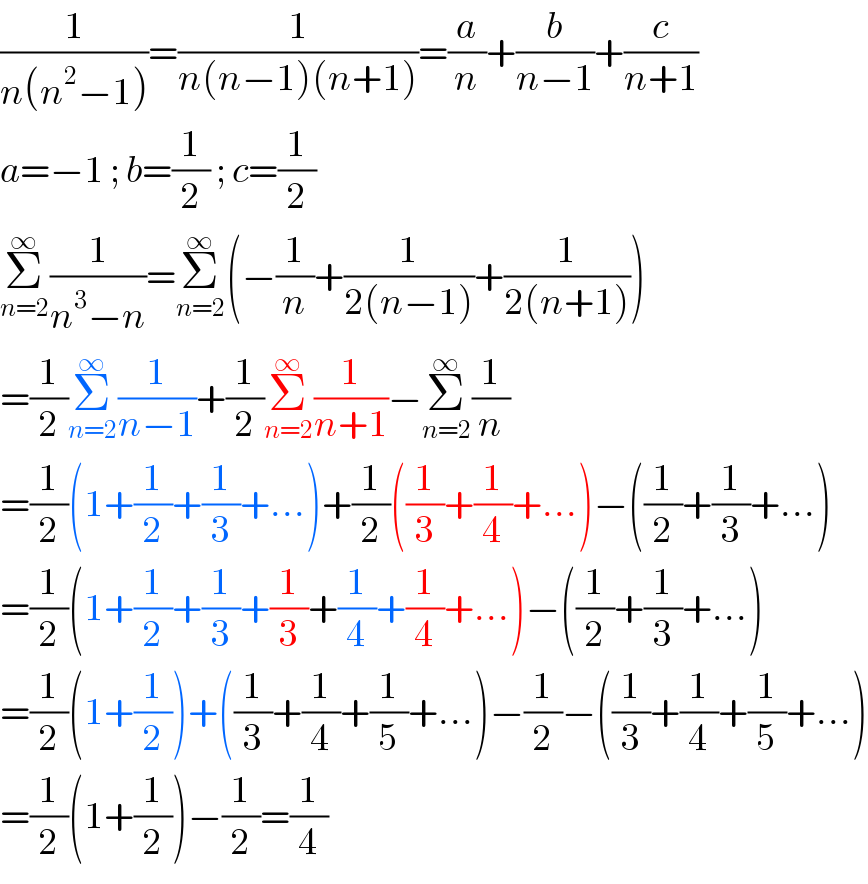
$$\frac{\mathrm{1}}{{n}\left({n}^{\mathrm{2}} −\mathrm{1}\right)}=\frac{\mathrm{1}}{{n}\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)}=\frac{{a}}{{n}}+\frac{{b}}{{n}−\mathrm{1}}+\frac{{c}}{{n}+\mathrm{1}} \\ $$$${a}=−\mathrm{1}\:;\:{b}=\frac{\mathrm{1}}{\mathrm{2}}\:;\:{c}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{3}} −{n}}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\left(−\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{\mathrm{2}\left({n}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}−\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+…\right)−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}}+…\right)−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+…\right)−\frac{\mathrm{1}}{\mathrm{2}}−\left(\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+…\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by Tawa1 last updated on 11/Oct/18

$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\:\mathrm{nth}\:\mathrm{term}\:\mathrm{of}\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}.\mathrm{2}.\mathrm{3}}\:+\:\frac{\mathrm{1}}{\mathrm{4}.\mathrm{5}.\mathrm{6}}\:+\:\frac{\mathrm{1}}{\mathrm{7}.\mathrm{8}.\mathrm{9}}\:+\:…\:\:=\:\:? \\ $$
Commented by maxmathsup by imad last updated on 11/Oct/18
$${your}\:{answer}\:{is}\:{correct}\:{sir}\:{sma}\mathrm{3}{l}\:\:{tbanks}.. \\ $$
