Menu Close

calculate-S-n-k-0-n-1-sin-pi-4n-kpi-2n-

Tinku Tara 0 Comments
Pin




Question Number 51996 by maxmathsup by imad last updated on 01/Jan/19
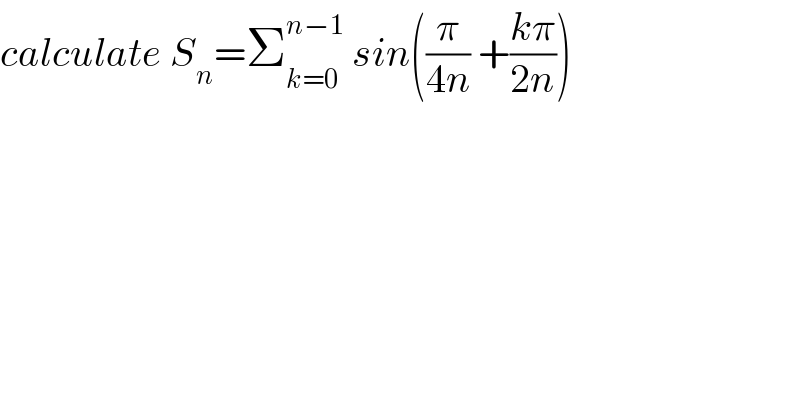
calculate S_n =Σ_(k=0) ^(n−1) sin((π/(4n)) +((kπ)/(2n)))
$${calculate}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{sin}\left(\frac{\pi}{\mathrm{4}{n}}\:+\frac{{k}\pi}{\mathrm{2}{n}}\right)\: \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 19/Jan/19
we have S_n =Σ_(k=0) ^(n−1) sin((((2k+1)π)/(4n))) =Im(Σ_(k=0) ^(n−1) e^(i((((2k+1)π)/(4n)))) ) but A_n =Σ_(k=0) ^(n−1) e^(i(((2k+1)π)/(4n))) =e^(i(π/(4n))) Σ_(k=0) ^(n−1) (e^((iπ)/(2n)) )^k =e^((iπ)/(4n)) ((1−(e^((iπ)/(2n)) )^n )/(1−e^((iπ)/(2n)) )) =e^((iπ)/(4n)) ((1−i)/(1−cos((π/(2n)))−isin((π/(2n))))) =e^((iπ)/(4n)) (((√2)e^(−((iπ)/4)) )/(2sin^2 ((π/(4n)))−2isin((π/(4n)))cos((π/(4n))))) =((√2)/2) e^((iπ)/(4n)) (e^(−((iπ)/4)) /(−isin((π/(4n)))(e^((iπ)/(4n)) ))) =i ((√2)/2) e^((iπ)/(4n)) ((e^(−((iπ)/4)) e^(−((iπ)/(4n))) )/(sin((π/(4n))))) =i((√2)/2) (((1/( (√2)))−(i/( (√2))))/(sin((π/(4n))))) =(i/2) ((1−i)/(sin((π/(4n))))) =(1/2) ((i+1)/(sin((π/(4n))))) ⇒★ S_n =(1/(2sin((π/(4n))))) ★
$${we}\:{have}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} {sin}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right) \\ $$$$={Im}\left(\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{e}^{{i}\left(\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right)} \right)\:{but}\: \\ $$$${A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{e}^{{i}\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{4}{n}}} ={e}^{{i}\frac{\pi}{\mathrm{4}{n}}} \:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\left({e}^{\frac{{i}\pi}{\mathrm{2}{n}}} \right)^{{k}} \\ $$$$={e}^{\frac{{i}\pi}{\mathrm{4}{n}}} \:\frac{\mathrm{1}−\left({e}^{\frac{{i}\pi}{\mathrm{2}{n}}} \right)^{{n}} }{\mathrm{1}−{e}^{\frac{{i}\pi}{\mathrm{2}{n}}} }\:={e}^{\frac{{i}\pi}{\mathrm{4}{n}}} \:\frac{\mathrm{1}−{i}}{\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{2}{n}}\right)−{isin}\left(\frac{\pi}{\mathrm{2}{n}}\right)} \\ $$$$={e}^{\frac{{i}\pi}{\mathrm{4}{n}}} \:\:\:\frac{\sqrt{\mathrm{2}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}{n}}\right)−\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{4}{n}}\right){cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)} \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}{n}}} \:\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} }{−{isin}\left(\frac{\pi}{\mathrm{4}{n}}\right)\left({e}^{\frac{{i}\pi}{\mathrm{4}{n}}} \right)}\: \\ $$$$={i}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}{n}}} \:\:\:\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:{e}^{−\frac{{i}\pi}{\mathrm{4}{n}}} }{{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:={i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\frac{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{{i}}{\:\sqrt{\mathrm{2}}}}{{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)} \\ $$$$=\frac{{i}}{\mathrm{2}}\:\frac{\mathrm{1}−{i}}{{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{i}+\mathrm{1}}{{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:\Rightarrow\bigstar\:{S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)}\:\bigstar \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jan/19
T_1 =sin((π/(4n)))=sin((π/(4n))) T_2 =sin((π/(4n))+(π/(2n)))=sin(((3π)/(4n))) T_3 =sin((π/(4n))+((2π)/(2n)))=sin(((5π)/(4n))) T_4 =sin((π/(4n))+((3π)/(2n)))=sin(((7π)/(4n))) ... .... T_n =sin((π/(4n))+(((n−1)π)/(2n)))=sin(((π+2(n−1)π)/(4n))) now 2sin((π/(4n)))sin((π/(4n)))=cos0−cos(((2π)/(4n))) 2sin(((3π)/(4n)))sin((π/(4n)))=cos(((2π)/(4n)))−cos(((4π)/(4n))) 2sin(((5π)/(4n)))sin((π/(4n)))=cos(((4π)/(4n)))−cos(((6π)/(4n))) .... .... 2sin(((π+2(n−1)π)/(4n)))sin((π/(4n)))=cos(((2(n−1)π)/(4n)))−cos(((2nπ)/(4n))) add them 2sin((π/(4n)))×S_n =cos0−cos(((2nπ)/(4n))) 2sin((π/(4n)))×S_n =1−cos((π/2)) S_n =(1/(2sin((π/(4n)))))
$${T}_{\mathrm{1}} ={sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)={sin}\left(\frac{\pi}{\mathrm{4}{n}}\right) \\ $$$${T}_{\mathrm{2}} ={sin}\left(\frac{\pi}{\mathrm{4}{n}}+\frac{\pi}{\mathrm{2}{n}}\right)={sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}{n}}\right) \\ $$$${T}_{\mathrm{3}} ={sin}\left(\frac{\pi}{\mathrm{4}{n}}+\frac{\mathrm{2}\pi}{\mathrm{2}{n}}\right)={sin}\left(\frac{\mathrm{5}\pi}{\mathrm{4}{n}}\right) \\ $$$${T}_{\mathrm{4}} ={sin}\left(\frac{\pi}{\mathrm{4}{n}}+\frac{\mathrm{3}\pi}{\mathrm{2}{n}}\right)={sin}\left(\frac{\mathrm{7}\pi}{\mathrm{4}{n}}\right) \\ $$$$… \\ $$$$…. \\ $$$${T}_{{n}} ={sin}\left(\frac{\pi}{\mathrm{4}{n}}+\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}{n}}\right)={sin}\left(\frac{\pi+\mathrm{2}\left({n}−\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right) \\ $$$${now} \\ $$$$\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right){sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)={cos}\mathrm{0}−{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{4}{n}}\right) \\ $$$$\mathrm{2}{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{4}{n}}\right){sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)={cos}\left(\frac{\mathrm{2}\pi}{\mathrm{4}{n}}\right)−{cos}\left(\frac{\mathrm{4}\pi}{\mathrm{4}{n}}\right) \\ $$$$\mathrm{2}{sin}\left(\frac{\mathrm{5}\pi}{\mathrm{4}{n}}\right){sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)={cos}\left(\frac{\mathrm{4}\pi}{\mathrm{4}{n}}\right)−{cos}\left(\frac{\mathrm{6}\pi}{\mathrm{4}{n}}\right) \\ $$$$…. \\ $$$$…. \\ $$$$\mathrm{2}{sin}\left(\frac{\pi+\mathrm{2}\left({n}−\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right){sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)={cos}\left(\frac{\mathrm{2}\left({n}−\mathrm{1}\right)\pi}{\mathrm{4}{n}}\right)−{cos}\left(\frac{\mathrm{2}{n}\pi}{\mathrm{4}{n}}\right) \\ $$$${add}\:{them} \\ $$$$\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)×{S}_{{n}} ={cos}\mathrm{0}−{cos}\left(\frac{\mathrm{2}{n}\pi}{\mathrm{4}{n}}\right) \\ $$$$\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)×{S}_{{n}} =\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)} \\ $$$$ \\ $$
Commented by Abdo msup. last updated on 19/Jan/19
thanks sir Tanmay.
$${thanks}\:{sir}\:{Tanmay}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *