Question Number 36741 by prof Abdo imad last updated on 04/Jun/18
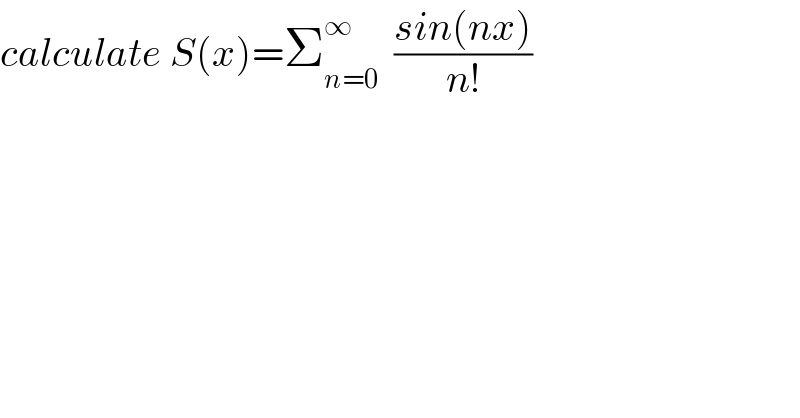
$${calculate}\:{S}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left({nx}\right)}{{n}!} \\ $$
Commented by abdo.msup.com last updated on 05/Jun/18
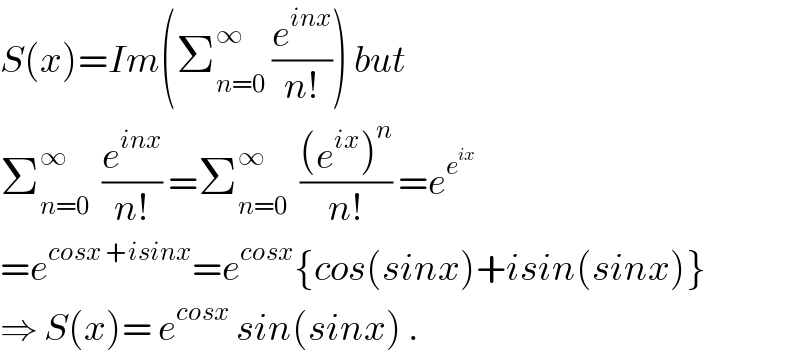
$${S}\left({x}\right)={Im}\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{e}^{{inx}} }{{n}!}\right)\:{but} \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{e}^{{inx}} }{{n}!}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left({e}^{{ix}} \right)^{{n}} }{{n}!}\:={e}^{{e}^{{ix}} } \\ $$$$={e}^{{cosx}\:+{isinx}} ={e}^{{cosx}} \left\{{cos}\left({sinx}\right)+{isin}\left({sinx}\right)\right\} \\ $$$$\Rightarrow\:{S}\left({x}\right)=\:{e}^{{cosx}} \:{sin}\left({sinx}\right)\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
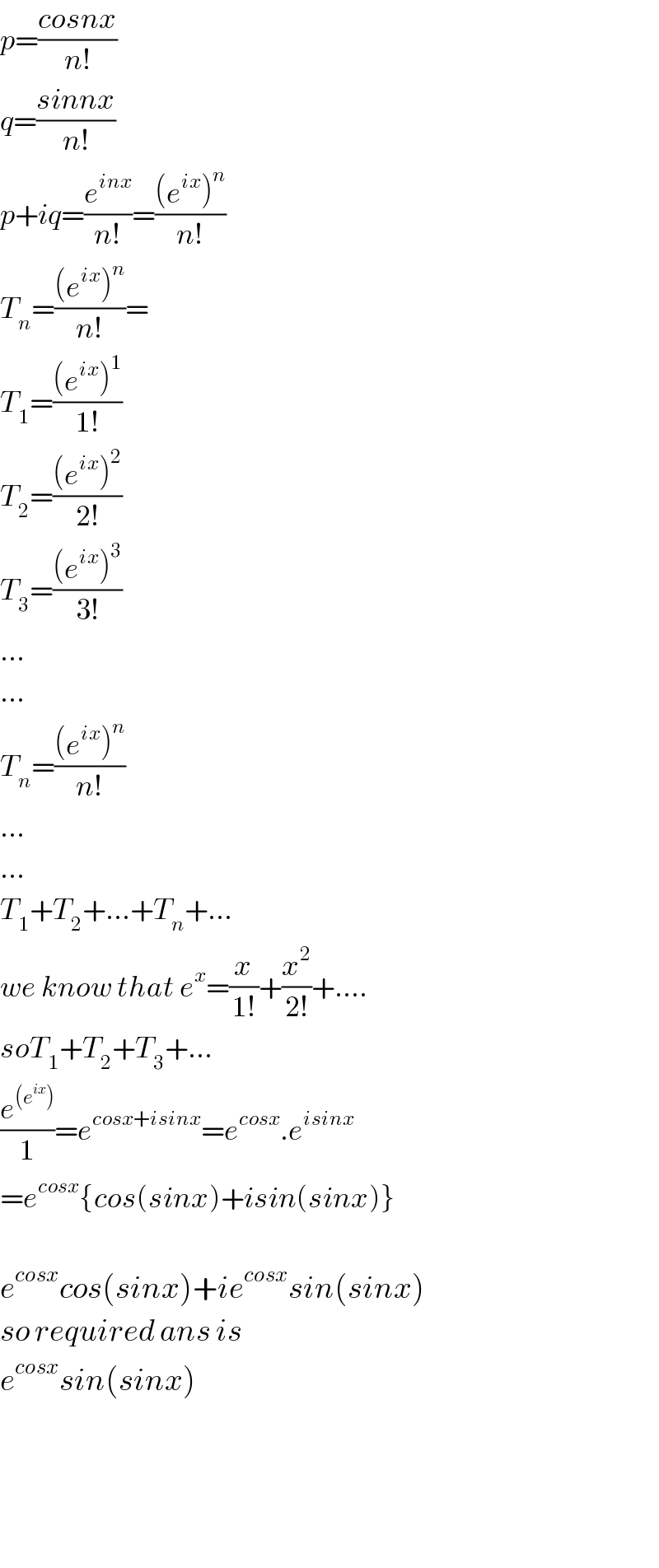
$${p}=\frac{{cosnx}}{{n}!} \\ $$$${q}=\frac{{sinnx}}{{n}!} \\ $$$${p}+{iq}=\frac{{e}^{{inx}} }{{n}!}=\frac{\left({e}^{{ix}} \right)^{{n}} }{{n}!} \\ $$$${T}_{{n}} =\frac{\left({e}^{{ix}} \right)^{{n}} }{{n}!}= \\ $$$${T}_{\mathrm{1}} =\frac{\left({e}^{{ix}} \right)^{\mathrm{1}} }{\mathrm{1}!} \\ $$$${T}_{\mathrm{2}} =\frac{\left({e}^{{ix}} \right)^{\mathrm{2}} }{\mathrm{2}!} \\ $$$${T}_{\mathrm{3}} =\frac{\left({e}^{{ix}} \right)^{\mathrm{3}} }{\mathrm{3}!} \\ $$$$… \\ $$$$… \\ $$$${T}_{{n}} =\frac{\left({e}^{{ix}} \right)^{{n}} }{{n}!} \\ $$$$… \\ $$$$… \\ $$$${T}_{\mathrm{1}} +{T}_{\mathrm{2}} +…+{T}_{{n}} +… \\ $$$${we}\:{know}\:{that}\:{e}^{{x}} =\frac{{x}}{\mathrm{1}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+…. \\ $$$${soT}_{\mathrm{1}} +{T}_{\mathrm{2}} +{T}_{\mathrm{3}} +… \\ $$$$\frac{{e}^{\left({e}^{{ix}} \right)} }{\mathrm{1}}={e}^{{cosx}+{isinx}} ={e}^{{cosx}} .{e}^{{isinx}} \\ $$$$={e}^{{cosx}} \left\{{cos}\left({sinx}\right)+{isin}\left({sinx}\right)\right\} \\ $$$$ \\ $$$${e}^{{cosx}} {cos}\left({sinx}\right)+{ie}^{{cosx}} {sin}\left({sinx}\right) \\ $$$${so}\:{required}\:{ans}\:{is}\: \\ $$$${e}^{{cosx}} {sin}\left({sinx}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
