calculate-the-area-of-one-leaf-of-r-sin-n-n-N-

Question Number 40270 by MJS last updated on 18/Jul/18

calculate the area of one “ {leaf}^{″} of

r = \sin n θ

n \in N

Answered by MrW3 last updated on 19/Jul/18

o n e l e a f m e a n s 0 ⩽ θ ⩽ \frac{π}{n}

A = \int_{0}^{\frac{π}{n}} \frac{r^{2} d θ}{2} = \frac{1}{2} \int_{0}^{\frac{π}{n}} \sin^{2} n θ d θ

= \frac{1}{4} \int_{0}^{\frac{π}{n}} (1 - \cos 2 n θ) d θ

= \frac{1}{8 n} \int_{0}^{\frac{π}{n}} (1 - \cos 2 n θ) d (2 n θ)

= \frac{1}{8 n} {[2 n θ - \sin 2 n θ]}_{0}^{\frac{π}{n}}

= \frac{π}{4 n}

Commented by MJS last updated on 19/Jul/18

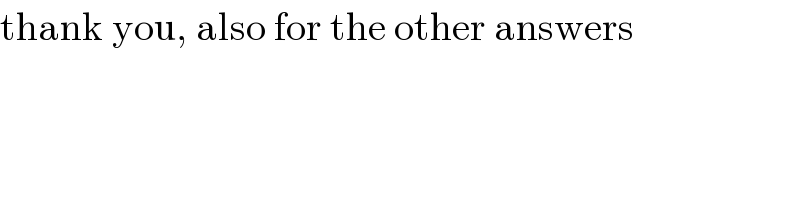
thank you, also for the other answers

Facebook Tweet Pin