Menu Close

Calculate-the-energy-loss-when-a-5-kg-object-moving-at-5-ms-1-collides-head-on-with-and-sticks-to-a-stationary-3-kg-object-Answer-3-75-J-I-need-help-How-do-I-arrive-at-this-

Tinku Tara 0 Comments
Pin




Question Number 130066 by Don08q last updated on 22/Jan/21
Calculate the energy loss when a 5 kg object moving at 5 ms^(−1) collides head −on with and sticks to a stationary 3 kg object. [Answer: 3.75 J] I need help. How do I arrive at this answer?
$$\mathrm{Calculate}\:\mathrm{the}\:\mathrm{energy}\:\mathrm{loss}\:\mathrm{when}\:\mathrm{a}\:\mathrm{5}\:{kg} \\ $$$$\mathrm{object}\:\mathrm{moving}\:\mathrm{at}\:\mathrm{5}\:{ms}^{−\mathrm{1}} \:\mathrm{collides}\:\mathrm{head} \\ $$$$−\mathrm{on}\:\mathrm{with}\:\mathrm{and}\:\mathrm{sticks}\:\mathrm{to}\:\mathrm{a}\:\mathrm{stationary} \\ $$$$\mathrm{3}\:{kg}\:\mathrm{object}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\boldsymbol{{Answer}}:\:\:\mathrm{3}.\mathrm{75}\:\mathrm{J}\right] \\ $$$$\:{I}\:{need}\:{help}.\:\mathrm{How}\:\mathrm{do}\:\mathrm{I}\:\mathrm{arrive}\:\mathrm{at}\:\mathrm{this} \\ $$$$\:\mathrm{answer}? \\ $$
Commented by mr W last updated on 22/Jan/21
answer is wrong!
$${answer}\:{is}\:{wrong}! \\ $$
Answered by ajfour last updated on 22/Jan/21
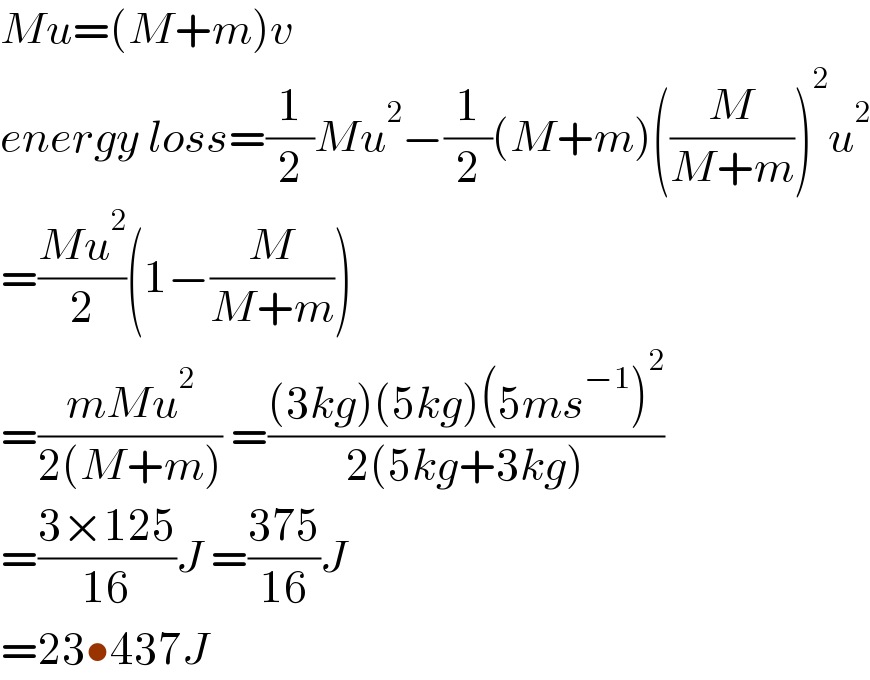
Mu=(M+m)v energy loss=(1/2)Mu^2 −(1/2)(M+m)((M/(M+m)))^2 u^2 =((Mu^2 )/2)(1−(M/(M+m))) =((mMu^2 )/(2(M+m))) =(((3kg)(5kg)(5ms^(−1) )^2 )/(2(5kg+3kg))) =((3×125)/(16))J =((375)/(16))J =23•437J
$${Mu}=\left({M}+{m}\right){v} \\ $$$${energy}\:{loss}=\frac{\mathrm{1}}{\mathrm{2}}{Mu}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left({M}+{m}\right)\left(\frac{{M}}{{M}+{m}}\right)^{\mathrm{2}} {u}^{\mathrm{2}} \\ $$$$=\frac{{Mu}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{1}−\frac{{M}}{{M}+{m}}\right) \\ $$$$=\frac{{mMu}^{\mathrm{2}} }{\mathrm{2}\left({M}+{m}\right)}\:=\frac{\left(\mathrm{3}{kg}\right)\left(\mathrm{5}{kg}\right)\left(\mathrm{5}{ms}^{−\mathrm{1}} \right)^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{5}{kg}+\mathrm{3}{kg}\right)} \\ $$$$=\frac{\mathrm{3}×\mathrm{125}}{\mathrm{16}}{J}\:=\frac{\mathrm{375}}{\mathrm{16}}{J} \\ $$$$=\mathrm{23}\bullet\mathrm{437}{J} \\ $$
Commented by Don08q last updated on 23/Jan/21
Thank you Sir
$${Thank}\:{you}\:{Sir} \\ $$
Answered by mr W last updated on 22/Jan/21
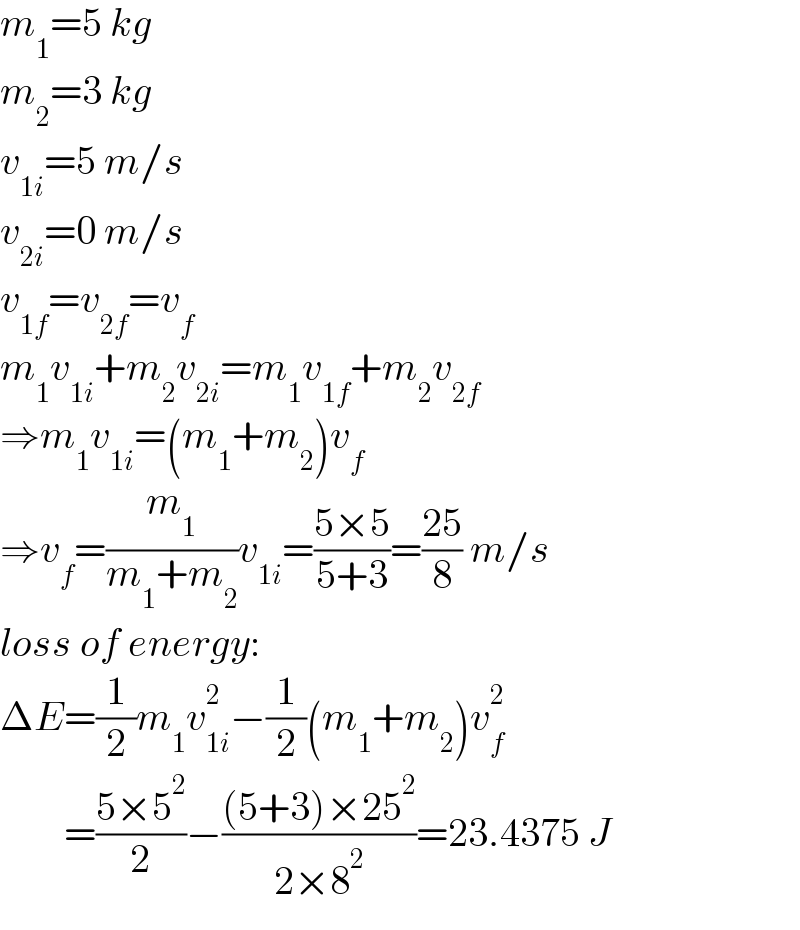
m_1 =5 kg m_2 =3 kg v_(1i) =5 m/s v_(2i) =0 m/s v_(1f) =v_(2f) =v_f m_1 v_(1i) +m_2 v_(2i) =m_1 v_(1f) +m_2 v_(2f) ⇒m_1 v_(1i) =(m_1 +m_2 )v_f ⇒v_f =(m_1 /(m_1 +m_2 ))v_(1i) =((5×5)/(5+3))=((25)/8) m/s loss of energy: ΔE=(1/2)m_1 v_(1i) ^2 −(1/2)(m_1 +m_2 )v_f ^2 =((5×5^2 )/2)−(((5+3)×25^2 )/(2×8^2 ))=23.4375 J
$${m}_{\mathrm{1}} =\mathrm{5}\:{kg} \\ $$$${m}_{\mathrm{2}} =\mathrm{3}\:{kg} \\ $$$${v}_{\mathrm{1}{i}} =\mathrm{5}\:{m}/{s} \\ $$$${v}_{\mathrm{2}{i}} =\mathrm{0}\:{m}/{s} \\ $$$${v}_{\mathrm{1}{f}} ={v}_{\mathrm{2}{f}} ={v}_{{f}} \\ $$$${m}_{\mathrm{1}} {v}_{\mathrm{1}{i}} +{m}_{\mathrm{2}} {v}_{\mathrm{2}{i}} ={m}_{\mathrm{1}} {v}_{\mathrm{1}{f}} +{m}_{\mathrm{2}} {v}_{\mathrm{2}{f}} \\ $$$$\Rightarrow{m}_{\mathrm{1}} {v}_{\mathrm{1}{i}} =\left({m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right){v}_{{f}} \\ $$$$\Rightarrow{v}_{{f}} =\frac{{m}_{\mathrm{1}} }{{m}_{\mathrm{1}} +{m}_{\mathrm{2}} }{v}_{\mathrm{1}{i}} =\frac{\mathrm{5}×\mathrm{5}}{\mathrm{5}+\mathrm{3}}=\frac{\mathrm{25}}{\mathrm{8}}\:{m}/{s} \\ $$$${loss}\:{of}\:{energy}: \\ $$$$\Delta{E}=\frac{\mathrm{1}}{\mathrm{2}}{m}_{\mathrm{1}} {v}_{\mathrm{1}{i}} ^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\left({m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right){v}_{{f}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{5}×\mathrm{5}^{\mathrm{2}} }{\mathrm{2}}−\frac{\left(\mathrm{5}+\mathrm{3}\right)×\mathrm{25}^{\mathrm{2}} }{\mathrm{2}×\mathrm{8}^{\mathrm{2}} }=\mathrm{23}.\mathrm{4375}\:{J} \\ $$
Commented by Don08q last updated on 22/Jan/21
Thank you Sir
$${Thank}\:{you}\:{Sir} \\ $$
Answered by Don08q last updated on 22/Jan/21
someone sent me this solution KE = (p^2 /(2m)) since momentum is conserved, m_1 u_1 = (m_1 +m_2 )v = p ⇒ p = 5kg×5ms^(−1) = 25kgms^(−1) KE_i = (p^2 /(2m_1 )) KE_f = (p^2 /(2(m_1 +m_2 )_ )) Energy loss = KE_i − KE_f = (p^2 /2)((1/m_1 ) − (1/(m_1 +m_2 ))) = (((25)^2 )/2)((1/5) − (1/(5+3))) = 23.4375 J
$$\mathrm{someone}\:\mathrm{sent}\:\mathrm{me}\:\mathrm{this}\:\mathrm{solution} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{KE}\:\:=\:\:\frac{{p}^{\mathrm{2}} }{\mathrm{2}{m}} \\ $$$$\mathrm{since}\:\mathrm{momentum}\:\mathrm{is}\:\mathrm{conserved}, \\ $$$$\:{m}_{\mathrm{1}} {u}_{\mathrm{1}} \:=\:\left({m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right){v}\:=\:{p} \\ $$$$\Rightarrow\:{p}\:=\:\mathrm{5}{kg}×\mathrm{5}{ms}^{−\mathrm{1}} \:=\:\mathrm{25}{kgms}^{−\mathrm{1}} \\ $$$${KE}_{{i}} \:=\:\frac{{p}^{\mathrm{2}} }{\mathrm{2}{m}_{\mathrm{1}} }\:\: \\ $$$${KE}_{{f}} \:=\:\frac{{p}^{\mathrm{2}} }{\mathrm{2}\left({m}_{\mathrm{1}} +{m}_{\mathrm{2}} \underset{} {\right)}} \\ $$$$\mathrm{Energy}\:\mathrm{loss}\:=\:{KE}_{{i}} \:−\:{KE}_{{f}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{{p}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{1}}{{m}_{\mathrm{1}} }\:−\:\frac{\mathrm{1}}{{m}_{\mathrm{1}} +{m}_{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\left(\mathrm{25}\right)^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{5}}\:−\:\frac{\mathrm{1}}{\mathrm{5}+\mathrm{3}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\mathrm{23}.\mathrm{4375}\:{J} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *