Question Number 110451 by mathmax by abdo last updated on 29/Aug/20
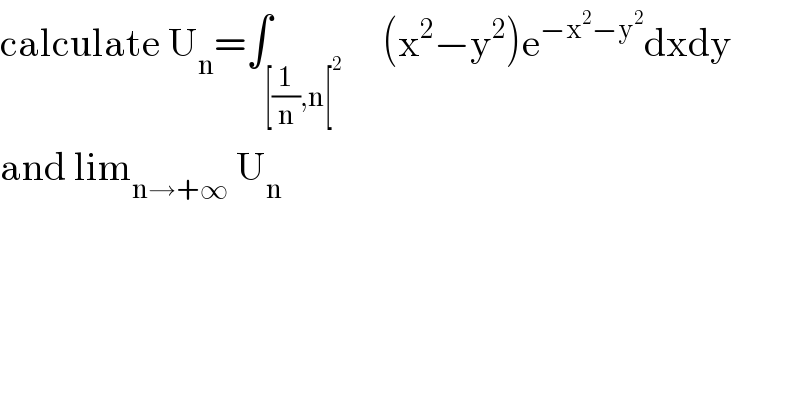
$$\mathrm{calculate}\:\mathrm{U}_{\mathrm{n}} =\int_{\left[\frac{\mathrm{1}}{\mathrm{n}},\mathrm{n}\left[^{\mathrm{2}} \right.\right.} \:\:\:\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} \right)\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} } \mathrm{dxdy} \\ $$$$\mathrm{and}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{U}_{\mathrm{n}} \\ $$
Answered by mathmax by abdo last updated on 31/Aug/20
![we consider the diffeomorphism { ((x =rcosθ)),((y =rsinθ)) :} 0≤x<n and 0≤y<n ⇒0≤x^2 +y^2 <2n^2 ⇒0≤r^2 <2n^2 ⇒0≤r<n(√2) ⇒U_n =∫∫_(0≤r<n(√2) and 0≤θ≤(π/2)) r^2 (cos^2 θ−sin^2 θ)e^(−r^2 ) rdrdθ =∫_0 ^(n(√2)) r^3 e^(−r^2 ) dr .∫_0 ^(π/2) cos(2θ)dθ but ∫_0 ^(π/2) cos(2θ)dθ =[(1/2)sin(2θ)]_0 ^(π/2) =0 ⇒ U_n =0 ∀n ⇒lim U_n =0](https://www.tinkutara.com/question/Q110840.png)
$$\mathrm{we}\:\mathrm{consider}\:\mathrm{the}\:\mathrm{diffeomorphism}\:\:\begin{cases}{\mathrm{x}\:=\mathrm{rcos}\theta}\\{\mathrm{y}\:=\mathrm{rsin}\theta}\end{cases} \\ $$$$\mathrm{0}\leqslant\mathrm{x}<\mathrm{n}\:\mathrm{and}\:\mathrm{0}\leqslant\mathrm{y}<\mathrm{n}\:\Rightarrow\mathrm{0}\leqslant\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} <\mathrm{2n}^{\mathrm{2}} \:\Rightarrow\mathrm{0}\leqslant\mathrm{r}^{\mathrm{2}} <\mathrm{2n}^{\mathrm{2}} \:\Rightarrow\mathrm{0}\leqslant\mathrm{r}<\mathrm{n}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{U}_{\mathrm{n}} =\int\int_{\mathrm{0}\leqslant\mathrm{r}<\mathrm{n}\sqrt{\mathrm{2}}\:\mathrm{and}\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}} \:\:\mathrm{r}^{\mathrm{2}} \left(\mathrm{cos}^{\mathrm{2}} \theta−\mathrm{sin}^{\mathrm{2}} \theta\right)\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \:\mathrm{rdrd}\theta \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{n}\sqrt{\mathrm{2}}} \:\:\:\mathrm{r}^{\mathrm{3}} \:\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \:\mathrm{dr}\:.\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\mathrm{cos}\left(\mathrm{2}\theta\right)\mathrm{d}\theta\:\:\:\mathrm{but}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}\left(\mathrm{2}\theta\right)\mathrm{d}\theta\:=\left[\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\mathrm{0}\:\Rightarrow\:\mathrm{U}_{\mathrm{n}} =\mathrm{0}\:\:\forall\mathrm{n}\:\Rightarrow\mathrm{lim}\:\mathrm{U}_{\mathrm{n}} =\mathrm{0} \\ $$
