Question Number 35035 by abdo mathsup 649 cc last updated on 14/May/18
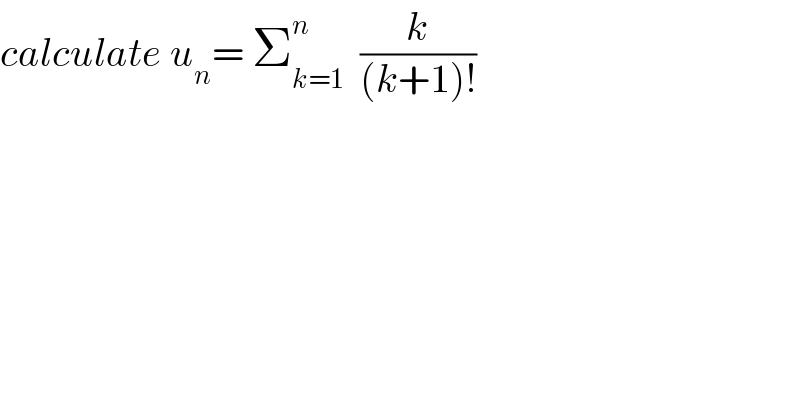
$${calculate}\:{u}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{{k}}{\left({k}+\mathrm{1}\right)!} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 14/May/18
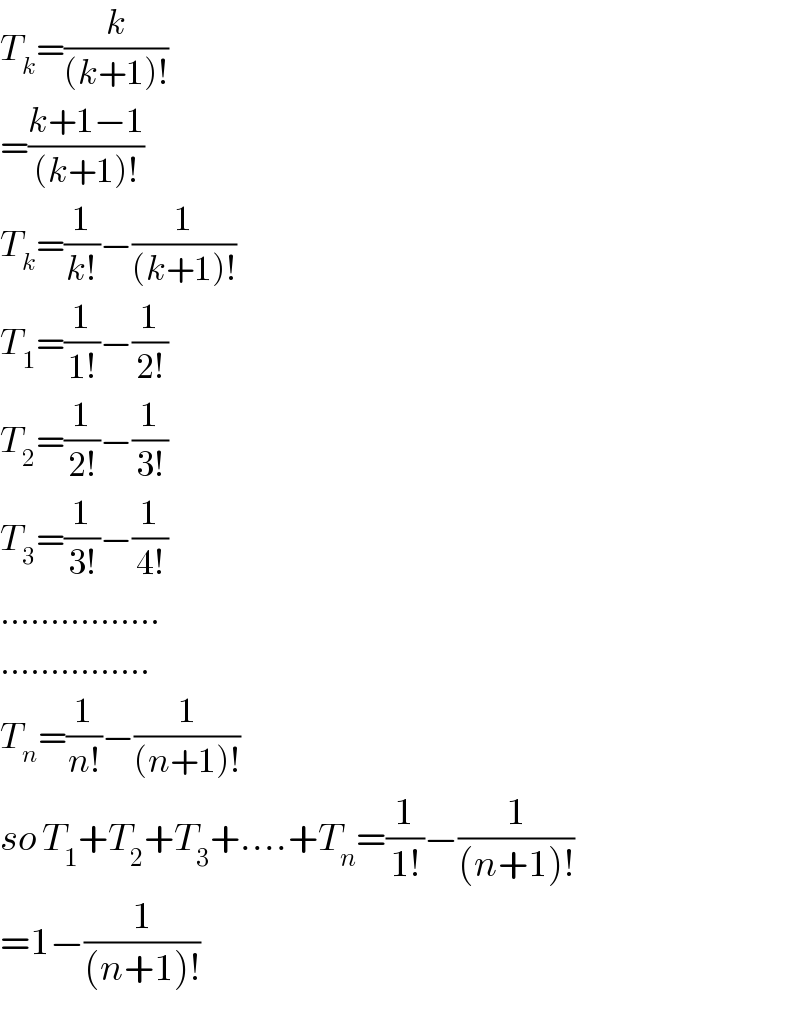
$${T}_{{k}} =\frac{{k}}{\left({k}+\mathrm{1}\right)!} \\ $$$$=\frac{{k}+\mathrm{1}−\mathrm{1}}{\left({k}+\mathrm{1}\right)!} \\ $$$${T}_{{k}} =\frac{\mathrm{1}}{{k}!}−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)!} \\ $$$${T}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}!}−\frac{\mathrm{1}}{\mathrm{2}!} \\ $$$${T}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!} \\ $$$${T}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{4}!} \\ $$$$……………. \\ $$$$…………… \\ $$$${T}_{{n}} =\frac{\mathrm{1}}{{n}!}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$${so}\:{T}_{\mathrm{1}} +{T}_{\mathrm{2}} +{T}_{\mathrm{3}} +….+{T}_{{n}} =\frac{\mathrm{1}}{\mathrm{1}!}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$
