Question Number 61258 by cesar.marval.larez@gmail.com last updated on 31/May/19
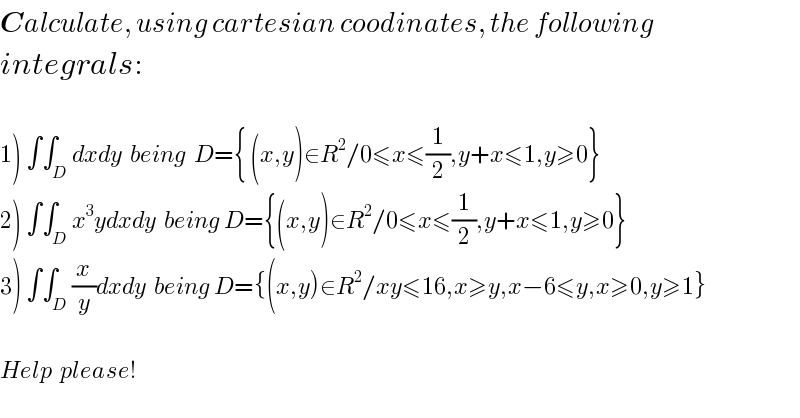
$$\boldsymbol{{C}}{alculate},\:{using}\:{cartesian}\:{coodinates},\:{the}\:{following} \\ $$$${integrals}: \\ $$$$ \\ $$$$\left.\mathrm{1}\right)\:\int\int_{{D}} {dxdy}\:\:{being}\:\:{D}=\left\{\:\left({x},{y}\right)\in{R}^{\mathrm{2}} /\mathrm{0}\leqslant{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}},{y}+{x}\leqslant\mathrm{1},{y}\geqslant\mathrm{0}\right\} \\ $$$$\left.\mathrm{2}\right)\:\int\int_{{D}} {x}^{\mathrm{3}} {ydxdy}\:\:{being}\:{D}=\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} /\mathrm{0}\leqslant{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}},{y}+{x}\leqslant\mathrm{1},{y}\geqslant\mathrm{0}\right\} \\ $$$$\left.\mathrm{3}\right)\:\int\int_{{D}} \frac{{x}}{{y}}{dxdy}\:\:{being}\:{D}=\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} /{xy}\leqslant\mathrm{16},{x}\geqslant{y},{x}−\mathrm{6}\leqslant{y},{x}\geqslant\mathrm{0},{y}\geqslant\mathrm{1}\right\} \\ $$$$ \\ $$$${Help}\:\:{please}! \\ $$
Commented by abdo mathsup 649 cc last updated on 31/May/19
![1) ∫∫ dxdy =∫_0 ^(1/2) (∫_0 ^(1−x) dy)dx =∫_0 ^(1/2) (1−x)dx =[x−(x^2 /2)]_0 ^(1/2) =(1/2) −(1/8) =((4−1)/8) =(3/8) .](https://www.tinkutara.com/question/Q61259.png)
$$\left.\mathrm{1}\right)\:\int\int\:{dxdy}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\left(\int_{\mathrm{0}} ^{\mathrm{1}−{x}} {dy}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{x}\right){dx}\:=\left[{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{8}}\:=\frac{\mathrm{4}−\mathrm{1}}{\mathrm{8}}\:=\frac{\mathrm{3}}{\mathrm{8}}\:. \\ $$
Commented by abdo mathsup 649 cc last updated on 31/May/19
![2) ∫∫ x^3 y dxdy =∫_0 ^(1/2) (∫_0 ^(1−x) ydy)x^3 dx =∫_0 ^(1/2) ([(y^2 /2)]_0 ^(1−x) )x^3 dx =(1/2) ∫_0 ^(1/2) (x−1)^2 x^3 dx =(1/2) ∫_0 ^(1/2) (x^2 −2x+1)x^3 dx =(1/2) ∫_0 ^(1/2) (x^5 −2x^4 +x^3 )dx =(1/2)[(x^6 /6) −(2/5) x^5 +(x^4 /4)]_0 ^(1/2) =(1/2){ (1/(6.2^6 )) −(2/(5.2^5 )) +(1/2^4 )} =....](https://www.tinkutara.com/question/Q61260.png)
$$\left.\mathrm{2}\right)\:\int\int\:{x}^{\mathrm{3}} {y}\:{dxdy}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\left(\int_{\mathrm{0}} ^{\mathrm{1}−{x}} {ydy}\right){x}^{\mathrm{3}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\left(\left[\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}−{x}} \right){x}^{\mathrm{3}} {dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} {x}^{\mathrm{3}} \:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}\right){x}^{\mathrm{3}} \:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\left({x}^{\mathrm{5}} −\mathrm{2}{x}^{\mathrm{4}} \:+{x}^{\mathrm{3}} \right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{x}^{\mathrm{6}} }{\mathrm{6}}\:−\frac{\mathrm{2}}{\mathrm{5}}\:{x}^{\mathrm{5}} \:+\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\mathrm{1}}{\mathrm{6}.\mathrm{2}^{\mathrm{6}} }\:−\frac{\mathrm{2}}{\mathrm{5}.\mathrm{2}^{\mathrm{5}} }\:+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }\right\}\:=…. \\ $$
Answered by perlman last updated on 31/May/19
![3)D=[(x,y).xy<16,x>y.x−6<y.x>0.y>1] =D_1 [(x,y). 1<y<x.1<x<4]∪D_2 [(x.y) 1<y<((16)/x).4<x<3+(√((30)))] ∫∫_(D1∪D2) f(x,y)dxdy=∫∫_(D1) f(x,y)dxdy+∫∫_(D2) f(x,y)dxdy if D1∩D2=∅ mor generaly is= if ∫∫_(D1∩D2) f(x,y)dxdy=0 “theorie of integration” So we integrate over D1 +integration over D_2 over D_1 =∫_1 ^4 (∫_1 ^x (x/y)dy)dx=∫_1 ^4 [xln(y)]_1 ^x dx=∫_1 ^4 (xln(x))dx =[(x^2 /2)ln(x)]_1 ^4 −∫_1 ^4 (x/2)dx=2ln(4)−[(x^2 /4)]_1 ^4 =2ln(4)−4+(1/4)=2ln(4)−((15)/4) ∫_4 ^(3+(√((30)))) ∫_1 ^((16)/x) (x/y)dydx=∫_4 ^(3+(√((30)))) xln(((16)/x))dx=∫_4 ^(3+(√((30)))) xln(16)dx−∫_4 ^(3+(√((30)))) xln(x)dx =[x^2 ln(16)]_4 ^(3+(√(30))) −[(x^2 /2)ln(x)−(x^2 /4)]_4 ^(3+(√(30)))](https://www.tinkutara.com/question/Q61286.png)
$$\left.\mathrm{3}\right){D}=\left[\left({x},{y}\right).{xy}<\mathrm{16},{x}>{y}.{x}−\mathrm{6}<{y}.{x}>\mathrm{0}.{y}>\mathrm{1}\right] \\ $$$$={D}_{\mathrm{1}} \left[\left({x},{y}\right).\:\mathrm{1}<{y}<{x}.\mathrm{1}<{x}<\mathrm{4}\right]\cup{D}_{\mathrm{2}} \left[\left({x}.{y}\right)\:\mathrm{1}<{y}<\frac{\mathrm{16}}{{x}}.\mathrm{4}<{x}<\mathrm{3}+\sqrt{\left(\mathrm{30}\right)}\right] \\ $$$$\int\int_{{D}\mathrm{1}\cup{D}\mathrm{2}} {f}\left({x},{y}\right){dxdy}=\int\int_{{D}\mathrm{1}} {f}\left({x},{y}\right){dxdy}+\int\int_{{D}\mathrm{2}} {f}\left({x},{y}\right){dxdy}\:{if}\:{D}\mathrm{1}\cap{D}\mathrm{2}=\varnothing \\ $$$${mor}\:{generaly}\:{is}=\:{if}\:\:\int\int_{{D}\mathrm{1}\cap{D}\mathrm{2}} {f}\left({x},{y}\right){dxdy}=\mathrm{0}\:“{theorie}\:{of}\:{integration}'' \\ $$$${So}\:{we}\:{integrate}\:{over}\:{D}\mathrm{1}\:+{integration}\:{over}\:{D}_{\mathrm{2}} \\ $$$${over}\:{D}_{\mathrm{1}} =\int_{\mathrm{1}} ^{\mathrm{4}} \left(\int_{\mathrm{1}} ^{{x}} \frac{{x}}{{y}}{dy}\right){dx}=\int_{\mathrm{1}} ^{\mathrm{4}} \left[{xln}\left({y}\right)\right]_{\mathrm{1}} ^{{x}} {dx}=\int_{\mathrm{1}} ^{\mathrm{4}} \left({xln}\left({x}\right)\right){dx} \\ $$$$=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{ln}\left({x}\right)\right]_{\mathrm{1}} ^{\mathrm{4}} −\int_{\mathrm{1}} ^{\mathrm{4}} \frac{{x}}{\mathrm{2}}{dx}=\mathrm{2}{ln}\left(\mathrm{4}\right)−\left[\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\right]_{\mathrm{1}} ^{\mathrm{4}} =\mathrm{2}{ln}\left(\mathrm{4}\right)−\mathrm{4}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{2}{ln}\left(\mathrm{4}\right)−\frac{\mathrm{15}}{\mathrm{4}} \\ $$$$\int_{\mathrm{4}} ^{\mathrm{3}+\sqrt{\left(\mathrm{30}\right)}} \int_{\mathrm{1}} ^{\frac{\mathrm{16}}{{x}}} \frac{{x}}{{y}}{dydx}=\int_{\mathrm{4}} ^{\mathrm{3}+\sqrt{\left(\mathrm{30}\right)}} {xln}\left(\frac{\mathrm{16}}{{x}}\right){dx}=\int_{\mathrm{4}} ^{\mathrm{3}+\sqrt{\left(\mathrm{30}\right)}} {xln}\left(\mathrm{16}\right){dx}−\int_{\mathrm{4}} ^{\mathrm{3}+\sqrt{\left(\mathrm{30}\right)}} {xln}\left({x}\right){dx} \\ $$$$=\left[{x}^{\mathrm{2}} {ln}\left(\mathrm{16}\right)\right]_{\mathrm{4}} ^{\mathrm{3}+\sqrt{\mathrm{30}}} −\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{ln}\left({x}\right)−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\right]_{\mathrm{4}} ^{\mathrm{3}+\sqrt{\mathrm{30}}} \\ $$
Commented by cesar.marval.larez@gmail.com last updated on 31/May/19

$${Haven}'{t}\:{graph}? \\ $$
