Question Number 60506 by prof Abdo imad last updated on 21/May/19
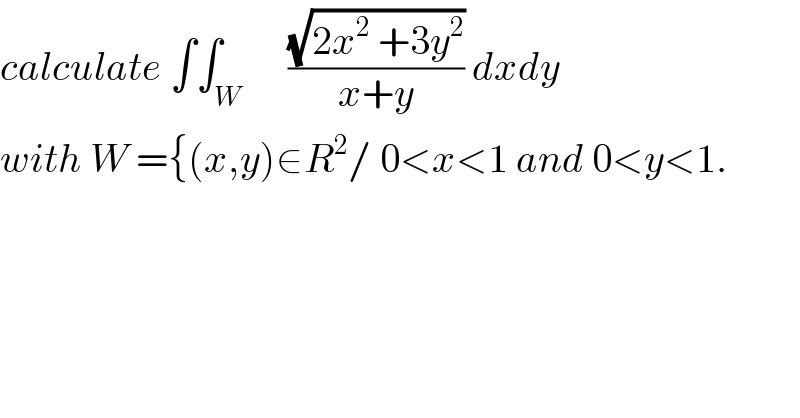
$${calculate}\:\int\int_{{W}} \:\:\:\:\:\frac{\sqrt{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}{y}^{\mathrm{2}} }}{{x}+{y}}\:{dxdy} \\ $$$${with}\:{W}\:=\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} /\:\mathrm{0}<{x}<\mathrm{1}\:{and}\:\mathrm{0}<{y}<\mathrm{1}.\right. \\ $$
Commented by Mr X pcx last updated on 23/May/19
![let consider the diffromorphism x=(r/( (√2))) cosθ and y =(r/( (√3))) sinθ 0<x^2 +y^2 <2 ⇒0<(r^2 /2) +(r^2 /3)<2 ⇒ 0<(5/6) r^2 <2 ⇒0<r^2 <((12)/5) ⇒0<r<((2(√3))/( (√5))) M_j = ((( (∂ϕ_1 /∂r) (∂ϕ_1 /∂θ))),(((∂ϕ_2 /∂r) (∂ϕ_2 /∂θ))) ) = ((((1/( (√2)))cosθ −(r/( (√2)))sinθ)),(((1/( (√3)))sinθ (r/( (√3)))cosθ)) ) det(M_j ) =(r/( (√2)(√3))) ⇒ I = ∫∫_(0<r<((2(√3))/( (√5))) and 0<θ<(π/2)) (r/((r/( (√2)))cosθ +(r/( (√3)))sinθ))(1/( (√6))) rdrdθ =∫_0 ^((2(√3))/( (√5))) rdr ∫_0 ^(π/2) (dθ/( (√3)cosθ +(√2)sinθ)) ∫_0 ^((2(√3))/( (√5))) rdr =[(r^2 /2)]_0 ^((2(√3))/( (√5))) =(1/2)(((4.3)/5)) =(6/5) ∫_0 ^(π/2) (dθ/( (√3)cosθ +(√2)sinθ)) =_(tan((θ/2)) =x) =∫_0 ^1 ((2dx)/((1+x^2 ){ (√3)((1−x^2 )/(1+x^2 )) +(√2) ((2x)/(1+x^2 ))})) =∫_0 ^1 ((2dx)/( (√3)−(√3)x^2 +2(√2)x)) =∫_0 ^1 ((−2dx)/( (√3)x^2 −2(√2)x −(√3))) let drcompose F(x)=((−2)/( (√3)x^2 −2(√2)x −(√3))) Δ^′ =2 +3 =5 ⇒x_1 =(((√2) +(√5))/( (√3))) x_2 =(((√2)−(√5))/( (√3))) ⇒ F(x) =((−2)/( (√3)(x−x_1 )(x−x_2 ))) =((−2)/( (√3)(x_1 −x_2 ))){ (1/(x−x_1 )) −(1/(x−x_2 ))} =((−2)/( (√3)(((2(√5))/( (√3)))))){ (1/(x−x_1 )) −(1/(x−x_2 ))} =−(1/( (√5))){ ....} ⇒ ∫_0 ^1 F(x)dx?=(1/( (√5)))[ln∣x−x_2 ∣−ln∣x−x_1 ∣] =(1/( (√5)))[ln∣((x−x_2 )/(x−x_1 ))∣]_0 ^1 =(1/( (√5)))( ln(((1−(((√2)−(√5))/( (√3))))/(1−(((√2) +(√5))/( (√3))))))−ln∣(((√2)−(√5))/( (√2) +(√5)))∣) =(1/( (√5)))( ln∣(((√3)−(√2)+(√5))/( (√3)−(√2) +(√5)))∣ −ln((((√5)−(√2))/( (√5) +(√2)))) so the vslue of I is known.](https://www.tinkutara.com/question/Q60657.png)
$${let}\:{consider}\:{the}\:{diffromorphism} \\ $$$${x}=\frac{{r}}{\:\sqrt{\mathrm{2}}}\:{cos}\theta\:\:{and}\:{y}\:=\frac{{r}}{\:\sqrt{\mathrm{3}}}\:{sin}\theta \\ $$$$\mathrm{0}<{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} <\mathrm{2}\:\Rightarrow\mathrm{0}<\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{{r}^{\mathrm{2}} }{\mathrm{3}}<\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{0}<\frac{\mathrm{5}}{\mathrm{6}}\:{r}^{\mathrm{2}} <\mathrm{2}\:\Rightarrow\mathrm{0}<{r}^{\mathrm{2}} <\frac{\mathrm{12}}{\mathrm{5}}\:\Rightarrow\mathrm{0}<{r}<\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{5}}} \\ $$$${M}_{{j}} =\begin{pmatrix}{\:\:\frac{\partial\varphi_{\mathrm{1}} }{\partial{r}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\partial\varphi_{\mathrm{1}} }{\partial\theta}}\\{\frac{\partial\varphi_{\mathrm{2}} }{\partial{r}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\partial\varphi_{\mathrm{2}} }{\partial\theta}}\end{pmatrix} \\ $$$$=\:\begin{pmatrix}{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{cos}\theta\:\:\:\:\:\:\:\:\:\:\:−\frac{{r}}{\:\sqrt{\mathrm{2}}}{sin}\theta}\\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{sin}\theta\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{r}}{\:\sqrt{\mathrm{3}}}{cos}\theta}\end{pmatrix} \\ $$$${det}\left({M}_{{j}} \right)\:=\frac{{r}}{\:\sqrt{\mathrm{2}}\sqrt{\mathrm{3}}}\:\:\:\Rightarrow \\ $$$${I}\:=\:\int\int_{\mathrm{0}<{r}<\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{5}}}\:\:\:{and}\:\:\mathrm{0}<\theta<\frac{\pi}{\mathrm{2}}} \:\:\frac{{r}}{\frac{{r}}{\:\sqrt{\mathrm{2}}}{cos}\theta\:+\frac{{r}}{\:\sqrt{\mathrm{3}}}{sin}\theta}\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:{rdrd}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{5}}}} \:\:{rdr}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{d}\theta}{\:\sqrt{\mathrm{3}}{cos}\theta\:+\sqrt{\mathrm{2}}{sin}\theta} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{5}}}} \:{rdr}\:=\left[\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{5}}}} \:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}.\mathrm{3}}{\mathrm{5}}\right)\:=\frac{\mathrm{6}}{\mathrm{5}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{d}\theta}{\:\sqrt{\mathrm{3}}{cos}\theta\:+\sqrt{\mathrm{2}}{sin}\theta}\:=_{{tan}\left(\frac{\theta}{\mathrm{2}}\right)\:={x}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left\{\:\sqrt{\mathrm{3}}\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:+\sqrt{\mathrm{2}}\:\frac{\mathrm{2}{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\right\}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{dx}}{\:\sqrt{\mathrm{3}}−\sqrt{\mathrm{3}}{x}^{\mathrm{2}} \:+\mathrm{2}\sqrt{\mathrm{2}}{x}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{−\mathrm{2}{dx}}{\:\sqrt{\mathrm{3}}{x}^{\mathrm{2}} \:−\mathrm{2}\sqrt{\mathrm{2}}{x}\:−\sqrt{\mathrm{3}}} \\ $$$${let}\:{drcompose}\:{F}\left({x}\right)=\frac{−\mathrm{2}}{\:\sqrt{\mathrm{3}}{x}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}{x}\:−\sqrt{\mathrm{3}}} \\ $$$$\Delta^{'} \:=\mathrm{2}\:+\mathrm{3}\:=\mathrm{5}\:\Rightarrow{x}_{\mathrm{1}} =\frac{\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{3}}} \\ $$$$\underset{\mathrm{2}} {{x}}=\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{−\mathrm{2}}{\:\sqrt{\mathrm{3}}\left({x}−{x}_{\mathrm{1}} \right)\left({x}−{x}_{\mathrm{2}} \right)} \\ $$$$=\frac{−\mathrm{2}}{\:\sqrt{\mathrm{3}}\left({x}_{\mathrm{1}} −{x}_{\mathrm{2}} \right)}\left\{\:\frac{\mathrm{1}}{{x}−{x}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{x}−{x}_{\mathrm{2}} }\right\} \\ $$$$=\frac{−\mathrm{2}}{\:\sqrt{\mathrm{3}}\left(\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{3}}}\right)}\left\{\:\frac{\mathrm{1}}{{x}−{x}_{\mathrm{1}} }\:−\frac{\mathrm{1}}{{x}−{x}_{\mathrm{2}} }\right\} \\ $$$$=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left\{\:….\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{F}\left({x}\right){dx}?=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left[{ln}\mid{x}−{x}_{\mathrm{2}} \mid−{ln}\mid{x}−{x}_{\mathrm{1}} \mid\right] \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left[{ln}\mid\frac{{x}−{x}_{\mathrm{2}} }{{x}−{x}_{\mathrm{1}} }\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\:{ln}\left(\frac{\mathrm{1}−\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}−\frac{\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{3}}}}\right)−{ln}\mid\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{5}}}\mid\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left(\:{ln}\mid\frac{\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{5}}}\mid\:−{ln}\left(\frac{\sqrt{\mathrm{5}}−\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{5}}\:+\sqrt{\mathrm{2}}}\right)\right. \\ $$$${so}\:{the}\:{vslue}\:{of}\:\:{I}\:{is}\:{known}. \\ $$
