calculate-w-x-y-e-x-y-dxdy-with-w-x-y-R-2-x-1-and-y-1-3-

Question Number 34292 by math khazana by abdo last updated on 03/May/18

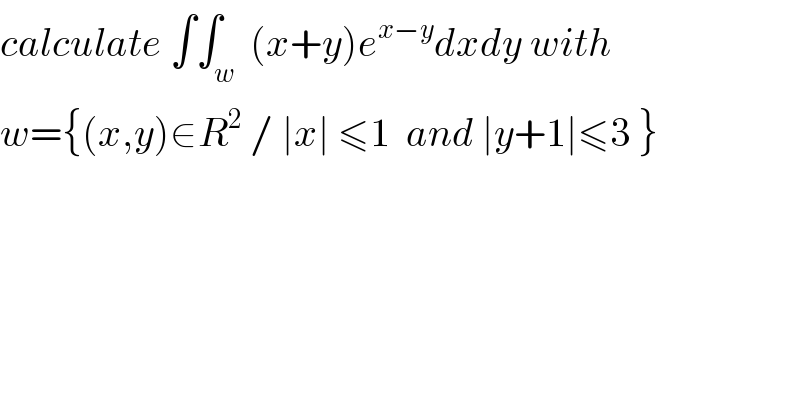
c a l c u l a t e \int \int_{w} (x + y) e^{x - y} d x d y w i t h

w = {(x, y) \in R^{2} / ∣ x ∣ ⩽ 1 a n d ∣ y + 1 ∣⩽ 3}

Commented by math khazana by abdo last updated on 07/May/18

∣ y + 1 ∣⩽ 3 \Leftrightarrow - 3 ⩽ y + 1 ⩽ 3 \Leftrightarrow - 4 ⩽ y ⩽ 4 s o

\int \int_{w} (x + y) e^{x - y} d x d y

= \int_{- 4}^{4} (\int_{- 1}^{1} (x + y) e^{x - y} d x) d y b u t

A (y) = \int_{- 1}^{1} (x + y) e^{x - y} d x = e^{- y} \int_{- 1}^{1} (x + y) e^{x} d x

= e^{- y} {{[(x + y) e^{x}]}_{- 1}^{1} - \int_{- 1}^{1} e^{x} d x}

= e^{- y} {(1 + y) e - (- 1 + y) e^{- 1} - (e - e^{- 1})}

= e (1 + y) e^{- y} + e^{- 1} (1 - y) e^{- y} - (e - e^{- 1}) e^{- y}

\int \int_{w} (x + y) e^{x - y} d x d y

= e \int_{- 4}^{4} (1 + y) e^{- y} d y + e^{- 1} \int_{- 4}^{4} (1 - y) e^{- y} - (e - e^{- 1}) \int_{- 4}^{4} e^{- y} d y

b y p a r t s

\int_{- 4}^{4} (1 + y) e^{- y} d y = {[- (1 + y) e^{- y}]}_{- 4}^{4} + \int_{- 4}^{4} e^{- y} d y

= - 3 e^{4} - 5 e^{- 4} + {[- e^{- y}]}_{- 4}^{4}

= - 3 e^{4} - 5 e^{- 4} + e^{4} - e^{- 4}

w e f o l l o w t h e ? s a m e m e t h o d f o r t h e o t h e r i n t e g r a l s

\dots