Question Number 34289 by math khazana by abdo last updated on 03/May/18
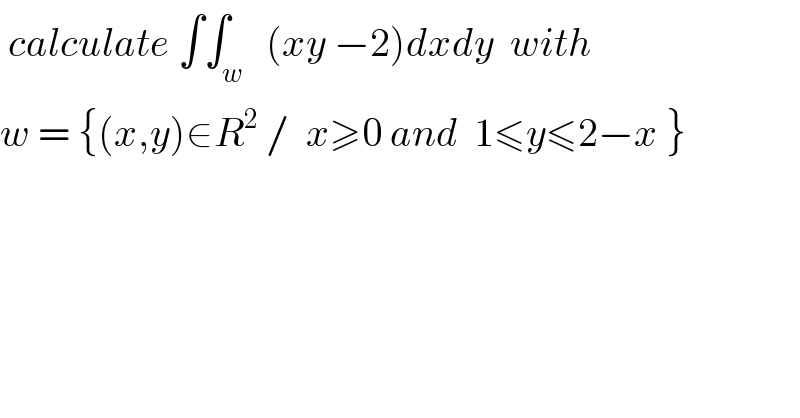
$$\:{calculate}\:\int\int_{{w}} \:\:\left({xy}\:−\mathrm{2}\right){dxdy}\:\:{with}\: \\ $$$${w}\:=\:\left\{\left({x},{y}\right)\in{R}^{\mathrm{2}} \:/\:\:{x}\geqslant\mathrm{0}\:{and}\:\:\mathrm{1}\leqslant{y}\leqslant\mathrm{2}−{x}\:\right\} \\ $$
Commented by math khazana by abdo last updated on 07/May/18
![1≤2−x ⇒ 2−x≥1 ⇒ 1≥x ⇒ 0≤x≤1 ⇒ ∫∫_w (xy−2)dxdy = ∫_0 ^1 (∫_1 ^(2−x) (xy−2)dy)dx but ∫_1 ^(2−x) (xy−2)dy = [x(y^2 /2) −2y]_(y=1) ^(y=2−x) =x(((2−x)^2 )/2) −2(2−x) −(x/2) +2 =(x/2)(x^2 −4x+4) −4 +2x −(x/2) +2 =(x^3 /2) −2x^2 +2x +2x −(x/2) −2 =(x^3 /2) −2x^2 +(7/2)x −2 ∫∫_w (xy−2)dxdy = ∫_0 ^1 ((x^3 /2) −2 x^2 +(7/2)x −2)dx =[ (1/8)x^4 −(2/3)x^3 +(7/4)x^2 −2x]_0 ^1 =(1/8) −(2/3) +(7/4) −2 =((−13)/(24)) −(1/4) = ((−19)/(24)) .](https://www.tinkutara.com/question/Q34483.png)
$$\mathrm{1}\leqslant\mathrm{2}−{x}\:\Rightarrow\:\mathrm{2}−{x}\geqslant\mathrm{1}\:\Rightarrow\:\mathrm{1}\geqslant{x}\:\Rightarrow\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:\Rightarrow \\ $$$$\int\int_{{w}} \left({xy}−\mathrm{2}\right){dxdy}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\int_{\mathrm{1}} ^{\mathrm{2}−{x}} \left({xy}−\mathrm{2}\right){dy}\right){dx}\:{but} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}−{x}} \:\left({xy}−\mathrm{2}\right){dy}\:=\:\left[{x}\frac{{y}^{\mathrm{2}} }{\mathrm{2}}\:−\mathrm{2}{y}\right]_{{y}=\mathrm{1}} ^{{y}=\mathrm{2}−{x}} \\ $$$$={x}\frac{\left(\mathrm{2}−{x}\right)^{\mathrm{2}} }{\mathrm{2}}\:−\mathrm{2}\left(\mathrm{2}−{x}\right)\:−\frac{{x}}{\mathrm{2}}\:+\mathrm{2} \\ $$$$=\frac{{x}}{\mathrm{2}}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right)\:−\mathrm{4}\:+\mathrm{2}{x}\:−\frac{{x}}{\mathrm{2}}\:+\mathrm{2} \\ $$$$=\frac{{x}^{\mathrm{3}} }{\mathrm{2}}\:−\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{2}{x}\:\:+\mathrm{2}{x}\:−\frac{{x}}{\mathrm{2}}\:−\mathrm{2} \\ $$$$=\frac{{x}^{\mathrm{3}} }{\mathrm{2}}\:\:−\mathrm{2}{x}^{\mathrm{2}} \:\:+\frac{\mathrm{7}}{\mathrm{2}}{x}\:−\mathrm{2} \\ $$$$\int\int_{{w}} \left({xy}−\mathrm{2}\right){dxdy}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{{x}^{\mathrm{3}} }{\mathrm{2}}\:−\mathrm{2}\:{x}^{\mathrm{2}} \:+\frac{\mathrm{7}}{\mathrm{2}}{x}\:−\mathrm{2}\right){dx} \\ $$$$=\left[\:\frac{\mathrm{1}}{\mathrm{8}}{x}^{\mathrm{4}} \:\:−\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} \:\:+\frac{\mathrm{7}}{\mathrm{4}}{x}^{\mathrm{2}} \:−\mathrm{2}{x}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\:−\frac{\mathrm{2}}{\mathrm{3}}\:+\frac{\mathrm{7}}{\mathrm{4}}\:−\mathrm{2} \\ $$$$=\frac{−\mathrm{13}}{\mathrm{24}}\:\:−\frac{\mathrm{1}}{\mathrm{4}}\:=\:\frac{−\mathrm{19}}{\mathrm{24}}\:. \\ $$
