Menu Close

calculate-x-2-cos-4x-x-2-1-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 39119 by math khazana by abdo last updated on 02/Jul/18
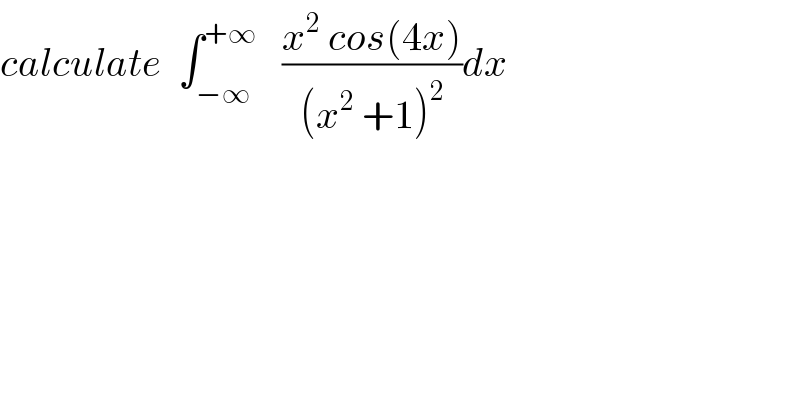
calculate ∫_(−∞) ^(+∞) ((x^2 cos(4x))/((x^2 +1)^2 ))dx
$${calculate}\:\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{x}^{\mathrm{2}} \:{cos}\left(\mathrm{4}{x}\right)}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Commented by math khazana by abdo last updated on 03/Jul/18
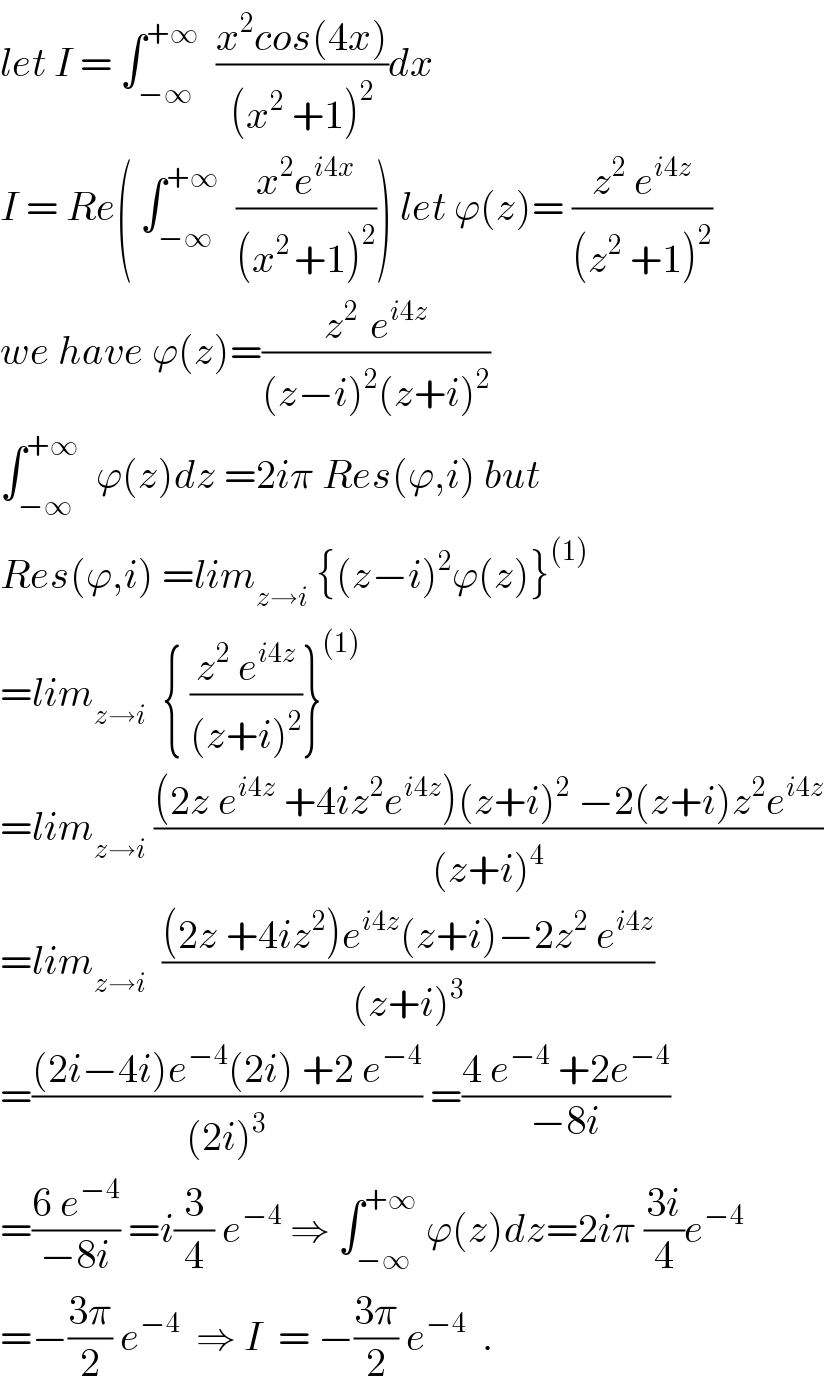
let I = ∫_(−∞) ^(+∞) ((x^2 cos(4x))/((x^2 +1)^2 ))dx I = Re( ∫_(−∞) ^(+∞) ((x^2 e^(i4x) )/((x^(2 ) +1)^2 ))) let ϕ(z)= ((z^2 e^(i4z) )/((z^2 +1)^2 )) we have ϕ(z)=((z^(2 ) e^(i4z) )/((z−i)^2 (z+i)^2 )) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,i) but Res(ϕ,i) =lim_(z→i) {(z−i)^2 ϕ(z)}^((1)) =lim_(z→i) { ((z^2 e^(i4z) )/((z+i)^2 ))}^((1)) =lim_(z→i) (((2z e^(i4z) +4iz^2 e^(i4z) )(z+i)^2 −2(z+i)z^2 e^(i4z) )/((z+i)^4 )) =lim_(z→i) (((2z +4iz^2 )e^(i4z) (z+i)−2z^2 e^(i4z) )/((z+i)^3 )) =(((2i−4i)e^(−4) (2i) +2 e^(−4) )/((2i)^3 )) =((4 e^(−4) +2e^(−4) )/(−8i)) =((6 e^(−4) )/(−8i)) =i(3/4) e^(−4) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz=2iπ ((3i)/4)e^(−4) =−((3π)/2) e^(−4) ⇒ I = −((3π)/2) e^(−4) .
$${let}\:{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} {cos}\left(\mathrm{4}{x}\right)}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$${I}\:=\:{Re}\left(\:\int_{−\infty} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} {e}^{{i}\mathrm{4}{x}} }{\left({x}^{\mathrm{2}\:} +\mathrm{1}\right)^{\mathrm{2}} }\right)\:{let}\:\varphi\left({z}\right)=\:\frac{{z}^{\mathrm{2}} \:{e}^{{i}\mathrm{4}{z}} }{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${we}\:{have}\:\varphi\left({z}\right)=\frac{{z}^{\mathrm{2}\:} \:{e}^{{i}\mathrm{4}{z}} }{\left({z}−{i}\right)^{\mathrm{2}} \left({z}+{i}\right)^{\mathrm{2}} } \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{i}\right)\:{but} \\ $$$${Res}\left(\varphi,{i}\right)\:={lim}_{{z}\rightarrow{i}} \:\left\{\left({z}−{i}\right)^{\mathrm{2}} \varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\left\{\:\frac{{z}^{\mathrm{2}} \:{e}^{{i}\mathrm{4}{z}} }{\left({z}+{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}} \:\frac{\left(\mathrm{2}{z}\:{e}^{{i}\mathrm{4}{z}} \:+\mathrm{4}{iz}^{\mathrm{2}} {e}^{{i}\mathrm{4}{z}} \right)\left({z}+{i}\right)^{\mathrm{2}} \:−\mathrm{2}\left({z}+{i}\right){z}^{\mathrm{2}} {e}^{{i}\mathrm{4}{z}} }{\left({z}+{i}\right)^{\mathrm{4}} } \\ $$$$={lim}_{{z}\rightarrow{i}} \:\:\frac{\left(\mathrm{2}{z}\:+\mathrm{4}{iz}^{\mathrm{2}} \right){e}^{{i}\mathrm{4}{z}} \left({z}+{i}\right)−\mathrm{2}{z}^{\mathrm{2}} \:{e}^{{i}\mathrm{4}{z}} }{\left({z}+{i}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left(\mathrm{2}{i}−\mathrm{4}{i}\right){e}^{−\mathrm{4}} \left(\mathrm{2}{i}\right)\:+\mathrm{2}\:{e}^{−\mathrm{4}} }{\left(\mathrm{2}{i}\right)^{\mathrm{3}} }\:=\frac{\mathrm{4}\:{e}^{−\mathrm{4}} \:+\mathrm{2}{e}^{−\mathrm{4}} }{−\mathrm{8}{i}} \\ $$$$=\frac{\mathrm{6}\:{e}^{−\mathrm{4}} }{−\mathrm{8}{i}}\:={i}\frac{\mathrm{3}}{\mathrm{4}}\:{e}^{−\mathrm{4}} \:\Rightarrow\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}=\mathrm{2}{i}\pi\:\frac{\mathrm{3}{i}}{\mathrm{4}}{e}^{−\mathrm{4}} \\ $$$$=−\frac{\mathrm{3}\pi}{\mathrm{2}}\:{e}^{−\mathrm{4}} \:\:\Rightarrow\:{I}\:\:=\:−\frac{\mathrm{3}\pi}{\mathrm{2}}\:{e}^{−\mathrm{4}} \:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *