Menu Close

calculate-x-2-dx-x-2-x-1-3-

Tinku Tara 0 Comments
Pin




Question Number 102165 by mathmax by abdo last updated on 07/Jul/20
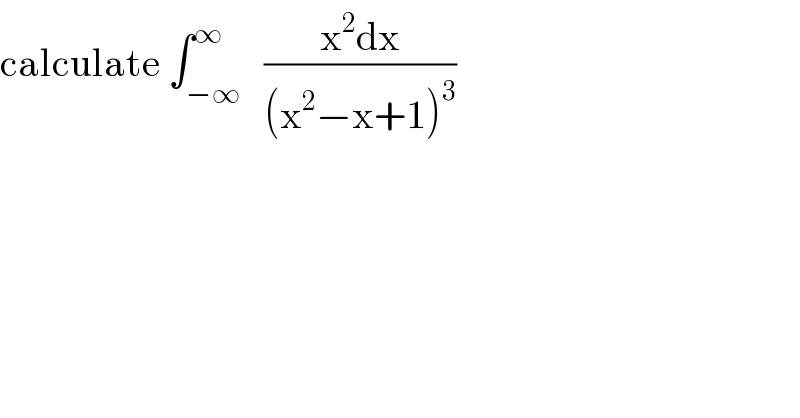
calculate ∫_(−∞) ^∞ ((x^2 dx)/((x^2 −x+1)^3 ))
$$\mathrm{calculate}\:\int_{−\infty} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$
Answered by MAB last updated on 07/Jul/20
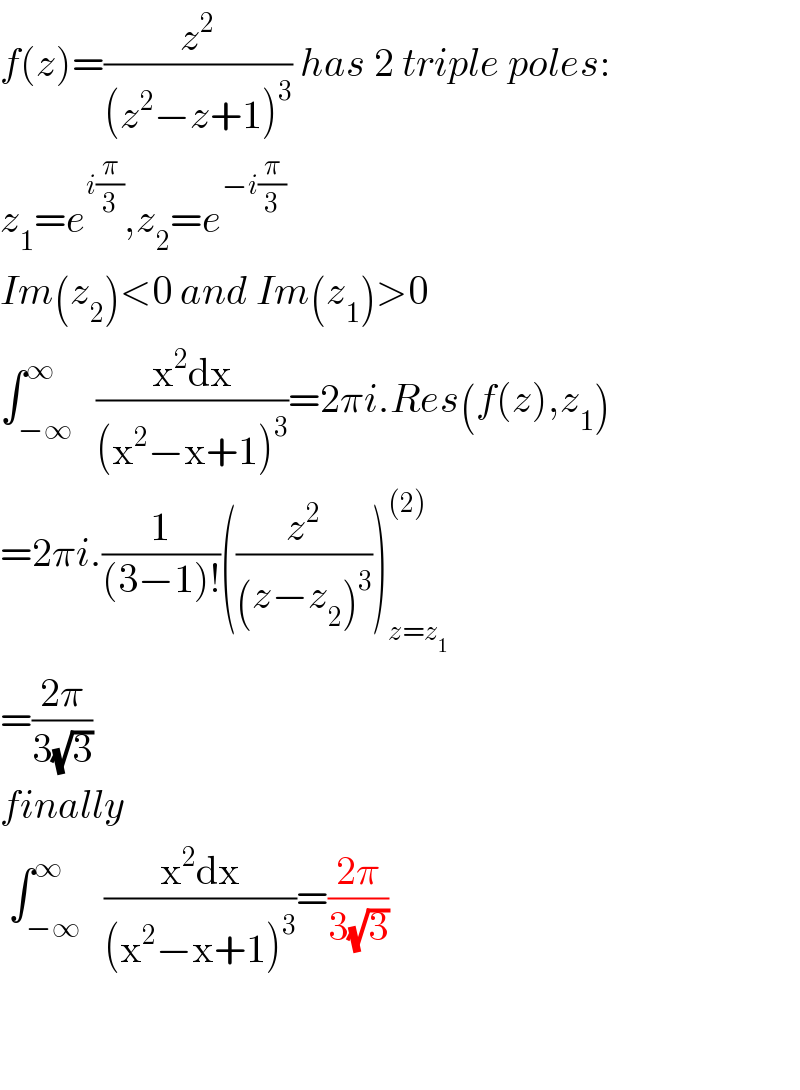
f(z)=(z^2 /((z^2 −z+1)^3 )) has 2 triple poles: z_1 =e^(i(π/3)) ,z_2 =e^(−i(π/3)) Im(z_2 )<0 and Im(z_1 )>0 ∫_(−∞) ^∞ ((x^2 dx)/((x^2 −x+1)^3 ))=2πi.Res(f(z),z_1 ) =2πi.(1/((3−1)!))((z^2 /((z−z_2 )^3 )))_(z=z_1 ) ^((2)) =((2π)/(3(√3))) finally ∫_(−∞) ^∞ ((x^2 dx)/((x^2 −x+1)^3 ))=((2π)/(3(√3)))
$${f}\left({z}\right)=\frac{{z}^{\mathrm{2}} }{\left({z}^{\mathrm{2}} −{z}+\mathrm{1}\right)^{\mathrm{3}} }\:{has}\:\mathrm{2}\:{triple}\:{poles}:\: \\ $$$${z}_{\mathrm{1}} ={e}^{{i}\frac{\pi}{\mathrm{3}}} ,{z}_{\mathrm{2}} ={e}^{−{i}\frac{\pi}{\mathrm{3}}} \\ $$$${Im}\left({z}_{\mathrm{2}} \right)<\mathrm{0}\:{and}\:{Im}\left({z}_{\mathrm{1}} \right)>\mathrm{0} \\ $$$$\int_{−\infty} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }=\mathrm{2}\pi{i}.{Res}\left({f}\left({z}\right),{z}_{\mathrm{1}} \right) \\ $$$$=\mathrm{2}\pi{i}.\frac{\mathrm{1}}{\left(\mathrm{3}−\mathrm{1}\right)!}\left(\frac{{z}^{\mathrm{2}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{3}} }\right)_{{z}={z}_{\mathrm{1}} } ^{\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$${finally} \\ $$$$\:\int_{−\infty} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 07/Jul/20
I =∫_(−∞) ^(+∞) ((x^2 dx)/((x^2 −x+1)^3 )) let ϕ(z) =(z^2 /((z^2 −z+1)^3 )) pole of ϕ z^2 −z+1 =0 →Δ =−3 ⇒z_1 =((1+i(√3))/2) =e^((iπ)/3) and z_2 =((1−i(√3))/2) =e^(−((iπ)/3)) ⇒ϕ(z) =(z^2 /((z−z_1 )^3 (z−z_2 )^3 )) the poles of ϕ are e^((iπ)/3) and e^(−((iπ)/3) ) (triples) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,e^((iπ)/3) ) and Res(ϕ,e^((iπ)/3) ) =lim_(z→e^((iπ)/3) ) (1/((3−1)!)){(z−e^((iπ)/3) )^3 ϕ(z)}^((2)) =(1/2)lim_(z→e^((iπ)/3) ) {(z^2 /((z−e^(−((iπ)/3)) )^3 ))}^((2)) =lim_(z→e^((iπ)/3) ) {((2z(z−e^(−((iπ)/3)) )^3 −3(z−e^(−((iπ)/3)) )^2 z^2 )/((z−e^(−((iπ)/3)) )^6 ))}^((1)) =lim_(z→e^((iπ)/3) ) { ((2z(z−e^(−((iπ)/3)) )−3z^2 )/((z−e^(−((iπ)/3)) )^4 ))}^((1)) =lim_(z→e^((iπ)/3) ) {((−z^2 −2z e^(−((iπ)/3)) )/((z−e^(−((iπ)/3)) )^4 ))}^((1)) −lim_(z→e^((iπ)/3) ) (((2z+2e^(−((iπ)/3)) )(z−e^(−((iπ)/3)) )^4 −4(z−e^(−((iπ)/3)) )^3 (z^2 +2z e^(−((iπ)/3)) ))/((z−e^(−((iπ)/3)) )^8 )) =−lim_(z→e^((iπ)/3) ) (((2z+2e^(−((iπ)/3)) )(z−e^(−((iπ)/3)) )−4(z^2 +2z e^(−((iπ)/3)) ))/((z−e^(−((iπ)/3)) )^5 )) =− ((4cos((π/3))2isin((π/3))−4{e^((2iπ)/3) +2})/((2isin((π/3)))^5 )) =−((8×(1/2)×((√3)/2)i−8 −4e^((i2π)/3) )/(32i(((√3)/2))^5 )) =((2(√3)i −8 −4(−(1/2)+((i(√3))/2)))/(32i(((√3)/2))^5 )) =(6/(32i((√3))^5 ))×(2^5 /( (√3))) =(6/(i((√3))^6 )) =(6/(3^3 i)) =(2/(9i)) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπ×(2/(9i)) =((4π)/9) ⇒ I =((4π)/9)
$$\mathrm{I}\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{3}} }\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\right)^{\mathrm{3}} }\:\:\mathrm{pole}\:\mathrm{of}\:\varphi \\ $$$$\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta\:=−\mathrm{3}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\Rightarrow\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)^{\mathrm{3}} \left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\varphi\:\mathrm{are}\:\:\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}\:} \left(\mathrm{triples}\right)\:\:\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:\mathrm{and}\: \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\frac{\mathrm{1}}{\left(\mathrm{3}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} \:\varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\:\:\left\{\frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} }\right\}^{\left(\mathrm{2}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\:\left\{\frac{\mathrm{2z}\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} \mathrm{z}^{\mathrm{2}} }{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{6}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:} \:\:\:\left\{\:\frac{\mathrm{2z}\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)−\mathrm{3z}^{\mathrm{2}} }{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\:\left\{\frac{−\mathrm{z}^{\mathrm{2}} −\mathrm{2z}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} }{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$−\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\:\frac{\left(\mathrm{2z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} \:−\mathrm{4}\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} \left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{2z}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)}{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{8}} } \\ $$$$=−\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} } \:\:\frac{\left(\mathrm{2z}+\mathrm{2e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)−\mathrm{4}\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{2z}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)}{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{5}} } \\ $$$$=−\:\:\:\frac{\mathrm{4cos}\left(\frac{\pi}{\mathrm{3}}\right)\mathrm{2isin}\left(\frac{\pi}{\mathrm{3}}\right)−\mathrm{4}\left\{\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \:+\mathrm{2}\right\}}{\left(\mathrm{2isin}\left(\frac{\pi}{\mathrm{3}}\right)\right)^{\mathrm{5}} } \\ $$$$=−\frac{\mathrm{8}×\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}−\mathrm{8}\:−\mathrm{4e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} }{\mathrm{32i}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{5}} }\:=\frac{\mathrm{2}\sqrt{\mathrm{3}}\mathrm{i}\:−\mathrm{8}\:−\mathrm{4}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}{\mathrm{32i}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{5}} } \\ $$$$=\frac{\mathrm{6}}{\mathrm{32i}\left(\sqrt{\mathrm{3}}\right)^{\mathrm{5}} }×\frac{\mathrm{2}^{\mathrm{5}} }{\:\sqrt{\mathrm{3}}}\:=\frac{\mathrm{6}}{\mathrm{i}\left(\sqrt{\mathrm{3}}\right)^{\mathrm{6}} }\:=\frac{\mathrm{6}}{\mathrm{3}^{\mathrm{3}} \mathrm{i}}\:=\frac{\mathrm{2}}{\mathrm{9i}}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi×\frac{\mathrm{2}}{\mathrm{9i}}\:=\frac{\mathrm{4}\pi}{\mathrm{9}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\frac{\mathrm{4}\pi}{\mathrm{9}} \\ $$
Commented by mathmax by abdo last updated on 07/Jul/20
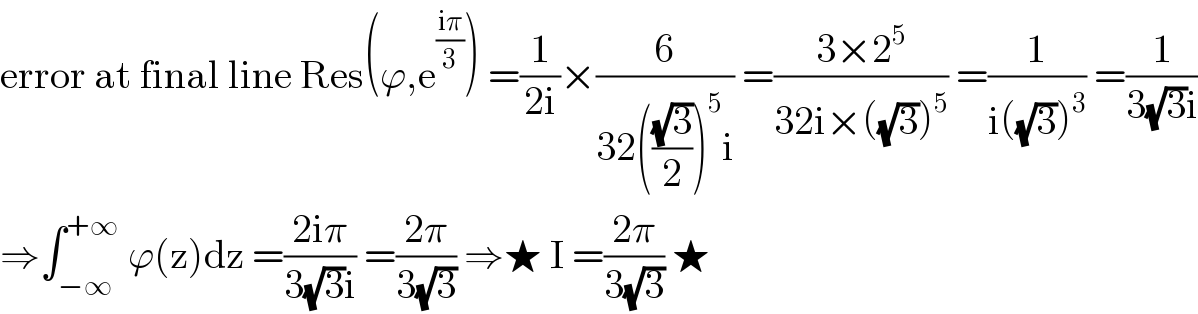
error at final line Res(ϕ,e^((iπ)/3) ) =(1/(2i))×(6/(32(((√3)/2))^5 i)) =((3×2^5 )/(32i×((√3))^5 )) =(1/(i((√3))^3 )) =(1/(3(√3)i)) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =((2iπ)/(3(√3)i)) =((2π)/(3(√3))) ⇒★ I =((2π)/(3(√3))) ★
$$\mathrm{error}\:\mathrm{at}\:\mathrm{final}\:\mathrm{line}\:\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:=\frac{\mathrm{1}}{\mathrm{2i}}×\frac{\mathrm{6}}{\mathrm{32}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{5}} \mathrm{i}}\:=\frac{\mathrm{3}×\mathrm{2}^{\mathrm{5}} }{\mathrm{32i}×\left(\sqrt{\mathrm{3}}\right)^{\mathrm{5}} }\:=\frac{\mathrm{1}}{\mathrm{i}\left(\sqrt{\mathrm{3}}\right)^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}} \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\frac{\mathrm{2i}\pi}{\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}}\:=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\Rightarrow\bigstar\:\mathrm{I}\:=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\bigstar \\ $$
Commented by MAB last updated on 07/Jul/20
exact sir
$${exact}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *