Menu Close

calculate-x-2-x-2-x-1-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 117253 by mathmax by abdo last updated on 10/Oct/20
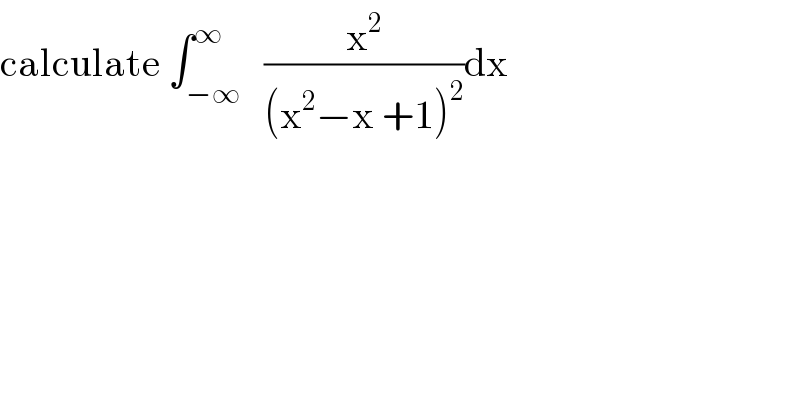
calculate ∫_(−∞) ^∞ (x^2 /((x^2 −x +1)^2 ))dx
$$\mathrm{calculate}\:\int_{−\infty} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Answered by mnjuly1970 last updated on 10/Oct/20
=∫_(−∞) ^( +∞) ((x^2 −x+1+x−1)/((x^2 −x+1)^2 ))dx =∫_(−∞) ^( +∞) (1/(x^2 −x+1))dx +(1/2)∫_(−∞) ^( +∞) ((2x−1−1)/((x^2 −x+1)^2 ))dx ({∫_(−∞) ^( +∞) (1/((x−(1/2))^2 +(((√3)/2))^2 ))dx}=k_1 ) −([(1/(2(x^2 −x+1)))]_(−∞) ^( ∞) =k_2 )−(1/2){∫_(−∞) ^( +∞) (1/((x^2 −x+1)^2 ))dx}=k_3 k_1 =((2π)/( (√3))) , k_2 =0 k_3 =∫_(−∞) ^( +∞) (1/((x^2 −x+1)^2 ))dx Λ(b)=∫_(−∞) ^( +∞) (1/(x^2 −x+b))dx=∫_(−∞) ^( +∞) (1/((x−(1/2))^2 +(((√(4b−1))/2))^2 )) =((2π)/( (√(4b−1)))) k_3 =−Λ^′ (b)∣_(b=1) =−2π(((−1)/2))(4)(4b−1)^(−(3/2)) ∣_(b=1) =(4π)(1/( 3(√3))) ∴ ∫_(−∞) ^( +∞) (x^2 /((x^2 −x+1)^2 ))dx=((2π)/( (√3)))−((2π)/(3(√3)))=((4π)/( 3(√3))) ....m.n.july.1970...
$$=\int_{−\infty} ^{\:+\infty} \frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}+{x}−\mathrm{1}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{−\infty} ^{\:+\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\:+\infty} \frac{\mathrm{2}{x}−\mathrm{1}−\mathrm{1}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\left(\left\{\int_{−\infty} ^{\:+\infty} \frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}\right\}={k}_{\mathrm{1}} \right)\:−\left(\left[\frac{\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}\right]_{−\infty} ^{\:\infty} ={k}_{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{2}}\left\{\int_{−\infty} ^{\:+\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\right\}={k}_{\mathrm{3}} \\ $$$${k}_{\mathrm{1}} =\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}\:,\:{k}_{\mathrm{2}} =\mathrm{0} \\ $$$${k}_{\mathrm{3}} =\int_{−\infty} ^{\:+\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\:\Lambda\left({b}\right)=\int_{−\infty} ^{\:+\infty} \frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}+{b}}{dx}=\int_{−\infty} ^{\:+\infty} \frac{\mathrm{1}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{4}{b}−\mathrm{1}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{4}{b}−\mathrm{1}}}\: \\ $$$${k}_{\mathrm{3}} =−\Lambda^{'} \left({b}\right)\mid_{{b}=\mathrm{1}} =−\mathrm{2}\pi\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{4}\right)\left(\mathrm{4}{b}−\mathrm{1}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \mid_{{b}=\mathrm{1}} =\left(\mathrm{4}\pi\right)\frac{\mathrm{1}}{\:\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\therefore\:\int_{−\infty} ^{\:+\infty} \frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}}−\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}=\frac{\mathrm{4}\pi}{\:\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:….{m}.{n}.{july}.\mathrm{1970}… \\ $$$$\:\:\:\: \\ $$$$ \\ $$$$\:\: \\ $$
Answered by Bird last updated on 10/Oct/20
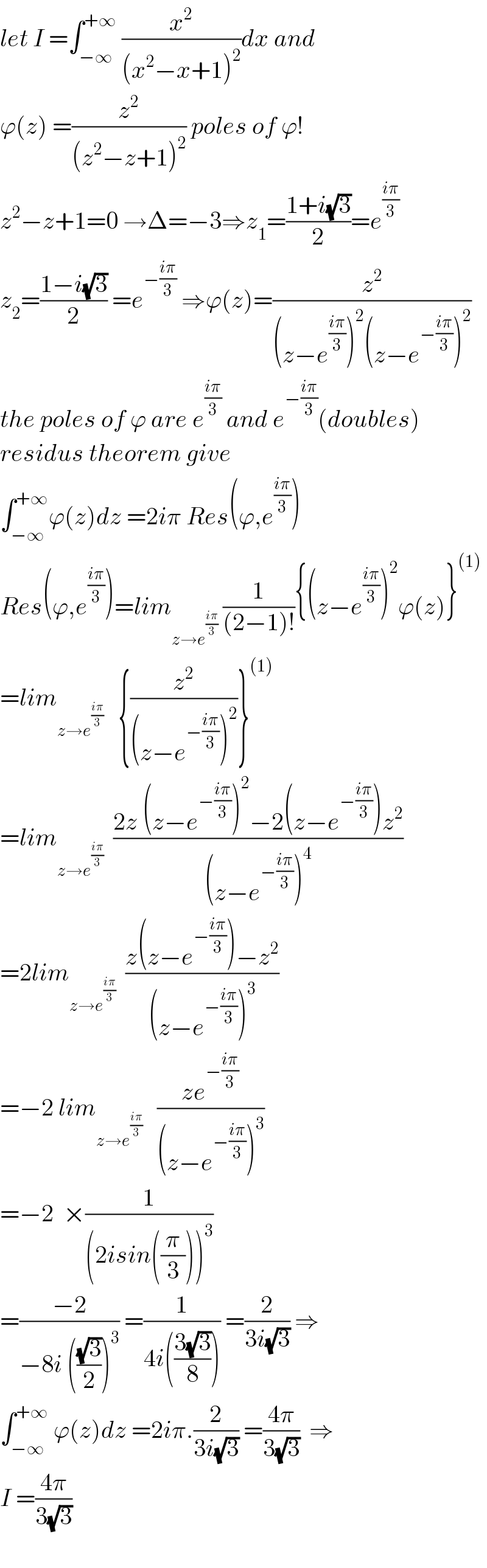
let I =∫_(−∞) ^(+∞) (x^2 /((x^2 −x+1)^2 ))dx and ϕ(z) =(z^2 /((z^2 −z+1)^2 )) poles of ϕ! z^2 −z+1=0 →Δ=−3⇒z_1 =((1+i(√3))/2)=e^((iπ)/3) z_2 =((1−i(√3))/2) =e^(−((iπ)/3)) ⇒ϕ(z)=(z^2 /((z−e^((iπ)/3) )^2 (z−e^(−((iπ)/3)) )^2 )) the poles of ϕ are e^((iπ)/3) and e^(−((iπ)/3)) (doubles) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(ϕ,e^((iπ)/3) ) Res(ϕ,e^((iπ)/3) )=lim_(z→e^((iπ)/3) ) (1/((2−1)!)){(z−e^((iπ)/3) )^2 ϕ(z)}^((1)) =lim_(z→e^((iπ)/3) ) {(z^2 /((z−e^(−((iπ)/3)) )^2 ))}^((1)) =lim_(z→e^((iπ)/3) ) ((2z (z−e^(−((iπ)/3)) )^2 −2(z−e^(−((iπ)/3)) )z^2 )/((z−e^(−((iπ)/3)) )^4 )) =2lim_(z→e^((iπ)/3) ) ((z(z−e^(−((iπ)/3)) )−z^2 )/((z−e^(−((iπ)/3)) )^3 )) =−2 lim_(z→e^((iπ)/3) ) ((ze^(−((iπ)/3)) )/((z−e^(−((iπ)/3)) )^3 )) =−2 ×(1/((2isin((π/3)))^3 )) =((−2)/(−8i (((√3)/2))^3 )) =(1/(4i(((3(√3))/8)))) =(2/(3i(√3))) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ.(2/(3i(√3))) =((4π)/(3(√3))) ⇒ I =((4π)/(3(√3)))
$${let}\:{I}\:=\int_{−\infty} ^{+\infty} \:\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:{and} \\ $$$$\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} }{\left({z}^{\mathrm{2}} −{z}+\mathrm{1}\right)^{\mathrm{2}} }\:{poles}\:{of}\:\varphi! \\ $$$${z}^{\mathrm{2}} −{z}+\mathrm{1}=\mathrm{0}\:\rightarrow\Delta=−\mathrm{3}\Rightarrow{z}_{\mathrm{1}} =\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{\frac{{i}\pi}{\mathrm{3}}} \\ $$$${z}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:={e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\Rightarrow\varphi\left({z}\right)=\frac{{z}^{\mathrm{2}} }{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} \left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} } \\ $$$${the}\:{poles}\:{of}\:\varphi\:{are}\:{e}^{\frac{{i}\pi}{\mathrm{3}}} \:{and}\:{e}^{−\frac{{i}\pi}{\mathrm{3}}} \left({doubles}\right) \\ $$$${residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right) \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{3}}} } \:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} \varphi\left({z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{3}}} } \:\:\:\left\{\frac{{z}^{\mathrm{2}} }{\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{3}}} } \:\:\frac{\mathrm{2}{z}\:\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} −\mathrm{2}\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right){z}^{\mathrm{2}} }{\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} } \\ $$$$=\mathrm{2}{lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{3}}} } \:\:\frac{{z}\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)−{z}^{\mathrm{2}} }{\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} } \\ $$$$=−\mathrm{2}\:{lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{3}}} } \:\:\:\frac{{ze}^{−\frac{{i}\pi}{\mathrm{3}}} }{\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} } \\ $$$$=−\mathrm{2}\:\:×\frac{\mathrm{1}}{\left(\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{3}}\right)\right)^{\mathrm{3}} } \\ $$$$=\frac{−\mathrm{2}}{−\mathrm{8}{i}\:\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\mathrm{4}{i}\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\right)}\:=\frac{\mathrm{2}}{\mathrm{3}{i}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi.\frac{\mathrm{2}}{\mathrm{3}{i}\sqrt{\mathrm{3}}}\:=\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\:\Rightarrow \\ $$$${I}\:=\frac{\mathrm{4}\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 11/Oct/20
(x^2 /((x^2 −x +1)^2 ))≡ ((ax+b)/((x^2 −x +1)))+ ((cx^2 +dx+e)/(x^4 −2x^3 +3x^2 −2x+1)) ⇔x^2 ≡ax^5 +(c−2a)x^4 +(3a−2b−c+d)x^3 +(3b−2a+c−d+e)x^2 + +(a−2b+d−e)x+b+e ⇔ { ((a=0)),((c−2a=0)),((3a−2b−c+d=0)),((−2a+3b+c−d+e=1)),((a−2b+d−e=0)),((b+e=0)) :} ⇔ { ((a=0)),((b=2/3=d)),((e=−2/3)),((c=1/3)) :} Hence,∫_(−∞) ^∞ (x^2 /((x^2 −x +1)^2 ))dx =(2/3)∫_(−∞) ^(+∞) (dx/(x^2 −x+1))+(1/3)∫_(−∞) ^(+∞) ((x^2 +2x−2)/((x^2 −x+1)^2 ))dx Put F=∫((x^2 +2x−2)/((x^2 −x+1)^2 ))dx.We will find F in form:F(x)=((ax^2 +bx+c)/(x^2 −x+1))+C ⇔ ((x^2 +2x−2)/(2(x^2 −x +1)^2 ))≡F′(x)=(((ax^2 +bx+c)/(x^2 −x+1)))′ =(((2ax+b)(x^2 −x+1)−(ax^2 +bx+c)(2x−1))/((x^2 −x+1)^2 )) ={2ax^3 +(b−2a)x^2 +(2a−b)x+b −[2ax^3 +(2b−a)x^2 +(2c−b)x−c]}/(x^2 −x+1)^2 =(((−a−b)x^2 +(2a−2c)x+b+c)/((x^2 −x+1)^2 )) ⇔ { ((−a−b=1)),((2a−2c=2)),((b+c=−2)) :}⇔ { ((−2b−2c=4)),((b+c=−2)) :} ⇒b=−2−c a=−b−1=1+c ⇒F(x)=(((1+c)x^2 −(2+c)x+c)/(x^2 −x+1)) =((−x−1)/(x^2 −x+1))+c+1(1).We have (2/3)∫(dx/(x^2 −x+1))=(2/3)∫(dx/((x−(1/2))^2 +(((√3)/2))^2 )) =(2/3)×(2/( (√3)))tan^(−1) (((2x−1)/( (√3))))(2)(since ∫(dx/(x^2 +a^2 ))=tan^(−1) ((x/a))) From (1)(2) and (c+1) as a constant We get: I= ∫_(−∞) ^∞ (x^2 /((x^2 −x +1)^2 ))dx =[(4/(3(√3)))tan^(−1) (((2x−1)/( (√3))))−(1/3).((x+1)/(x^2 −x+1))]_(−∞) ^(+∞) =((4(√3))/9)×(π/2)×2=((4π(√3))/9)
$$\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\:+\mathrm{1}\right)^{\mathrm{2}} }\equiv\:\:\frac{\mathrm{ax}+\mathrm{b}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\:+\mathrm{1}\right)}+\:\frac{\mathrm{cx}^{\mathrm{2}} +\mathrm{dx}+\mathrm{e}}{\mathrm{x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{3}} +\mathrm{3x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{1}} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} \equiv\mathrm{ax}^{\mathrm{5}} +\left(\mathrm{c}−\mathrm{2a}\right)\mathrm{x}^{\mathrm{4}} +\left(\mathrm{3a}−\mathrm{2b}−\mathrm{c}+\mathrm{d}\right)\mathrm{x}^{\mathrm{3}} \\ $$$$+\left(\mathrm{3b}−\mathrm{2a}+\mathrm{c}−\mathrm{d}+\mathrm{e}\right)\mathrm{x}^{\mathrm{2}} + \\ $$$$+\left(\mathrm{a}−\mathrm{2b}+\mathrm{d}−\mathrm{e}\right)\mathrm{x}+\mathrm{b}+\mathrm{e} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{a}=\mathrm{0}}\\{\mathrm{c}−\mathrm{2a}=\mathrm{0}}\\{\mathrm{3a}−\mathrm{2b}−\mathrm{c}+\mathrm{d}=\mathrm{0}}\\{−\mathrm{2a}+\mathrm{3b}+\mathrm{c}−\mathrm{d}+\mathrm{e}=\mathrm{1}}\\{\mathrm{a}−\mathrm{2b}+\mathrm{d}−\mathrm{e}=\mathrm{0}}\\{\mathrm{b}+\mathrm{e}=\mathrm{0}}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{a}=\mathrm{0}}\\{\mathrm{b}=\mathrm{2}/\mathrm{3}=\mathrm{d}}\\{\mathrm{e}=−\mathrm{2}/\mathrm{3}}\\{\mathrm{c}=\mathrm{1}/\mathrm{3}}\end{cases} \\ $$$$\mathrm{Hence},\int_{−\infty} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int_{−\infty} ^{+\infty} \frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}}\int_{−\infty} ^{+\infty} \frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{Put}\:\mathrm{F}=\int\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}.\mathrm{We}\:\mathrm{will}\:\mathrm{find}\:\mathrm{F} \\ $$$$\mathrm{in}\:\mathrm{form}:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}+\mathrm{C} \\ $$$$\Leftrightarrow\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}−\mathrm{2}}{\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\:+\mathrm{1}\right)^{\mathrm{2}} }\equiv\mathrm{F}'\left(\mathrm{x}\right)=\left(\frac{\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\right)' \\ $$$$=\frac{\left(\mathrm{2ax}+\mathrm{b}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)−\left(\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}\right)\left(\mathrm{2x}−\mathrm{1}\right)}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\left\{\mathrm{2ax}^{\mathrm{3}} +\left(\mathrm{b}−\mathrm{2a}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{2a}−\mathrm{b}\right)\mathrm{x}+\mathrm{b}\right. \\ $$$$\left.−\left[\mathrm{2ax}^{\mathrm{3}} +\left(\mathrm{2b}−\mathrm{a}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{2c}−\mathrm{b}\right)\mathrm{x}−\mathrm{c}\right]\right\}/\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\frac{\left(−\mathrm{a}−\mathrm{b}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{2a}−\mathrm{2c}\right)\mathrm{x}+\mathrm{b}+\mathrm{c}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Leftrightarrow\begin{cases}{−\mathrm{a}−\mathrm{b}=\mathrm{1}}\\{\mathrm{2a}−\mathrm{2c}=\mathrm{2}}\\{\mathrm{b}+\mathrm{c}=−\mathrm{2}}\end{cases}\Leftrightarrow\begin{cases}{−\mathrm{2b}−\mathrm{2c}=\mathrm{4}}\\{\mathrm{b}+\mathrm{c}=−\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\mathrm{b}=−\mathrm{2}−\mathrm{c} \\ $$$$\mathrm{a}=−\mathrm{b}−\mathrm{1}=\mathrm{1}+\mathrm{c} \\ $$$$\Rightarrow\mathrm{F}\left(\mathrm{x}\right)=\frac{\left(\mathrm{1}+\mathrm{c}\right)\mathrm{x}^{\mathrm{2}} −\left(\mathrm{2}+\mathrm{c}\right)\mathrm{x}+\mathrm{c}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}} \\ $$$$=\frac{−\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}+\mathrm{c}+\mathrm{1}\left(\mathrm{1}\right).\mathrm{We}\:\mathrm{have} \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{dx}}{\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\left(\mathrm{2}\right)\left(\mathrm{since}\:\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} }=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{a}}\right)\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right)\:\mathrm{and}\:\left(\mathrm{c}+\mathrm{1}\right)\:\mathrm{as}\:\mathrm{a}\:\mathrm{constant} \\ $$$$\mathrm{We}\:\mathrm{get}:\:\mathrm{I}=\:\int_{−\infty} ^{\infty} \:\:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}\:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\left[\frac{\mathrm{4}}{\mathrm{3}\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\right]_{−\infty} ^{+\infty} \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{9}}×\frac{\pi}{\mathrm{2}}×\mathrm{2}=\frac{\mathrm{4}\pi\sqrt{\mathrm{3}}}{\mathrm{9}} \\ $$
Commented by 1549442205PVT last updated on 11/Oct/20
Thank Prof.You are welcome.
$$\mathrm{Thank}\:\mathrm{Prof}.\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}. \\ $$
Commented by mathmax by abdo last updated on 11/Oct/20
thank you sir.
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *