Question Number 28158 by abdo imad last updated on 21/Jan/18
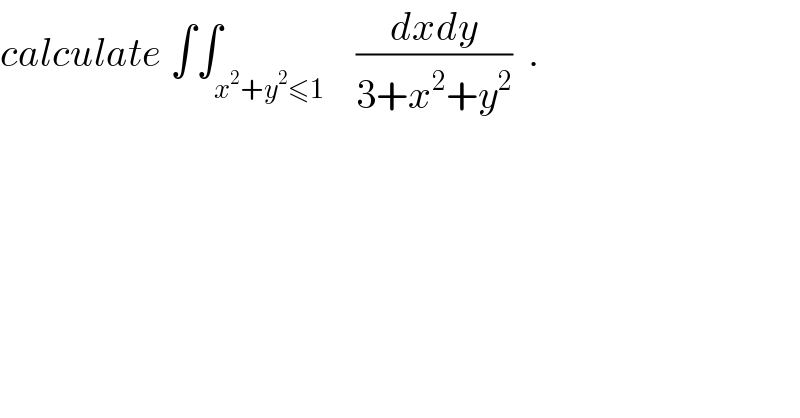
$${calculate}\:\int\int_{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \leqslant\mathrm{1}} \:\:\:\frac{{dxdy}}{\mathrm{3}+{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:. \\ $$
Answered by ajfour last updated on 21/Jan/18
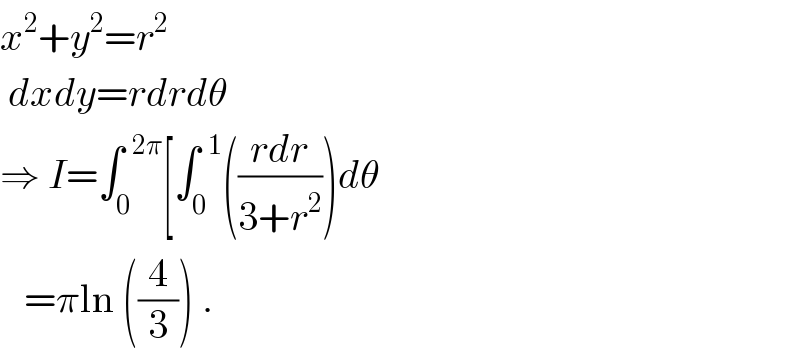
$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\:{dxdy}={rdrd}\theta\:\:\:\: \\ $$$$\Rightarrow\:{I}=\int_{\mathrm{0}} ^{\:\:\mathrm{2}\pi} \left[\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \left(\frac{{rdr}}{\mathrm{3}+{r}^{\mathrm{2}} }\right){d}\theta\right. \\ $$$$\:\:\:=\pi\mathrm{ln}\:\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\:. \\ $$
