Question Number 31085 by abdo imad last updated on 02/Mar/18
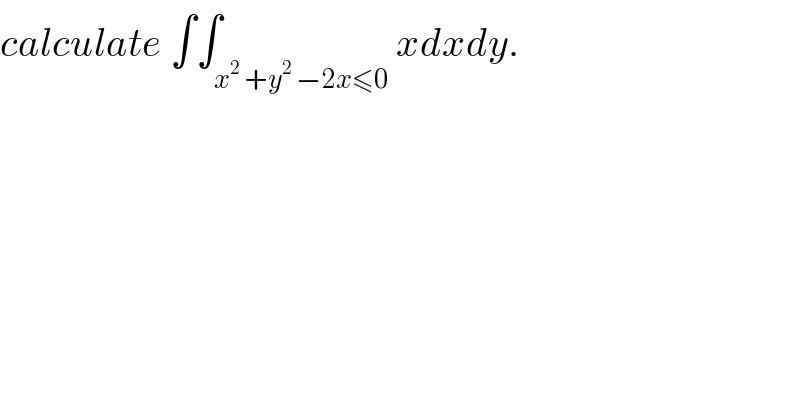
$${calculate}\:\int\int_{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:−\mathrm{2}{x}\leqslant\mathrm{0}} {xdxdy}. \\ $$
Commented by abdo imad last updated on 11/Mar/18
![let use the olar coordinates x=rcosθ and y=rsinθ x^2 +y^2 −2x ≤0 ⇔ r^2 −2rcosθ≤0 ⇔ 0<r≤2coθ due to diffeomorphisme ((−π)/2)≤θ≤(π/2) ⇒ I=∫∫_(−(π/2)≤θ≤(π/2) and 0<r≤2cosθ) rcosθ rdrdθ =∫_(−(π/2)) ^(π/2) ( ∫_0 ^(2cosθ) r^2 dr)cosθ dθ but ∫_0 ^(2cosθ) r^2 dr=[(1/3)r^3 ]_0 ^(2cosθ) =(8/3) cos^3 θ ⇒ I= (8/3) ∫_(−(π/2)) ^(π/2) cos^4 dθ =((16)/3) ∫_0 ^(π/2) (((1+cos(2θ))^2 )/4)dθ =(4/3)∫_0 ^(π/2) (1+2cos(2θ)+((1+cos(4θ))/2))dθ =(4/3)(π/2) +(8/3)∫_0 ^(π/2) cos(2θ)dθ +(2/3) (π/2) +(2/3) ∫_0 ^(π/2) cos(4θ)dθ =((2π)/3) +0 +(π/3) +0 =π ⇒ I=π.](https://www.tinkutara.com/question/Q31622.png)
$${let}\:{use}\:{the}\:{olar}\:{coordinates}\:\:{x}={rcos}\theta\:{and}\:{y}={rsin}\theta \\ $$$${x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:−\mathrm{2}{x}\:\leqslant\mathrm{0}\:\Leftrightarrow\:{r}^{\mathrm{2}} \:−\mathrm{2}{rcos}\theta\leqslant\mathrm{0}\:\Leftrightarrow\:\mathrm{0}<{r}\leqslant\mathrm{2}{co}\theta\:{due}\:{to} \\ $$$${diffeomorphisme}\:\:\frac{−\pi}{\mathrm{2}}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${I}=\int\int_{−\frac{\pi}{\mathrm{2}}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}\:{and}\:\mathrm{0}<{r}\leqslant\mathrm{2}{cos}\theta} {rcos}\theta\:{rdrd}\theta \\ $$$$=\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \left(\:\int_{\mathrm{0}} ^{\mathrm{2}{cos}\theta} \:{r}^{\mathrm{2}} {dr}\right){cos}\theta\:{d}\theta\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}{cos}\theta} \:{r}^{\mathrm{2}} {dr}=\left[\frac{\mathrm{1}}{\mathrm{3}}{r}^{\mathrm{3}} \right]_{\mathrm{0}} ^{\mathrm{2}{cos}\theta} =\frac{\mathrm{8}}{\mathrm{3}}\:{cos}^{\mathrm{3}} \theta\:\Rightarrow \\ $$$${I}=\:\frac{\mathrm{8}}{\mathrm{3}}\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{4}} {d}\theta\:=\frac{\mathrm{16}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\left(\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)\right)^{\mathrm{2}} }{\mathrm{4}}{d}\theta \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{1}+\mathrm{2}{cos}\left(\mathrm{2}\theta\right)+\frac{\mathrm{1}+{cos}\left(\mathrm{4}\theta\right)}{\mathrm{2}}\right){d}\theta \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{8}}{\mathrm{3}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}\theta\right){d}\theta\:\:+\frac{\mathrm{2}}{\mathrm{3}}\:\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{2}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{4}\theta\right){d}\theta \\ $$$$=\frac{\mathrm{2}\pi}{\mathrm{3}}\:+\mathrm{0}\:+\frac{\pi}{\mathrm{3}}\:+\mathrm{0}\:=\pi\:\Rightarrow\:{I}=\pi. \\ $$
