Question Number 53781 by maxmathsup by imad last updated on 25/Jan/19
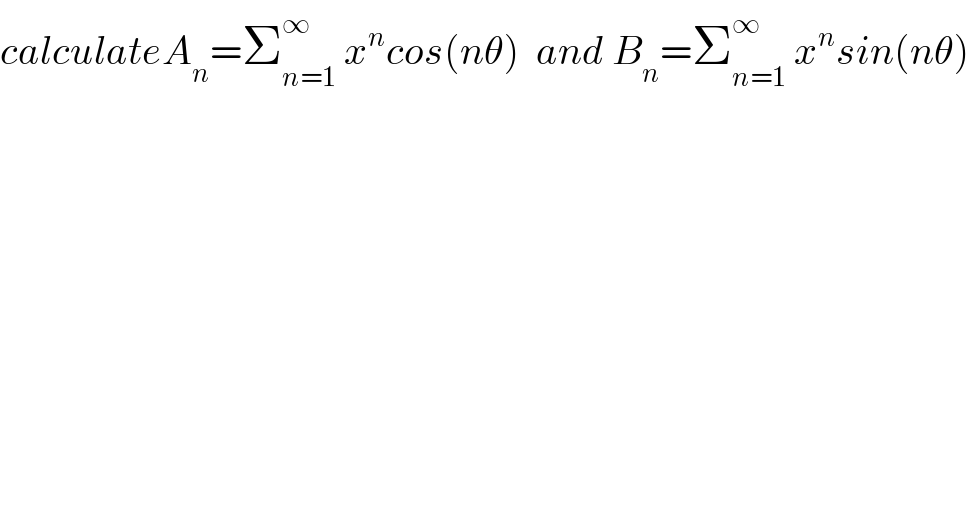
$${calculateA}_{{n}} =\sum_{{n}=\mathrm{1}} ^{\infty} \:{x}^{{n}} {cos}\left({n}\theta\right)\:\:{and}\:{B}_{{n}} =\sum_{{n}=\mathrm{1}} ^{\infty} \:{x}^{{n}} {sin}\left({n}\theta\right) \\ $$
Commented by maxmathsup by imad last updated on 26/Jan/19
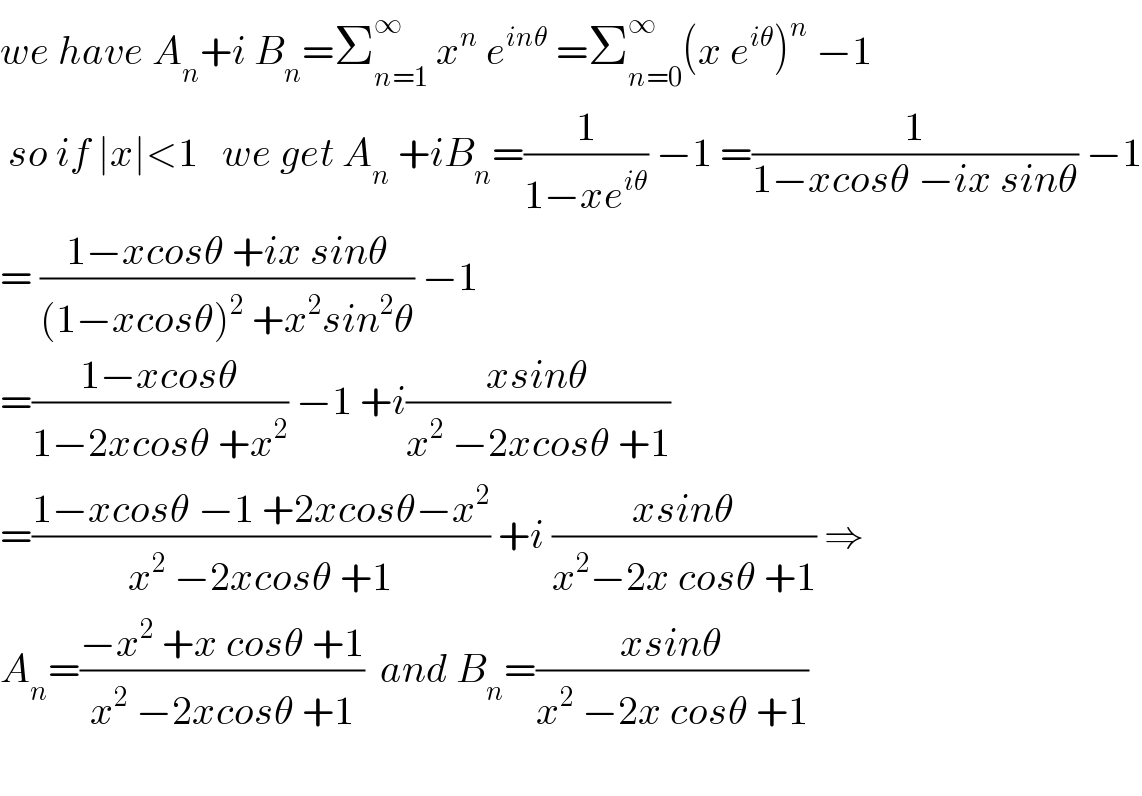
$${we}\:{have}\:{A}_{{n}} +{i}\:{B}_{{n}} =\sum_{{n}=\mathrm{1}} ^{\infty} \:{x}^{{n}} \:{e}^{{in}\theta} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \left({x}\:{e}^{{i}\theta} \right)^{{n}} \:−\mathrm{1} \\ $$$$\:{so}\:{if}\:\mid{x}\mid<\mathrm{1}\:\:\:{we}\:{get}\:{A}_{{n}} \:+{iB}_{{n}} =\frac{\mathrm{1}}{\mathrm{1}−{xe}^{{i}\theta} }\:−\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{1}−{xcos}\theta\:−{ix}\:{sin}\theta}\:−\mathrm{1} \\ $$$$=\:\frac{\mathrm{1}−{xcos}\theta\:+{ix}\:{sin}\theta}{\left(\mathrm{1}−{xcos}\theta\right)^{\mathrm{2}} \:+{x}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}\:−\mathrm{1} \\ $$$$=\frac{\mathrm{1}−{xcos}\theta}{\mathrm{1}−\mathrm{2}{xcos}\theta\:+{x}^{\mathrm{2}} }\:−\mathrm{1}\:+{i}\frac{{xsin}\theta}{{x}^{\mathrm{2}} \:−\mathrm{2}{xcos}\theta\:+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}−{xcos}\theta\:−\mathrm{1}\:+\mathrm{2}{xcos}\theta−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} \:−\mathrm{2}{xcos}\theta\:+\mathrm{1}}\:+{i}\:\frac{{xsin}\theta}{{x}^{\mathrm{2}} −\mathrm{2}{x}\:{cos}\theta\:+\mathrm{1}}\:\Rightarrow \\ $$$${A}_{{n}} =\frac{−{x}^{\mathrm{2}} \:+{x}\:{cos}\theta\:+\mathrm{1}}{{x}^{\mathrm{2}} \:−\mathrm{2}{xcos}\theta\:+\mathrm{1}}\:\:{and}\:{B}_{{n}} =\frac{{xsin}\theta}{{x}^{\mathrm{2}} \:−\mathrm{2}{x}\:{cos}\theta\:+\mathrm{1}} \\ $$$$ \\ $$
Answered by Smail last updated on 26/Jan/19
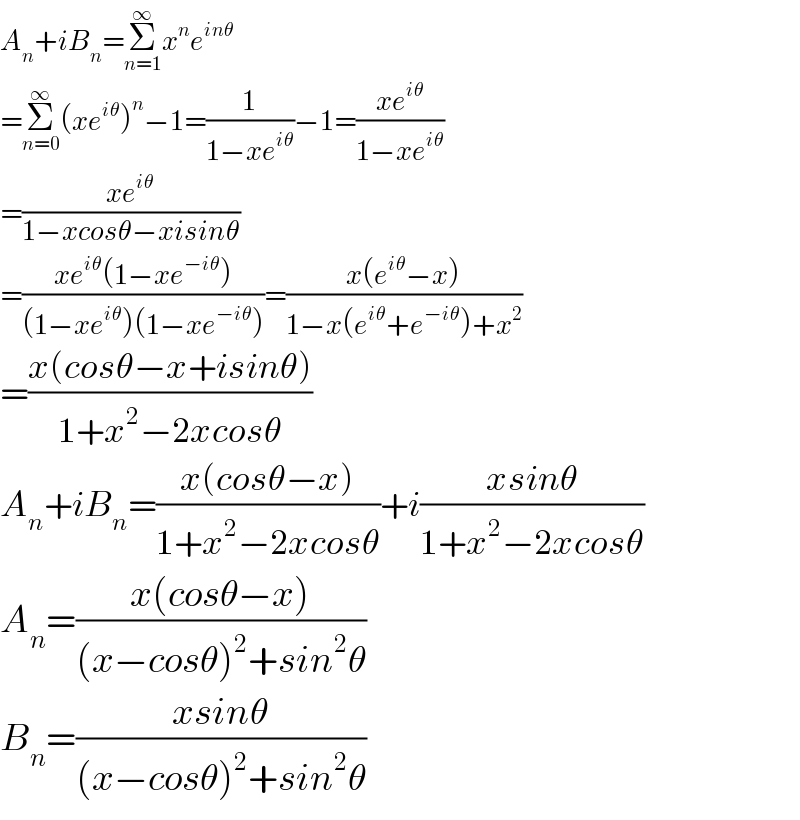
$${A}_{{n}} +{iB}_{{n}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{n}} {e}^{{in}\theta} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({xe}^{{i}\theta} \right)^{{n}} −\mathrm{1}=\frac{\mathrm{1}}{\mathrm{1}−{xe}^{{i}\theta} }−\mathrm{1}=\frac{{xe}^{{i}\theta} }{\mathrm{1}−{xe}^{{i}\theta} } \\ $$$$=\frac{{xe}^{{i}\theta} }{\mathrm{1}−{xcos}\theta−{xisin}\theta} \\ $$$$=\frac{{xe}^{{i}\theta} \left(\mathrm{1}−{xe}^{−{i}\theta} \right)}{\left(\mathrm{1}−{xe}^{{i}\theta} \right)\left(\mathrm{1}−{xe}^{−{i}\theta} \right)}=\frac{{x}\left({e}^{{i}\theta} −{x}\right)}{\mathrm{1}−{x}\left({e}^{{i}\theta} +{e}^{−{i}\theta} \right)+{x}^{\mathrm{2}} } \\ $$$$=\frac{{x}\left({cos}\theta−{x}+{isin}\theta\right)}{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{xcos}\theta} \\ $$$${A}_{{n}} +{iB}_{{n}} =\frac{{x}\left({cos}\theta−{x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{xcos}\theta}+{i}\frac{{xsin}\theta}{\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{2}{xcos}\theta} \\ $$$${A}_{{n}} =\frac{{x}\left({cos}\theta−{x}\right)}{\left({x}−{cos}\theta\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} \theta} \\ $$$${B}_{{n}} =\frac{{xsin}\theta}{\left({x}−{cos}\theta\right)^{\mathrm{2}} +{sin}^{\mathrm{2}} \theta} \\ $$
