Menu Close

calculatef-a-1-a-x-2-arctan-a-x-dx-2-calculate-1-1-2-x-2-arctan-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 55282 by Abdo msup. last updated on 20/Feb/19
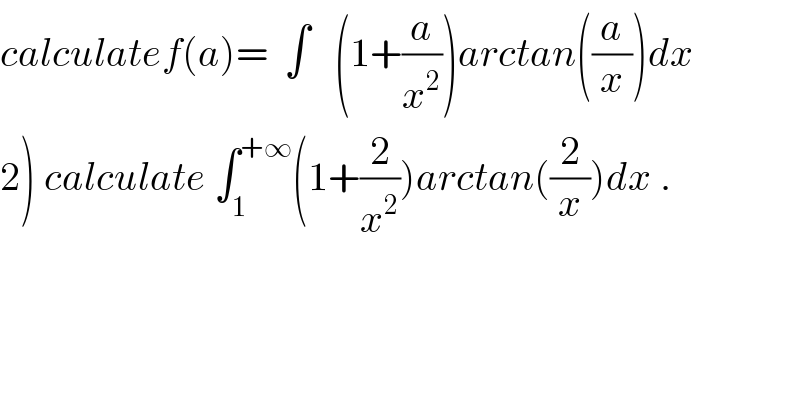
calculatef(a)= ∫ (1+(a/x^2 ))arctan((a/x))dx 2) calculate ∫_1 ^(+∞) (1+(2/x^2 ))arctan((2/x))dx .
$${calculatef}\left({a}\right)=\:\:\int\:\:\:\left(\mathrm{1}+\frac{{a}}{{x}^{\mathrm{2}} }\right){arctan}\left(\frac{{a}}{{x}}\right){dx} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{1}} ^{+\infty} \left(\mathrm{1}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right){arctan}\left(\frac{\mathrm{2}}{{x}}\right){dx}\:. \\ $$
Commented by maxmathsup by imad last updated on 24/Feb/19
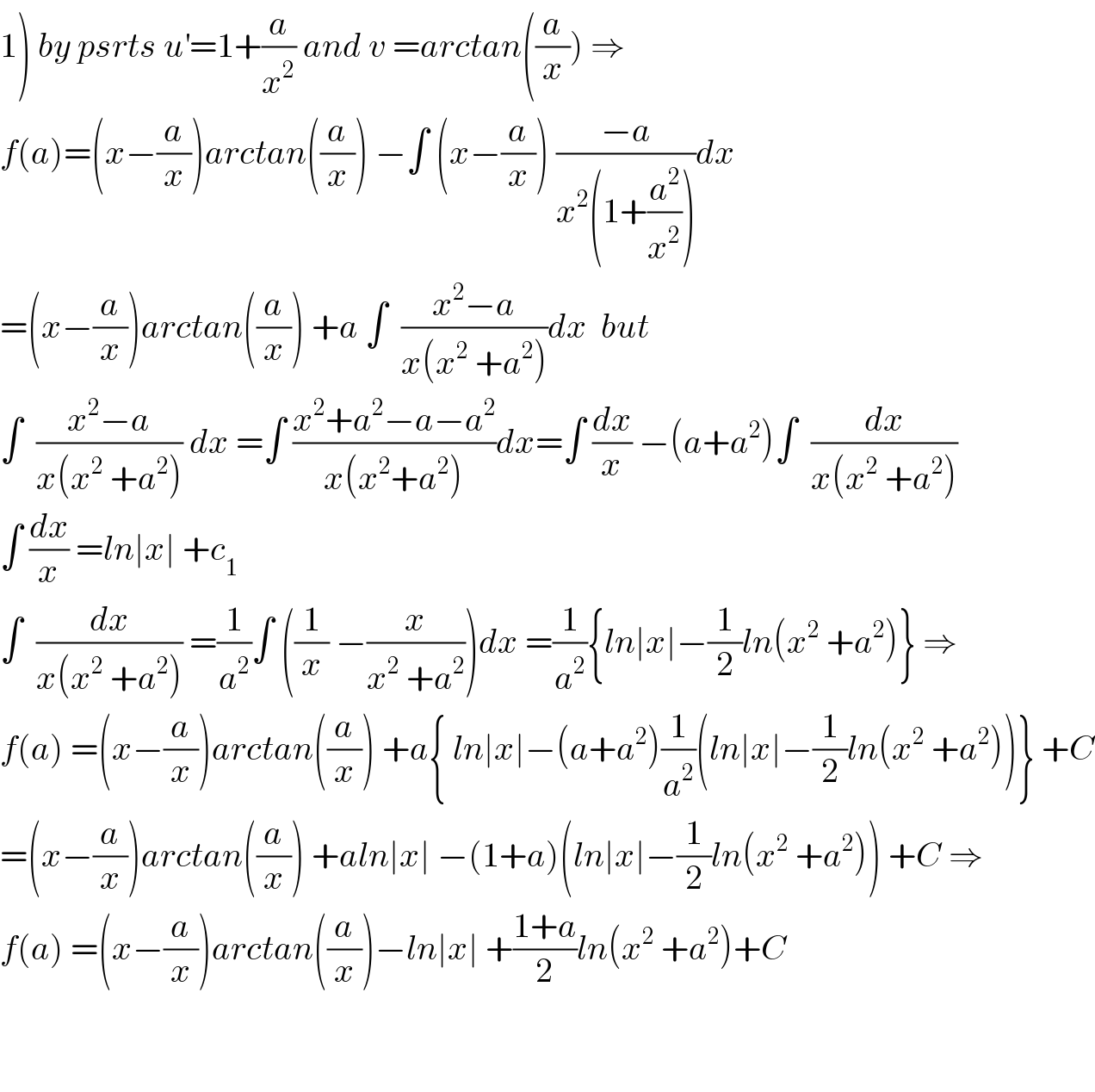
1) by psrts u^′ =1+(a/x^2 ) and v =arctan((a/x)) ⇒ f(a)=(x−(a/x))arctan((a/x)) −∫ (x−(a/x)) ((−a)/(x^2 (1+(a^2 /x^2 ))))dx =(x−(a/x))arctan((a/x)) +a ∫ ((x^2 −a)/(x(x^2 +a^2 )))dx but ∫ ((x^2 −a)/(x(x^2 +a^2 ))) dx =∫ ((x^2 +a^2 −a−a^2 )/(x(x^2 +a^2 )))dx=∫ (dx/x) −(a+a^2 )∫ (dx/(x(x^2 +a^2 ))) ∫ (dx/x) =ln∣x∣ +c_1 ∫ (dx/(x(x^2 +a^2 ))) =(1/a^2 )∫ ((1/x) −(x/(x^2 +a^2 )))dx =(1/a^2 ){ln∣x∣−(1/2)ln(x^2 +a^2 )} ⇒ f(a) =(x−(a/x))arctan((a/x)) +a{ ln∣x∣−(a+a^2 )(1/a^2 )(ln∣x∣−(1/2)ln(x^2 +a^2 ))} +C =(x−(a/x))arctan((a/x)) +aln∣x∣ −(1+a)(ln∣x∣−(1/2)ln(x^2 +a^2 )) +C ⇒ f(a) =(x−(a/x))arctan((a/x))−ln∣x∣ +((1+a)/2)ln(x^2 +a^2 )+C
$$\left.\mathrm{1}\right)\:{by}\:{psrts}\:{u}^{'} =\mathrm{1}+\frac{{a}}{{x}^{\mathrm{2}} }\:{and}\:{v}\:={arctan}\left(\frac{{a}}{{x}}\right)\:\Rightarrow \\ $$$${f}\left({a}\right)=\left({x}−\frac{{a}}{{x}}\right){arctan}\left(\frac{{a}}{{x}}\right)\:−\int\:\left({x}−\frac{{a}}{{x}}\right)\:\frac{−{a}}{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}{dx} \\ $$$$=\left({x}−\frac{{a}}{{x}}\right){arctan}\left(\frac{{a}}{{x}}\right)\:+{a}\:\int\:\:\frac{{x}^{\mathrm{2}} −{a}}{{x}\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)}{dx}\:\:{but}\: \\ $$$$\int\:\:\frac{{x}^{\mathrm{2}} −{a}}{{x}\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)}\:{dx}\:=\int\:\frac{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} −{a}−{a}^{\mathrm{2}} }{{x}\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}{dx}=\int\:\frac{{dx}}{{x}}\:−\left({a}+{a}^{\mathrm{2}} \right)\int\:\:\frac{{dx}}{{x}\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)} \\ $$$$\int\:\frac{{dx}}{{x}}\:={ln}\mid{x}\mid\:+{c}_{\mathrm{1}} \\ $$$$\int\:\:\frac{{dx}}{{x}\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int\:\left(\frac{\mathrm{1}}{{x}}\:−\frac{{x}}{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }\right){dx}\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\left\{{ln}\mid{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)\right\}\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\left({x}−\frac{{a}}{{x}}\right){arctan}\left(\frac{{a}}{{x}}\right)\:+{a}\left\{\:{ln}\mid{x}\mid−\left({a}+{a}^{\mathrm{2}} \right)\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\left({ln}\mid{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)\right)\right\}\:+{C} \\ $$$$=\left({x}−\frac{{a}}{{x}}\right){arctan}\left(\frac{{a}}{{x}}\right)\:+{aln}\mid{x}\mid\:−\left(\mathrm{1}+{a}\right)\left({ln}\mid{x}\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)\right)\:+{C}\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\left({x}−\frac{{a}}{{x}}\right){arctan}\left(\frac{{a}}{{x}}\right)−{ln}\mid{x}\mid\:+\frac{\mathrm{1}+{a}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} \right)+{C} \\ $$$$ \\ $$$$ \\ $$
Answered by Smail last updated on 22/Feb/19
f(a)=∫(arctan((a/x))+((a×arctan((a/x)))/x^2 ))dx =∫arctan((a/x))dx+a∫((arctan((a/x)))/x^2 )dx By parts u=arctan(a/x)⇒u′=((−a)/(x^2 +a^2 )) v′=1⇒v=x f(a)=x×arctan((a/x))+a∫(x/(x^2 +a^2 ))dx+a∫((arctan(a/x))/x^2 )dx+c_1 t=(a/x)⇒−dt=((adx)/x^2 ) =x×arctan((a/x))+(a/2)ln(x^2 +a^2 )−∫arctan(t)dt+c_2 By parts u=arctant⇒u′=(1/(1+t^2 )) v′=1⇒v=t f(a)=x×arctan((a/x))+(a/2)ln(x^2 +a^2 )−t×arctant+(1/2)ln(1+t^2 )+C =arctan((a/x))(x−(a/x))+(a/2)ln(x^2 +a^2 )+(1/2)ln(((x^2 +a^2 )/x^2 ))+C f(a)=(((x^2 −a)/x))arctan((a/x))+(((a+1))/2)ln(x^2 +a^2 )−lnx+C
$${f}\left({a}\right)=\int\left({arctan}\left(\frac{{a}}{{x}}\right)+\frac{{a}×{arctan}\left(\frac{{a}}{{x}}\right)}{{x}^{\mathrm{2}} }\right){dx} \\ $$$$=\int{arctan}\left(\frac{{a}}{{x}}\right){dx}+{a}\int\frac{{arctan}\left(\frac{{a}}{{x}}\right)}{{x}^{\mathrm{2}} }{dx} \\ $$$${By}\:{parts} \\ $$$${u}={arctan}\frac{{a}}{{x}}\Rightarrow{u}'=\frac{−{a}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} } \\ $$$${v}'=\mathrm{1}\Rightarrow{v}={x} \\ $$$${f}\left({a}\right)={x}×{arctan}\left(\frac{{a}}{{x}}\right)+{a}\int\frac{{x}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}+{a}\int\frac{{arctan}\left({a}/{x}\right)}{{x}^{\mathrm{2}} }{dx}+{c}_{\mathrm{1}} \\ $$$${t}=\frac{{a}}{{x}}\Rightarrow−{dt}=\frac{{adx}}{{x}^{\mathrm{2}} } \\ $$$$={x}×{arctan}\left(\frac{{a}}{{x}}\right)+\frac{{a}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)−\int{arctan}\left({t}\right){dt}+{c}_{\mathrm{2}} \\ $$$${By}\:{parts}\: \\ $$$${u}={arctant}\Rightarrow{u}'=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${v}'=\mathrm{1}\Rightarrow{v}={t} \\ $$$${f}\left({a}\right)={x}×{arctan}\left(\frac{{a}}{{x}}\right)+\frac{{a}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)−{t}×{arctant}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)+{C} \\ $$$$={arctan}\left(\frac{{a}}{{x}}\right)\left({x}−\frac{{a}}{{x}}\right)+\frac{{a}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)+{C} \\ $$$${f}\left({a}\right)=\left(\frac{{x}^{\mathrm{2}} −{a}}{{x}}\right){arctan}\left(\frac{{a}}{{x}}\right)+\frac{\left({a}+\mathrm{1}\right)}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)−{lnx}+{C} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 24/Feb/19
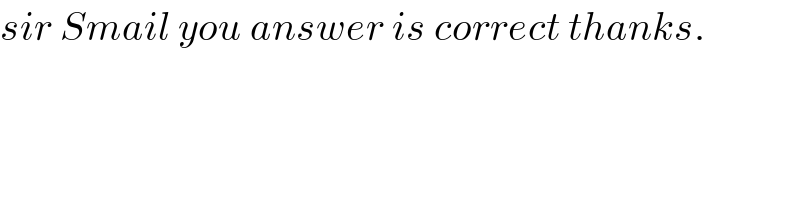
sir Smail you answer is correct thanks.
$${sir}\:{Smail}\:{you}\:{answer}\:{is}\:{correct}\:{thanks}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *