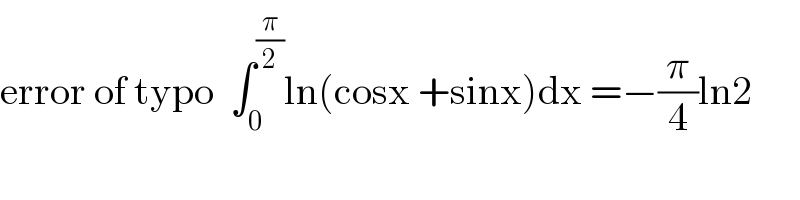Question Number 96495 by abdomathmax last updated on 01/Jun/20
$$\mathrm{calculateI}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cosx}\:+\mathrm{sinx}\right)\mathrm{dx} \\ $$$$\mathrm{and}\:\mathrm{J}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cosx}−\mathrm{sinx}\right)\mathrm{dx} \\ $$
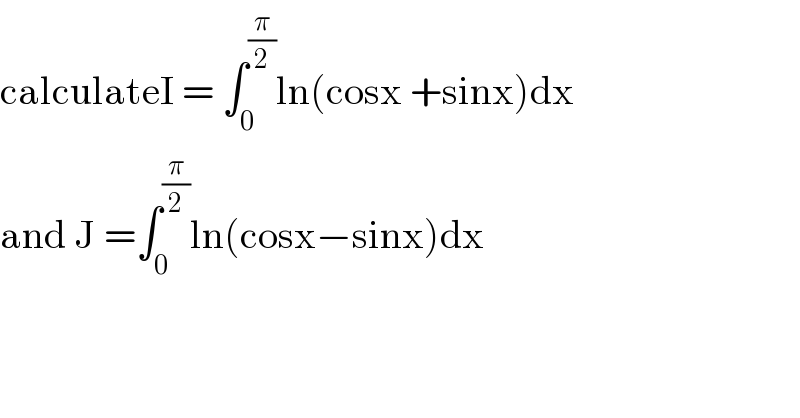
Answered by Sourav mridha last updated on 02/Jun/20
![J−I=∫_0 ^(𝛑/2) ln[tan((𝛑/4)−x)]dx...(i) and also J−I=∫_0 ^(𝛑/2) ln[cot((𝛑/4)−x)]dx .........(ii) (i)+(ii)we get..J−I=0,J=I....(g) now J+I=∫_0 ^(𝛑/2) ln(cos2x)dx...(v) now 2x=t,then 2J=(1/2)∫_0 ^𝛑 ln(cost)dt we can also write this as −− 2J=∫_0 ^(𝛑/2) ln(cost)dt....(a) so, 2J=∫_0 ^(𝛑/2) ln(sint)dt....(b) (a)+(b) 4J=(𝛑/2)ln((1/2))+∫_0 ^(𝛑/2) ln(sin(2t))dt by apply: the same approch like eq^n (v)we get,∫_0 ^(π/2) ln(sin2t)dt=2J so,4J=(𝛑/2)ln((1/2))+2J so ,2J=(𝛑/2)ln((1/2)) now from (g) I=J=(𝛑/4)ln((1/2))](https://www.tinkutara.com/question/Q96512.png)
$$\boldsymbol{{J}}−\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{{ln}}\left[\boldsymbol{{tan}}\left(\frac{\boldsymbol{\pi}}{\mathrm{4}}−\boldsymbol{{x}}\right)\right]\boldsymbol{{dx}}…\left(\boldsymbol{{i}}\right) \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{also}}\:\boldsymbol{{J}}−{I}=\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{{ln}}\left[\boldsymbol{{cot}}\left(\frac{\boldsymbol{\pi}}{\mathrm{4}}−\boldsymbol{{x}}\right)\right]\boldsymbol{{dx}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:………\left(\boldsymbol{{ii}}\right) \\ $$$$\left(\boldsymbol{{i}}\right)+\left(\boldsymbol{{ii}}\right)\boldsymbol{{we}}\:\boldsymbol{{get}}..\boldsymbol{{J}}−{I}=\mathrm{0},\boldsymbol{{J}}=\boldsymbol{{I}}….\left(\boldsymbol{{g}}\right) \\ $$$$\boldsymbol{{now}}\:\mathrm{J}+\boldsymbol{{I}}=\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{{ln}}\left(\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{x}}\right)\boldsymbol{{dx}}…\left(\boldsymbol{{v}}\right) \\ $$$$\boldsymbol{{now}}\:\mathrm{2}\boldsymbol{{x}}=\boldsymbol{{t}},\boldsymbol{{then}} \\ $$$$\mathrm{2}\boldsymbol{{J}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\boldsymbol{\pi}} \boldsymbol{{ln}}\left(\boldsymbol{{cost}}\right)\boldsymbol{{dt}}\:\boldsymbol{{we}}\:\boldsymbol{{can}}\:\boldsymbol{{also}} \\ $$$$\boldsymbol{{write}}\:\boldsymbol{{this}}\:\boldsymbol{{as}}\:−− \\ $$$$\mathrm{2}\boldsymbol{{J}}=\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{{ln}}\left(\boldsymbol{{cost}}\right)\boldsymbol{{dt}}….\left(\boldsymbol{{a}}\right) \\ $$$$\boldsymbol{{so}},\:\mathrm{2}\boldsymbol{{J}}=\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{{ln}}\left(\boldsymbol{{sint}}\right)\boldsymbol{{dt}}….\left(\boldsymbol{{b}}\right) \\ $$$$\left(\boldsymbol{{a}}\right)+\left(\boldsymbol{{b}}\right)\:\mathrm{4J}=\frac{\boldsymbol{\pi}}{\mathrm{2}}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{{ln}}\left(\boldsymbol{{sin}}\left(\mathrm{2}\boldsymbol{{t}}\right)\right)\boldsymbol{{dt}} \\ $$$$\boldsymbol{{by}}\:\boldsymbol{{apply}}:\:\mathrm{the}\:\boldsymbol{{same}}\:\boldsymbol{{approch}}\:\boldsymbol{{like}}\: \\ $$$$\boldsymbol{{eq}}^{\boldsymbol{{n}}} \:\left(\boldsymbol{{v}}\right)\boldsymbol{{we}}\:\boldsymbol{{get}},\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \boldsymbol{{ln}}\left(\boldsymbol{{sin}}\mathrm{2}\boldsymbol{{t}}\right)\boldsymbol{{dt}}=\mathrm{2}\boldsymbol{{J}} \\ $$$$\:\mathrm{so},\mathrm{4}\boldsymbol{{J}}=\frac{\boldsymbol{\pi}}{\mathrm{2}}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}\boldsymbol{{J}} \\ $$$$\mathrm{so}\:,\mathrm{2}\boldsymbol{{J}}=\frac{\boldsymbol{\pi}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{now}\:\boldsymbol{{from}}\:\left(\boldsymbol{{g}}\right)\:\boldsymbol{{I}}=\boldsymbol{{J}}=\frac{\boldsymbol{\pi}}{\mathrm{4}}\boldsymbol{{ln}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
Commented by abdomathmax last updated on 02/Jun/20
$$\mathrm{thanks}\:\mathrm{sir}. \\ $$
Commented by Sourav mridha last updated on 02/Jun/20
welcome....
Answered by mathmax by abdo last updated on 02/Jun/20
![let f(a) =∫_0 ^(π/2) ln(cosx +asinx)dx we have f^′ (a) =∫_0 ^(π/2) ((sinx)/(cosx +asinx))dx =∫_0 ^(π/2) (dx/(a +(1/(tanx)))) =_(tanx =u) ∫_0 ^∞ (du/((1+u^2 )(a+(1/u)))) =∫_0 ^∞ ((udu)/((au+1)(u^2 +1))) let decompose F(u) =(u/((au+1)(u^2 +1))) ⇒F(u) =(α/(au+1)) +((βu +λ)/(u^2 +1)) α =((−1)/(a((1/a^2 )+1))) =((−a^2 )/(a(1+a^2 ))) =((−a)/(1+a^2 )) lim_(u→+∞) uF(u) =0 =(α/a) +β ⇒β =−(α/a) =(1/(1+a^2 )) F(0) =0 =α +λ ⇒λ =(a/(1+a^2 )) ⇒F(u) =−(a/((1+a^2 )(au+1))) +(1/(1+a^2 ))×((u+a)/(u^2 +1)) ⇒∫_0 ^∞ F(u)du =−(a/(1+a^2 ))∫_0 ^∞ (du/(au+1)) +(1/(2(1+a^2 )))∫_0 ^∞ ((2u)/(u^2 +1)) +(a/(1+a^2 )) ∫_0 ^∞ (du/(u^2 +1)) =(1/(1+a^2 ))[ln(√(u^2 +1))−ln(au+1)]_0 ^∞ +((πa)/(2(1+a^2 ))) =(1/(1+a^2 ))[ln(((√(1+u^2 ))/(au +1)))]_0 ^∞ +((πa)/(2(1+a^2 ))) =−((ln(a))/(1+a^2 )) +((πa)/(2(1+a^2 ))) ⇒ f(a) =−∫_0 ^a ((lnt)/(1+t^2 ))dt +(π/4)ln(1+a^2 ) +c but f(0) =c =−(π/2)ln(2) ⇒f(a) =(π/4)ln(1+a^2 )−(π/2)ln(2)−∫_0 ^a ((lnt)/(1+t^2 ))dt ∫_0 ^(π/2) ln(cosx +sinx)dx =f(1) =(π/4)ln(2)−(π/2)ln(2)−∫_0 ^1 ((lnt)/(1+t^2 ))dt (→t =tanθ) =−(π/4)ln(2)−∫_0 ^(π/2) ln(tanθ)dθ =−(π/4)ln(2)−0 (because ∫_0 ^(π/2) ln(cosθ)dθ=∫_0 ^(π/2) ln(sinθ)dθ)⇒ ⇒∫_0 ^(π/2) ln(cosx −sinx)dx =−(π/4)ln(2)](https://www.tinkutara.com/question/Q96560.png)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{cosx}\:+\mathrm{asinx}\right)\mathrm{dx}\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sinx}}{\mathrm{cosx}\:+\mathrm{asinx}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{dx}}{\mathrm{a}\:+\frac{\mathrm{1}}{\mathrm{tanx}}}\:=_{\mathrm{tanx}\:=\mathrm{u}} \:\:\:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{a}+\frac{\mathrm{1}}{\mathrm{u}}\right)}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{udu}}{\left(\mathrm{au}+\mathrm{1}\right)\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{u}}{\left(\mathrm{au}+\mathrm{1}\right)\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\alpha}{\mathrm{au}+\mathrm{1}}\:+\frac{\beta\mathrm{u}\:+\lambda}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\alpha\:=\frac{−\mathrm{1}}{\mathrm{a}\left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{2}} }+\mathrm{1}\right)}\:=\frac{−\mathrm{a}^{\mathrm{2}} }{\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\:=\frac{−\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{lim}_{\mathrm{u}\rightarrow+\infty} \:\mathrm{uF}\left(\mathrm{u}\right)\:=\mathrm{0}\:=\frac{\alpha}{\mathrm{a}}\:+\beta\:\Rightarrow\beta\:=−\frac{\alpha}{\mathrm{a}}\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} } \\ $$$$\mathrm{F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=\alpha\:+\lambda\:\Rightarrow\lambda\:=\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:\Rightarrow\mathrm{F}\left(\mathrm{u}\right)\:=−\frac{\mathrm{a}}{\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{au}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }×\frac{\mathrm{u}+\mathrm{a}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\mathrm{F}\left(\mathrm{u}\right)\mathrm{du}\:=−\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{du}}{\mathrm{au}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2u}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\left[\mathrm{ln}\sqrt{\mathrm{u}^{\mathrm{2}} +\mathrm{1}}−\mathrm{ln}\left(\mathrm{au}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\infty} \:+\frac{\pi\mathrm{a}}{\mathrm{2}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\left[\mathrm{ln}\left(\frac{\sqrt{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}{\mathrm{au}\:+\mathrm{1}}\right)\right]_{\mathrm{0}} ^{\infty} \:+\frac{\pi\mathrm{a}}{\mathrm{2}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\:=−\frac{\mathrm{ln}\left(\mathrm{a}\right)}{\mathrm{1}+\mathrm{a}^{\mathrm{2}} }\:+\frac{\pi\mathrm{a}}{\mathrm{2}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=−\int_{\mathrm{0}} ^{\mathrm{a}} \:\:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:+\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)\:+\mathrm{c}\:\mathrm{but} \\ $$$$\mathrm{f}\left(\mathrm{0}\right)\:=\mathrm{c}\:=−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)\:\Rightarrow\mathrm{f}\left(\mathrm{a}\right)\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{cosx}\:+\mathrm{sinx}\right)\mathrm{dx}\:=\mathrm{f}\left(\mathrm{1}\right)\:=\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\frac{\pi}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\left(\rightarrow\mathrm{t}\:=\mathrm{tan}\theta\right) \\ $$$$=−\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{tan}\theta\right)\mathrm{d}\theta\:=−\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{0}\:\left(\mathrm{because}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{cos}\theta\right)\mathrm{d}\theta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}\theta\right)\mathrm{d}\theta\right)\Rightarrow \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{cosx}\:−\mathrm{sinx}\right)\mathrm{dx}\:=−\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 02/Jun/20
$$\mathrm{error}\:\mathrm{of}\:\mathrm{typo}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cosx}\:+\mathrm{sinx}\right)\mathrm{dx}\:=−\frac{\pi}{\mathrm{4}}\mathrm{ln2} \\ $$