Question Number 100514 by mathmax by abdo last updated on 27/Jun/20
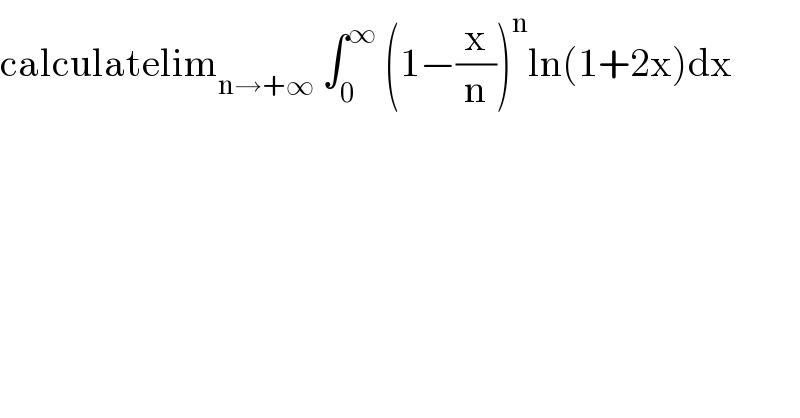
$$\mathrm{calculatelim}_{\mathrm{n}\rightarrow+\infty} \:\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{n}}\right)^{\mathrm{n}} \mathrm{ln}\left(\mathrm{1}+\mathrm{2x}\right)\mathrm{dx} \\ $$
Answered by mathmax by abdo last updated on 27/Jun/20
![A_n =∫_0 ^∞ (1−(x/n))^n ln(2x+1)dx =∫_R (1−(x/n))^n ln(2x+1)χ_([0,+∞[) (x)dx =∫_R f_n (x)dx with f_n (x) =(1−(x/n))^n ln(2x+1) f_n →^(cs) f(x) =e^(−x) ln(2x+1) and ∣f_n ∣ ≤f(x) integrable on [0,+∞[ tbeorem of convegence dominee give lim_(n→+∞) A_n =∫_0 ^∞ e^(−x) ln(2x+1)dx =L by parts L =[−e^(−x) ln(2x+1)]_0 ^(+∞) +∫_0 ^∞ e^(−x) (2/(2x+1))dx =2 ∫_0 ^∞ (e^(−x) /(2x+1))dx =_(2x+1=t) 2∫_1 ^(+∞) (e^(−(((t−1)/2))) /t)×(dt/2) =(√e)∫_1 ^(+∞) (e^(−(t/2)) /t)dt...be continued...](https://www.tinkutara.com/question/Q100577.png)
$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{n}}\right)^{\mathrm{n}} \mathrm{ln}\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{dx}\:=\int_{\mathrm{R}} \left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{n}}\right)^{\mathrm{n}} \mathrm{ln}\left(\mathrm{2x}+\mathrm{1}\right)\chi_{\left[\mathrm{0},+\infty\left[\right.\right.} \left(\mathrm{x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{R}} \mathrm{f}_{\mathrm{n}} \left(\mathrm{x}\right)\mathrm{dx}\:\mathrm{with}\:\mathrm{f}_{\mathrm{n}} \left(\mathrm{x}\right)\:=\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{n}}\right)^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{2x}+\mathrm{1}\right) \\ $$$$\mathrm{f}_{\mathrm{n}} \:\rightarrow^{\mathrm{cs}} \:\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{2x}+\mathrm{1}\right)\:\:\mathrm{and}\:\mid\mathrm{f}_{\mathrm{n}} \mid\:\leqslant\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{integrable}\:\mathrm{on}\:\left[\mathrm{0},+\infty\left[\:\right.\right. \\ $$$$\mathrm{tbeorem}\:\mathrm{of}\:\mathrm{convegence}\:\mathrm{dominee}\:\mathrm{give}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{dx}\:=\mathrm{L} \\ $$$$\mathrm{by}\:\mathrm{parts}\:\:\mathrm{L}\:=\left[−\mathrm{e}^{−\mathrm{x}} \mathrm{ln}\left(\mathrm{2x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{+\infty} \:+\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}} \:\frac{\mathrm{2}}{\mathrm{2x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{2x}+\mathrm{1}}\mathrm{dx}\:=_{\mathrm{2x}+\mathrm{1}=\mathrm{t}} \:\:\:\mathrm{2}\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{e}^{−\left(\frac{\mathrm{t}−\mathrm{1}}{\mathrm{2}}\right)} }{\mathrm{t}}×\frac{\mathrm{dt}}{\mathrm{2}}\:=\sqrt{\mathrm{e}}\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{e}^{−\frac{\mathrm{t}}{\mathrm{2}}} }{\mathrm{t}}\mathrm{dt}…\mathrm{be}\:\mathrm{continued}… \\ $$$$ \\ $$
Answered by maths mind last updated on 28/Jun/20
![e^(−x) ≥1−x⇔,x>0 ((e^(−x) −1)/x)≥−1...true by mean valut th f(t)=e^(−t) over [0,x] x>0∃c∈[0,x] ⇒((e^(−x) −1)/x)=−e^(−c) ≥−1 ⇒e^(−(x/n)) ≥1−(x/n)⇒(1−(x/n))^n ln(1+2x)≤e^(−x) ln(1+2x) ∫_0 ^(+∞) e^(−x) ln(1+2x)dx<∞ true ⇒ convergence theorem ⇒lim_(n→∞) ∫_0 ^∞ (1−(x/n))^n ln(1+2x)dx=∫_0 ^(+∞) lim_(n→∞) (1−(x/n))^n ln(1+2x)dx =∫_0 ^(+∞) e^(−x) ln(1+2x)dx [−e^(−x) ln(1+2x)]+∫_0 ^(+∞) (e^(−x) /(1+2x))dx =∫_0 ^(+∞) (e^(−x) /(1+2x))dx=∫_1 ^(+∞) (e^(−(((u−1)/2))) /(2u))du =((√e)/2)∫_1 ^(+∞) (e^(−(u/2)) /(2u))du=((√e)/2)∫_(1/2) ^(+∞) (e^(−t) /(2t)) =((√e)/4)∫_(1/2) ^(+∞) (e^(−t) /t)dt=((√e)/4)E((1/2))](https://www.tinkutara.com/question/Q100790.png)
$${e}^{−{x}} \geqslant\mathrm{1}−{x}\Leftrightarrow,{x}>\mathrm{0} \\ $$$$\frac{{e}^{−{x}} −\mathrm{1}}{{x}}\geqslant−\mathrm{1}…{true}\:{by}\:{mean}\:{valut}\:{th} \\ $$$${f}\left({t}\right)={e}^{−{t}} \:{over}\:\left[\mathrm{0},{x}\right]\:\:{x}>\mathrm{0}\exists{c}\in\left[\mathrm{0},{x}\right] \\ $$$$\Rightarrow\frac{{e}^{−{x}} −\mathrm{1}}{{x}}=−{e}^{−{c}} \geqslant−\mathrm{1} \\ $$$$\Rightarrow{e}^{−\frac{{x}}{{n}}} \geqslant\mathrm{1}−\frac{{x}}{{n}}\Rightarrow\left(\mathrm{1}−\frac{{x}}{{n}}\right)^{{n}} {ln}\left(\mathrm{1}+\mathrm{2}{x}\right)\leqslant{e}^{−{x}} {ln}\left(\mathrm{1}+\mathrm{2}{x}\right) \\ $$$$\int_{\mathrm{0}} ^{+\infty} {e}^{−{x}} {ln}\left(\mathrm{1}+\mathrm{2}{x}\right){dx}<\infty\:\:{true} \\ $$$$\Rightarrow\:{convergence}\:{theorem} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {\mathrm{lim}}\int_{\mathrm{0}} ^{\infty} \left(\mathrm{1}−\frac{{x}}{{n}}\right)^{{n}} {ln}\left(\mathrm{1}+\mathrm{2}{x}\right){dx}=\int_{\mathrm{0}} ^{+\infty} \underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}−\frac{{x}}{{n}}\right)^{{n}} {ln}\left(\mathrm{1}+\mathrm{2}{x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} {e}^{−{x}} {ln}\left(\mathrm{1}+\mathrm{2}{x}\right){dx} \\ $$$$\left[−{e}^{−{x}} {ln}\left(\mathrm{1}+\mathrm{2}{x}\right)\right]+\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{x}} }{\mathrm{1}+\mathrm{2}{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{x}} }{\mathrm{1}+\mathrm{2}{x}}{dx}=\int_{\mathrm{1}} ^{+\infty} \frac{{e}^{−\left(\frac{{u}−\mathrm{1}}{\mathrm{2}}\right)} }{\mathrm{2}{u}}{du} \\ $$$$=\frac{\sqrt{{e}}}{\mathrm{2}}\int_{\mathrm{1}} ^{+\infty} \frac{{e}^{−\frac{{u}}{\mathrm{2}}} }{\mathrm{2}{u}}{du}=\frac{\sqrt{{e}}}{\mathrm{2}}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{+\infty} \frac{{e}^{−{t}} }{\mathrm{2}{t}} \\ $$$$=\frac{\sqrt{{e}}}{\mathrm{4}}\int_{\frac{\mathrm{1}}{\mathrm{2}}} ^{+\infty} \frac{{e}^{−{t}} }{{t}}{dt}=\frac{\sqrt{{e}}}{\mathrm{4}}{E}\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$ \\ $$
