calculation-n-1-2n-4-n-1-2-n-1-1-2-2n-k-1-1-k-2n-n-1-k-1-1-2k-2n-k-1-n-1-1-2k

Question Number 180236 by mnjuly1970 last updated on 09/Nov/22

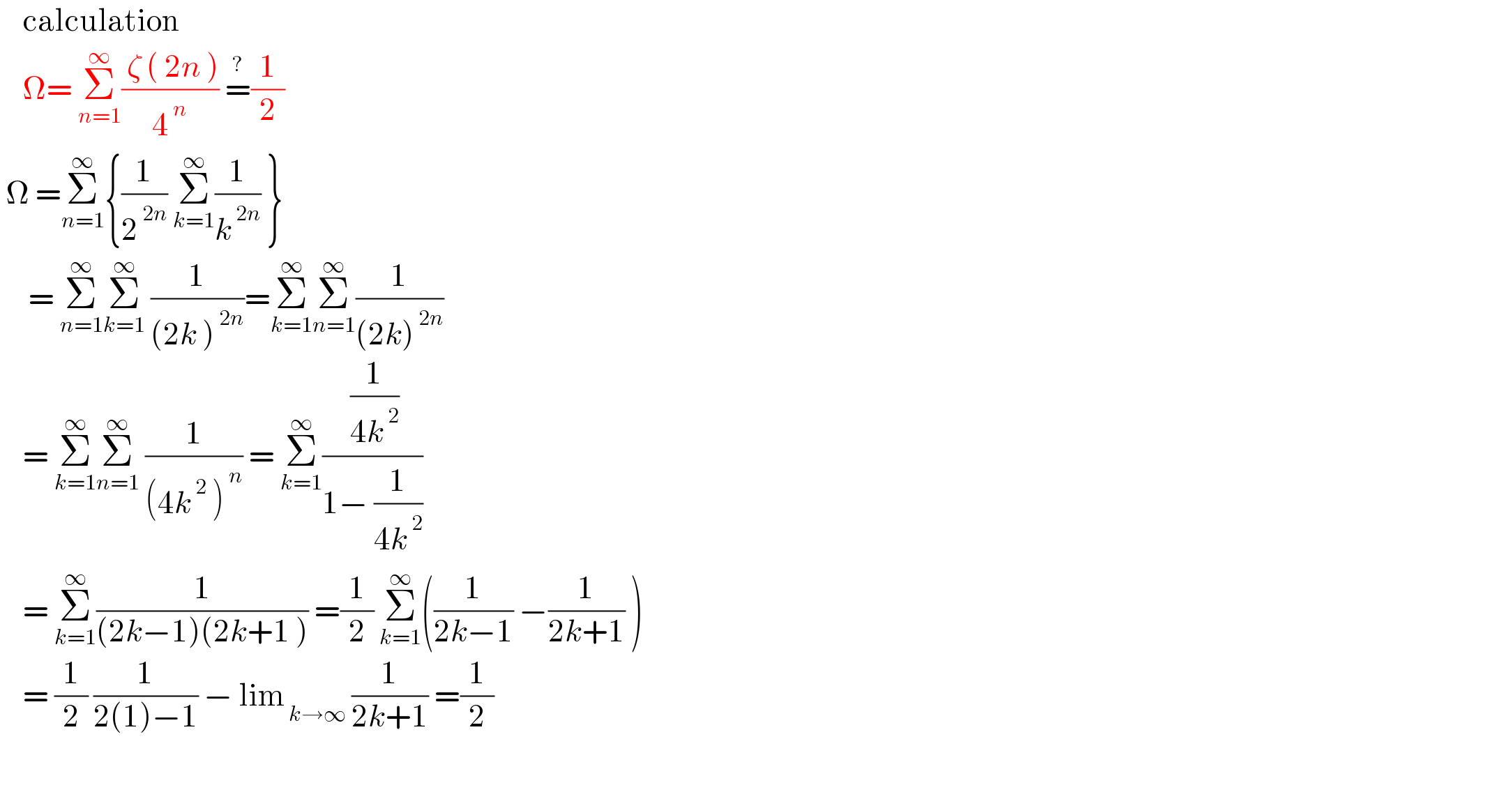
$$\:\:\:\:\mathrm{calculation} \\ $$$$\:\:\:\:\Omega=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\zeta\:\left(\:\mathrm{2}{n}\:\right)}{\mathrm{4}^{\:{n}} }\:\overset{?} {=}\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$$\:\Omega\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left\{\frac{\mathrm{1}}{\mathrm{2}^{\:\mathrm{2}{n}} }\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\:\mathrm{2}{n}} }\:\right\} \\ $$$$\:\:\:\:\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}\:\right)^{\:\mathrm{2}{n}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}\right)^{\:\mathrm{2}{n}} } \\ $$$$\:\:\:\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{4}{k}^{\:\mathrm{2}} \:\right)^{\:{n}} }\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\frac{\mathrm{1}}{\mathrm{4}{k}^{\:\mathrm{2}} }}{\mathrm{1}−\:\frac{\mathrm{1}}{\mathrm{4}{k}^{\:\mathrm{2}} }} \\ $$$$\:\:\:\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{1}\:\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:\right) \\ $$$$\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}\right)−\mathrm{1}}\:−\:\mathrm{lim}_{\:{k}\rightarrow\infty} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com