Question Number 166291 by SANOGO last updated on 17/Feb/22
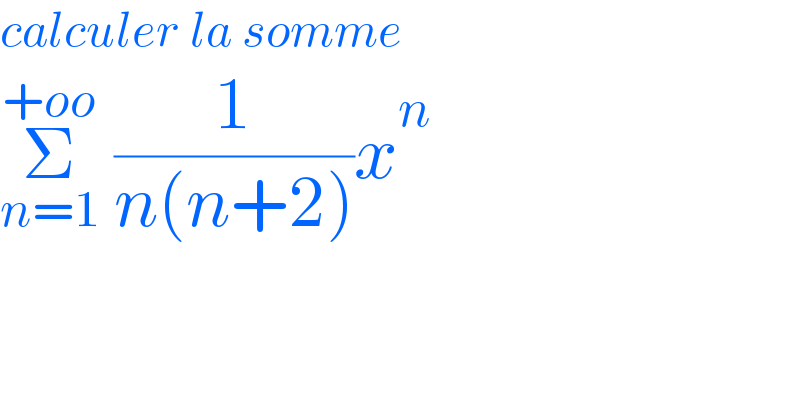
$${calculer}\:{la}\:{somme} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{+{oo}} {\sum}}\:\frac{\mathrm{1}}{{n}\left({n}+\mathrm{2}\right)}{x}^{{n}} \\ $$
Answered by TheSupreme last updated on 18/Feb/22
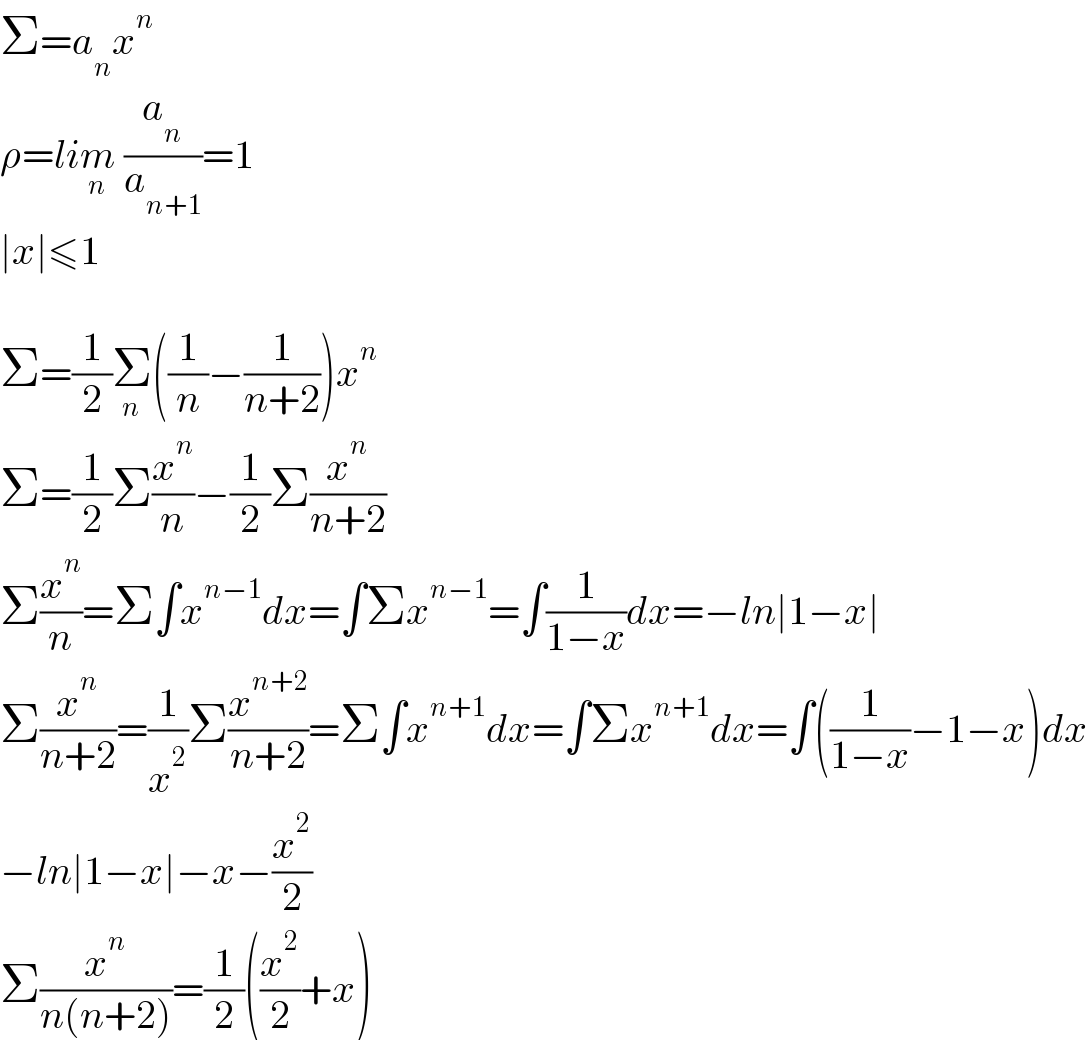
$$\Sigma={a}_{{n}} {x}^{{n}} \\ $$$$\rho={li}\underset{{n}} {{m}}\:\frac{{a}_{{n}} }{{a}_{{n}+\mathrm{1}} }=\mathrm{1} \\ $$$$\mid{x}\mid\leqslant\mathrm{1} \\ $$$$ \\ $$$$\Sigma=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}} {\sum}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right){x}^{{n}} \\ $$$$\Sigma=\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{{x}^{{n}} }{{n}}−\frac{\mathrm{1}}{\mathrm{2}}\Sigma\frac{{x}^{{n}} }{{n}+\mathrm{2}} \\ $$$$\Sigma\frac{{x}^{{n}} }{{n}}=\Sigma\int{x}^{{n}−\mathrm{1}} {dx}=\int\Sigma{x}^{{n}−\mathrm{1}} =\int\frac{\mathrm{1}}{\mathrm{1}−{x}}{dx}=−{ln}\mid\mathrm{1}−{x}\mid \\ $$$$\Sigma\frac{{x}^{{n}} }{{n}+\mathrm{2}}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\Sigma\frac{{x}^{{n}+\mathrm{2}} }{{n}+\mathrm{2}}=\Sigma\int{x}^{{n}+\mathrm{1}} {dx}=\int\Sigma{x}^{{n}+\mathrm{1}} {dx}=\int\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}−\mathrm{1}−{x}\right){dx} \\ $$$$−{ln}\mid\mathrm{1}−{x}\mid−{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Sigma\frac{{x}^{{n}} }{{n}\left({n}+\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{x}\right) \\ $$
Commented by SANOGO last updated on 18/Feb/22
$${merci}\:{bien} \\ $$
