Question Number 163316 by SANOGO last updated on 06/Jan/22

$${calculer}\:{une}\:{primitive}\:{de}\:{x}:\rightarrow{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$${puis}\:{jusrifier}\:{la}\:{convergence}\:{de}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$
Answered by amin96 last updated on 06/Jan/22
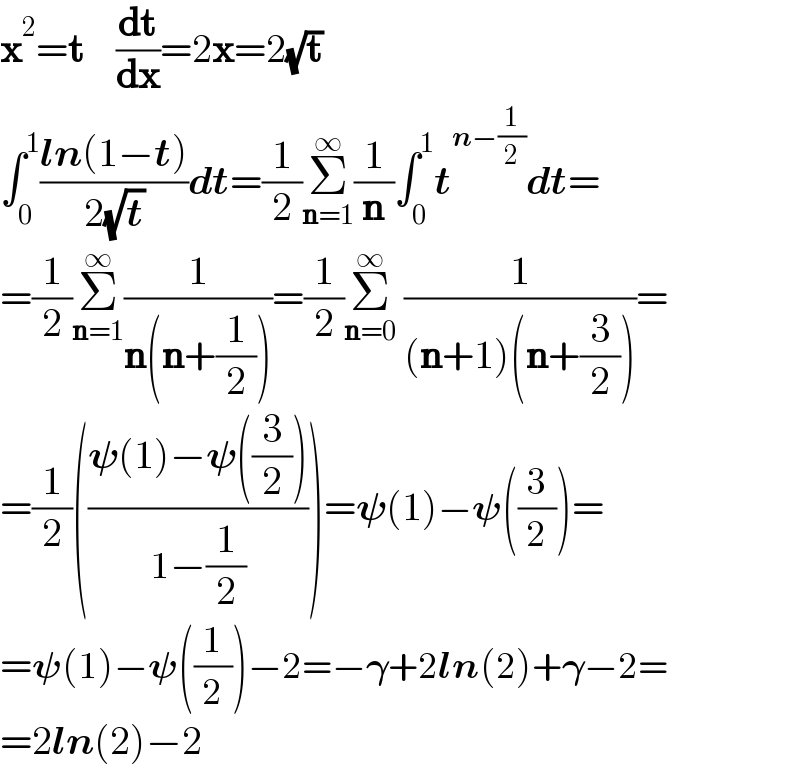
$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} =\boldsymbol{\mathrm{t}}\:\:\:\:\frac{\boldsymbol{\mathrm{dt}}}{\boldsymbol{\mathrm{dx}}}=\mathrm{2}\boldsymbol{\mathrm{x}}=\mathrm{2}\sqrt{\boldsymbol{\mathrm{t}}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{ln}}\left(\mathrm{1}−\boldsymbol{{t}}\right)}{\mathrm{2}\sqrt{\boldsymbol{{t}}}}\boldsymbol{{dt}}=\frac{\mathrm{1}}{\mathrm{2}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}}\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{{t}}^{\boldsymbol{{n}}−\frac{\mathrm{1}}{\mathrm{2}}} \boldsymbol{{dt}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{n}}+\frac{\mathrm{3}}{\mathrm{2}}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\boldsymbol{\psi}\left(\mathrm{1}\right)−\boldsymbol{\psi}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}\right)=\boldsymbol{\psi}\left(\mathrm{1}\right)−\boldsymbol{\psi}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)= \\ $$$$=\boldsymbol{\psi}\left(\mathrm{1}\right)−\boldsymbol{\psi}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}=−\boldsymbol{\gamma}+\mathrm{2}\boldsymbol{{ln}}\left(\mathrm{2}\right)+\boldsymbol{\gamma}−\mathrm{2}= \\ $$$$=\mathrm{2}\boldsymbol{{ln}}\left(\mathrm{2}\right)−\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 06/Jan/22

$$\mathrm{2}{ln}\left(\mathrm{2}\right)−\mathrm{2} \\ $$
Commented by amin96 last updated on 06/Jan/22
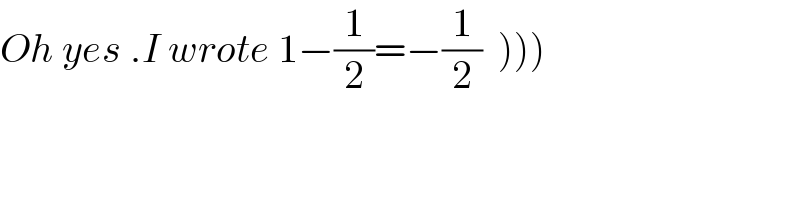
$$\left.{O}\left.{h}\left.\:{yes}\:.{I}\:{wrote}\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{1}}{\mathrm{2}}\:\:\right)\right)\right) \\ $$
Answered by smallEinstein last updated on 06/Jan/22

Answered by mnjuly1970 last updated on 06/Jan/22
![Ω= ∫_0 ^( 1) ln(x)dx + ∫_1 ^( 2) ln(x)dx = ∫_0 ^( 2) ln(x)dx=[xln(x)−x]_0 ^2 2ln(2)−2 =ln(4)−2](https://www.tinkutara.com/question/Q163351.png)
$$\:\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left({x}\right){dx}\:+\:\int_{\mathrm{1}} ^{\:\mathrm{2}} {ln}\left({x}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\int_{\mathrm{0}} ^{\:\mathrm{2}} {ln}\left({x}\right){dx}=\left[{xln}\left({x}\right)−{x}\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{2}{ln}\left(\mathrm{2}\right)−\mathrm{2}\:={ln}\left(\mathrm{4}\right)−\mathrm{2} \\ $$
