Question Number 90044 by abdomathmax last updated on 21/Apr/20
![calculste ∫_0 ^1 sin([2x] −[(1/x)])dx](https://www.tinkutara.com/question/Q90044.png)
$${calculste}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{sin}\left(\left[\mathrm{2}{x}\right]\:−\left[\frac{\mathrm{1}}{{x}}\right]\right){dx} \\ $$
Commented by mathmax by abdo last updated on 24/Apr/20
![I =∫_0 ^1 sin([2x]−[(1/x)])dx ⇒I=_(x=(1/t)) ∫_1 ^∞ sin([(2/t)]−[t])(dt/t^2 ) =∫_1 ^2 sin([(2/t)]−[t])(dt/t^2 ) +∫_2 ^(+∞) (1/t^2 ) sin([(2/t)]−[t])dt 1≤t<2 ⇒(1/2)<(1/t)<1 ⇒1<(2/t)<2 ⇒[(2/t)]=1 also[t]=1 ⇒ ∫_1 ^2 sin([(2/t)]−[t])(dt/t^2 )=0 ⇒ I =∫_2 ^(+∞) (1/t^2 )sin([(2/t)]−[t])dt t>2 ⇒0<(1/t)<(1/2) ⇒0<(2/t)<1 ⇒[(2/t)]=0 ⇒I =−∫_2 ^(+∞) ((sin[t])/t^2 )dt =−Σ_(k=2) ^∞ ∫_k ^(k+1) ((sink)/t^2 )dt =−Σ_(k=2) ^∞ sink[−(1/t)]_k ^(k+1) =Σ_(k=2) ^∞ sink((1/(k+1))−(1/k)) =Σ_(k=2) ^∞ ((sink)/(k+1))−Σ_(k=2) ^∞ ((sink)/k) Σ_(k=2) ^∞ ((sink)/k) =Im(Σ_(k=1) ^∞ (e^(ik) /k))−sin(1) let w(z)=Σ_(k=1) ^∞ (z^k /k) ⇒w^′ (x) =Σ_(k=1) ^∞ z^(k−1) =Σ_(k=0) ^∞ z^k =(1/(1−z)) (∣z∣<1) w(z) =∫_0 ^z (dt/(1−t)) +k k=w(0) =0 ⇒w(z)=−ln(1−z) Σ_(k=1) ^∞ (e^(ik) /k) =−ln(1−e^i ) =−ln(1−cos(1)−isin(1)) =−ln(2sin^2 ((1/2))−2isin((1/2))cos((1/2))) =−ln(−isin((1/2))e^(i/2) ) =−ln(−i)−ln(sin((1/2)))−(i/2) =−ln(e^(−((iπ)/2)) )−(i/2)−ln(sin((1/2))) =((iπ)/2)−(i/2) ⇒Σ_(k=2) ^∞ ((sink)/k) =((π−1)/2) −sin(1) we follow the same for Σ_(k=2) ^∞ ((sink)/(k+1))...](https://www.tinkutara.com/question/Q90493.png)
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:{sin}\left(\left[\mathrm{2}{x}\right]−\left[\frac{\mathrm{1}}{{x}}\right]\right){dx}\:\Rightarrow{I}=_{{x}=\frac{\mathrm{1}}{{t}}} \:\:\int_{\mathrm{1}} ^{\infty} \:{sin}\left(\left[\frac{\mathrm{2}}{{t}}\right]−\left[{t}\right]\right)\frac{{dt}}{{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \:{sin}\left(\left[\frac{\mathrm{2}}{{t}}\right]−\left[{t}\right]\right)\frac{{dt}}{{t}^{\mathrm{2}} }\:+\int_{\mathrm{2}} ^{+\infty} \frac{\mathrm{1}}{{t}^{\mathrm{2}} }\:{sin}\left(\left[\frac{\mathrm{2}}{{t}}\right]−\left[{t}\right]\right){dt} \\ $$$$\mathrm{1}\leqslant{t}<\mathrm{2}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}<\frac{\mathrm{1}}{{t}}<\mathrm{1}\:\Rightarrow\mathrm{1}<\frac{\mathrm{2}}{{t}}<\mathrm{2}\:\Rightarrow\left[\frac{\mathrm{2}}{{t}}\right]=\mathrm{1}\:{also}\left[{t}\right]=\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \:{sin}\left(\left[\frac{\mathrm{2}}{{t}}\right]−\left[{t}\right]\right)\frac{{dt}}{{t}^{\mathrm{2}} }=\mathrm{0}\:\Rightarrow\:{I}\:=\int_{\mathrm{2}} ^{+\infty} \:\frac{\mathrm{1}}{{t}^{\mathrm{2}} }{sin}\left(\left[\frac{\mathrm{2}}{{t}}\right]−\left[{t}\right]\right){dt} \\ $$$${t}>\mathrm{2}\:\Rightarrow\mathrm{0}<\frac{\mathrm{1}}{{t}}<\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{0}<\frac{\mathrm{2}}{{t}}<\mathrm{1}\:\Rightarrow\left[\frac{\mathrm{2}}{{t}}\right]=\mathrm{0}\:\Rightarrow{I}\:=−\int_{\mathrm{2}} ^{+\infty} \:\frac{{sin}\left[{t}\right]}{{t}^{\mathrm{2}} }{dt} \\ $$$$=−\sum_{{k}=\mathrm{2}} ^{\infty} \:\int_{{k}} ^{{k}+\mathrm{1}} \:\frac{{sink}}{{t}^{\mathrm{2}} }{dt}\:=−\sum_{{k}=\mathrm{2}} ^{\infty} \:{sink}\left[−\frac{\mathrm{1}}{{t}}\right]_{{k}} ^{{k}+\mathrm{1}} \\ $$$$=\sum_{{k}=\mathrm{2}} ^{\infty} \:{sink}\left(\frac{\mathrm{1}}{{k}+\mathrm{1}}−\frac{\mathrm{1}}{{k}}\right)\:=\sum_{{k}=\mathrm{2}} ^{\infty} \:\frac{{sink}}{{k}+\mathrm{1}}−\sum_{{k}=\mathrm{2}} ^{\infty} \:\frac{{sink}}{{k}} \\ $$$$\sum_{{k}=\mathrm{2}} ^{\infty} \:\frac{{sink}}{{k}}\:={Im}\left(\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{{e}^{{ik}} }{{k}}\right)−{sin}\left(\mathrm{1}\right) \\ $$$${let}\:{w}\left({z}\right)=\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{{z}^{{k}} }{{k}}\:\Rightarrow{w}^{'} \left({x}\right)\:=\sum_{{k}=\mathrm{1}} ^{\infty} \:{z}^{{k}−\mathrm{1}} \:=\sum_{{k}=\mathrm{0}} ^{\infty} \:{z}^{{k}} \:=\frac{\mathrm{1}}{\mathrm{1}−{z}}\:\:\left(\mid{z}\mid<\mathrm{1}\right) \\ $$$${w}\left({z}\right)\:=\int_{\mathrm{0}} ^{{z}} \:\frac{{dt}}{\mathrm{1}−{t}}\:+{k}\:\:{k}={w}\left(\mathrm{0}\right)\:=\mathrm{0}\:\Rightarrow{w}\left({z}\right)=−{ln}\left(\mathrm{1}−{z}\right) \\ $$$$\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{{e}^{{ik}} }{{k}}\:=−{ln}\left(\mathrm{1}−{e}^{{i}} \right)\:=−{ln}\left(\mathrm{1}−{cos}\left(\mathrm{1}\right)−{isin}\left(\mathrm{1}\right)\right) \\ $$$$=−{ln}\left(\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}{isin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$=−{ln}\left(−{isin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){e}^{\frac{{i}}{\mathrm{2}}} \right)\:=−{ln}\left(−{i}\right)−{ln}\left({sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)−\frac{{i}}{\mathrm{2}} \\ $$$$=−{ln}\left({e}^{−\frac{{i}\pi}{\mathrm{2}}} \right)−\frac{{i}}{\mathrm{2}}−{ln}\left({sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$=\frac{{i}\pi}{\mathrm{2}}−\frac{{i}}{\mathrm{2}}\:\Rightarrow\sum_{{k}=\mathrm{2}} ^{\infty} \:\frac{{sink}}{{k}}\:=\frac{\pi−\mathrm{1}}{\mathrm{2}}\:−{sin}\left(\mathrm{1}\right)\:{we}\:{follow}\:{the}\:{same}\:{for} \\ $$$$\sum_{{k}=\mathrm{2}} ^{\infty} \:\frac{{sink}}{{k}+\mathrm{1}}… \\ $$
Commented by mathmax by abdo last updated on 24/Apr/20
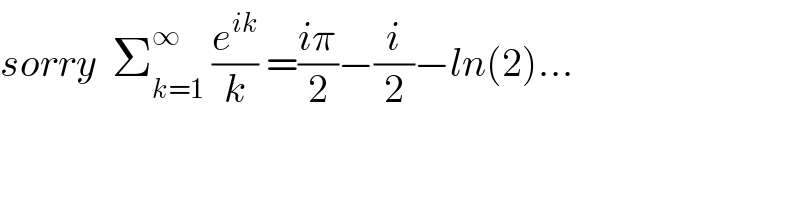
$${sorry}\:\:\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{{e}^{{ik}} }{{k}}\:=\frac{{i}\pi}{\mathrm{2}}−\frac{{i}}{\mathrm{2}}−{ln}\left(\mathrm{2}\right)… \\ $$
