calculste-0-ln-x-1-x-4-dx-

Question Number 108749 by mathmax by abdo last updated on 19/Aug/20

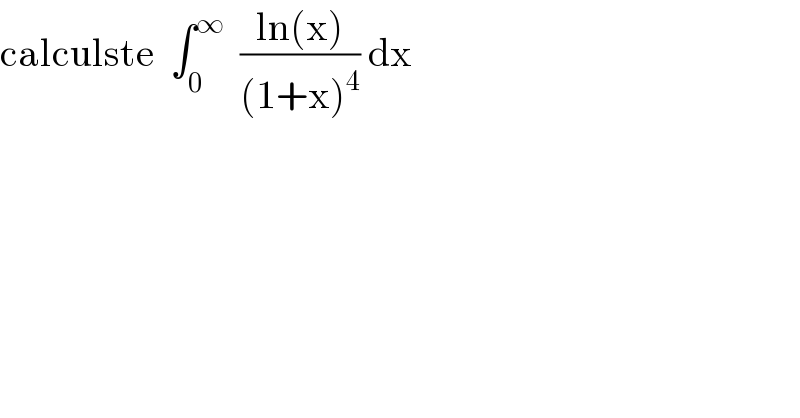
$$\mathrm{calculste}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{4}} }\:\mathrm{dx} \\ $$

Answered by mnjuly1970 last updated on 19/Aug/20

f(a)=∫_0 ^( ∞) (x^a /((1+x)^4 ))⇒goal:=f^( ′) (0) f^( ′) (a)=(d/da)[β(a+1,3−a)]=(1/6)(d/da)[Γ(a+1).Γ(3−a)] =(1/6) [Γ^( ′) (1).Γ(3)−Γ^( ′) (3)Γ(1)] =(1/6)[−2γ−2ψ(3)]=(1/6)[−2γ−2((3/2) − γ)] ((−1)/2) ....

$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{{a}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{4}} }\Rightarrow\mathrm{goal}:={f}^{\:'} \left(\mathrm{0}\right) \\ $$$${f}^{\:'} \left({a}\right)=\frac{{d}}{{da}}\left[\beta\left({a}+\mathrm{1},\mathrm{3}−{a}\right)\right]=\frac{\mathrm{1}}{\mathrm{6}}\frac{{d}}{{da}}\left[\Gamma\left({a}+\mathrm{1}\right).\Gamma\left(\mathrm{3}−{a}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{6}}\:\left[\Gamma^{\:'} \left(\mathrm{1}\right).\Gamma\left(\mathrm{3}\right)−\Gamma^{\:'} \left(\mathrm{3}\right)\Gamma\left(\mathrm{1}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[−\mathrm{2}\gamma−\mathrm{2}\psi\left(\mathrm{3}\right)\right]=\frac{\mathrm{1}}{\mathrm{6}}\left[−\mathrm{2}\gamma−\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{2}}\:−\:\gamma\right)\right] \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}\:…. \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 19/Aug/20

$$\mathrm{thankx}\:\mathrm{sir} \\ $$

Commented by mnjuly1970 last updated on 19/Aug/20

$${thank}\:{you}\:{master}..{yourquestions} \\ $$$${are}\:{very}\:{nice}… \\ $$

Answered by mathmax by abdo last updated on 19/Aug/20

we use ∫_0 ^∞ q(x)ln(x) =−(1/2)Re(Σ_i Re(q(z)ln^2 z ,a_i ) we have q(z)ln^2 z =((ln^2 z)/((z+1)^4 ))=w(z) ⇒−1 is pole of (with ordr 4) Res(w,−1) =lim_(z→−1) (1/((4−1)!)){(z+1)^4 w(z)}^((3)) =(1/6)lim_(z→−1) {ln^2 (z)}^((3)) =(1/6)lim_(z→−1) {((2lnz)/z)}^((2)) =(1/3)lim_(z→−1) {((1−lnz)/z^2 )}^((1)) =(1/3)lim_(z→−1) {((−z−2z(1−lnz))/z^4 )} =(1/3)lim_(z→−1) {((−1−2(1−lnz))/z^3 )} =(1/3)lim_(z→−1) {((−3+2ln(z))/z^3 )} =(1/3).(3−2ln(−1)) =1−(2/3)ln(e^(iπ) ) =1−((2iπ)/3) ⇒Re(...)=1 ⇒ ∫_0 ^∞ ((lnx)/((1+x)^4 ))dx =−(1/2)

$$\mathrm{we}\:\mathrm{use}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{q}\left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{x}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\sum_{\mathrm{i}} \mathrm{Re}\left(\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z}\:,\mathrm{a}_{\mathrm{i}} \right)\:\:\right. \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z}\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{4}} }=\mathrm{w}\left(\mathrm{z}\right)\:\Rightarrow−\mathrm{1}\:\mathrm{is}\:\mathrm{pole}\:\mathrm{of}\:\left(\mathrm{with}\:\mathrm{ordr}\:\mathrm{4}\right) \\ $$$$\mathrm{Res}\left(\mathrm{w},−\mathrm{1}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \:\frac{\mathrm{1}}{\left(\mathrm{4}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{4}} \mathrm{w}\left(\mathrm{z}\right)\right\}^{\left(\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \left\{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{z}\right)\right\}^{\left(\mathrm{3}\right)} \:=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \left\{\frac{\mathrm{2lnz}}{\mathrm{z}}\right\}^{\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \:\left\{\frac{\mathrm{1}−\mathrm{lnz}}{\mathrm{z}^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \left\{\frac{−\mathrm{z}−\mathrm{2z}\left(\mathrm{1}−\mathrm{lnz}\right)}{\mathrm{z}^{\mathrm{4}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \left\{\frac{−\mathrm{1}−\mathrm{2}\left(\mathrm{1}−\mathrm{lnz}\right)}{\mathrm{z}^{\mathrm{3}} }\right\}\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{lim}_{\mathrm{z}\rightarrow−\mathrm{1}} \:\:\left\{\frac{−\mathrm{3}+\mathrm{2ln}\left(\mathrm{z}\right)}{\mathrm{z}^{\mathrm{3}} }\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}.\left(\mathrm{3}−\mathrm{2ln}\left(−\mathrm{1}\right)\right)\:=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{ln}\left(\mathrm{e}^{\mathrm{i}\pi} \right)\:=\mathrm{1}−\frac{\mathrm{2i}\pi}{\mathrm{3}}\:\Rightarrow\mathrm{Re}\left(…\right)=\mathrm{1}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{lnx}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{4}} }\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$

Facebook Tweet Pin

calculste-0-ln-x-1-x-4-dx-

Leave a Reply Cancel reply