Question Number 108750 by mathmax by abdo last updated on 19/Aug/20
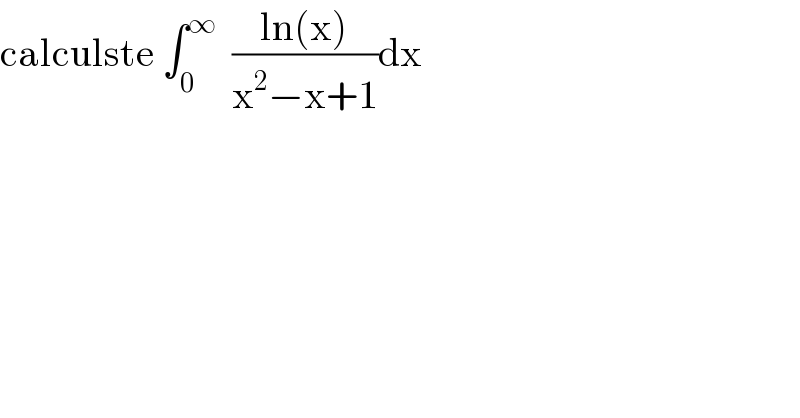
$$\mathrm{calculste}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$
Answered by mnjuly1970 last updated on 19/Aug/20
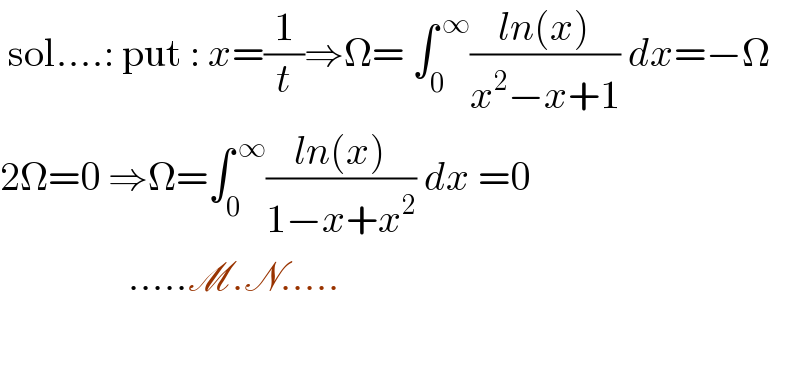
$$\:\mathrm{sol}….:\:\mathrm{put}\::\:{x}=\frac{\mathrm{1}}{{t}}\Rightarrow\Omega=\:\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:{dx}=−\Omega \\ $$$$\mathrm{2}\Omega=\mathrm{0}\:\Rightarrow\Omega=\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({x}\right)}{\mathrm{1}−{x}+{x}^{\mathrm{2}} }\:{dx}\:=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\mathscr{M}.\mathscr{N}….. \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 19/Aug/20

$$\mathrm{if}\:\mathrm{q}\:\mathrm{is}\:\mathrm{a}\:\mathrm{fraction}\:\mathrm{with}\:\mathrm{no}\:\mathrm{real}\:\mathrm{poles}\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \mathrm{q}\left(\mathrm{x}\right)\mathrm{lnx}\:\mathrm{dx}\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{Re}\left(\sum_{\mathrm{i}} \:\mathrm{Re}\left(\:\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z},\mathrm{a}_{\mathrm{i}} \right)\:\mathrm{let}\:\mathrm{use}\:\mathrm{this}\right. \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \mathrm{z}\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}}\:=\mathrm{w}\left(\mathrm{z}\right)\:\mathrm{poles}? \\ $$$$\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\mathrm{1}\:=\mathrm{0}\:\rightarrow\Delta\:=−\mathrm{3}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \\ $$$$\mathrm{w}\left(\mathrm{z}\right)\:=\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{z}}{\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)}\:\Rightarrow\mathrm{Res}\left(\mathrm{w},\mathrm{z}_{\mathrm{1}} \right)\:=\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{z}_{\mathrm{1}} \right)}{\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} }\:=\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)}{\mathrm{i}\sqrt{\mathrm{3}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{i}\sqrt{\mathrm{3}}}\left(\frac{\mathrm{i2}\pi}{\mathrm{3}}\right)^{\mathrm{2}} \:=\frac{−\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{3i}\sqrt{\mathrm{3}}}\:\:\mathrm{also}\:\mathrm{Res}\left(\mathrm{w},\mathrm{z}_{\mathrm{2}} \right)\:=\frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{z}_{\mathrm{2}} \right)}{\mathrm{z}_{\mathrm{2}} −\mathrm{z}_{\mathrm{1}} }\:=\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{3i}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\Sigma\:\mathrm{Re}\left(\mathrm{q}\left(\mathrm{z}\right)\mathrm{ln}^{\mathrm{2}} \left(\mathrm{z}\right),\mathrm{a}_{\mathrm{i}} \right)=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\mathrm{dx}\:=\mathrm{0} \\ $$$$ \\ $$
