Menu Close

calculste-0-xarctan-2x-9-2x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 90041 by abdomathmax last updated on 21/Apr/20
calculste ∫_0 ^∞ ((xarctan(2x))/(9+2x^2 ))dx
$${calculste}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xarctan}\left(\mathrm{2}{x}\right)}{\mathrm{9}+\mathrm{2}{x}^{\mathrm{2}} }{dx}\: \\ $$
Answered by mathmax by abdo last updated on 23/Apr/20
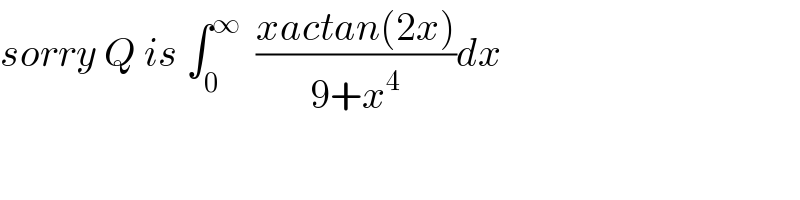
sorry Q is ∫_0 ^∞ ((xactan(2x))/(9+x^4 ))dx
$${sorry}\:{Q}\:{is}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xactan}\left(\mathrm{2}{x}\right)}{\mathrm{9}+{x}^{\mathrm{4}} }{dx} \\ $$
Commented by mathmax by abdo last updated on 24/Apr/20
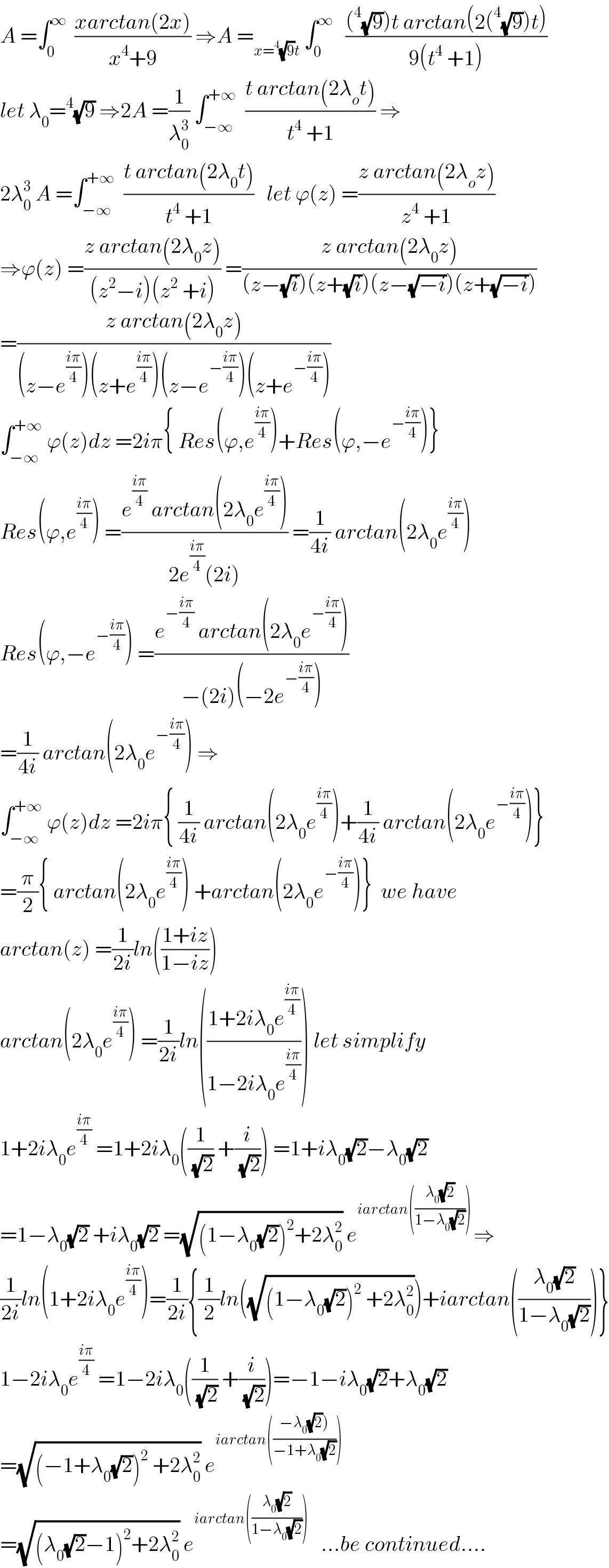
A =∫_0 ^∞ ((xarctan(2x))/(x^4 +9)) ⇒A =_(x=^4 (√9)t) ∫_0 ^∞ (((^4 (√9))t arctan(2(^4 (√9))t))/(9(t^4 +1))) let λ_0 =^4 (√9) ⇒2A =(1/λ_0 ^3 ) ∫_(−∞) ^(+∞) ((t arctan(2λ_o t))/(t^4 +1)) ⇒ 2λ_0 ^3 A =∫_(−∞) ^(+∞) ((t arctan(2λ_0 t))/(t^4 +1)) let ϕ(z) =((z arctan(2λ_o z))/(z^4 +1)) ⇒ϕ(z) =((z arctan(2λ_0 z))/((z^2 −i)(z^2 +i))) =((z arctan(2λ_0 z))/((z−(√i))(z+(√i))(z−(√(−i)))(z+(√(−i))))) =((z arctan(2λ_0 z))/((z−e^((iπ)/4) )(z+e^((iπ)/4) )(z−e^(−((iπ)/4)) )(z+e^(−((iπ)/4)) ))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,e^((iπ)/4) )+Res(ϕ,−e^(−((iπ)/4)) )} Res(ϕ,e^((iπ)/4) ) =((e^((iπ)/4) arctan(2λ_0 e^((iπ)/4) ))/(2e^((iπ)/4) (2i))) =(1/(4i)) arctan(2λ_0 e^((iπ)/4) ) Res(ϕ,−e^(−((iπ)/4)) ) =((e^(−((iπ)/4)) arctan(2λ_0 e^(−((iπ)/4)) ))/(−(2i)(−2e^(−((iπ)/4)) ))) =(1/(4i)) arctan(2λ_0 e^(−((iπ)/4)) ) ⇒ ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ (1/(4i)) arctan(2λ_0 e^((iπ)/4) )+(1/(4i)) arctan(2λ_0 e^(−((iπ)/4)) )} =(π/2){ arctan(2λ_0 e^((iπ)/4) ) +arctan(2λ_0 e^(−((iπ)/4)) )} we have arctan(z) =(1/(2i))ln(((1+iz)/(1−iz))) arctan(2λ_0 e^((iπ)/4) ) =(1/(2i))ln(((1+2iλ_0 e^((iπ)/4) )/(1−2iλ_0 e^((iπ)/4) ))) let simplify 1+2iλ_0 e^((iπ)/4) =1+2iλ_0 ((1/( (√2))) +(i/( (√2)))) =1+iλ_0 (√2)−λ_0 (√2) =1−λ_0 (√2) +iλ_0 (√2) =(√((1−λ_0 (√2))^2 +2λ_0 ^2 )) e^(iarctan(((λ_0 (√2))/(1−λ_0 (√2)))) ) ⇒ (1/(2i))ln(1+2iλ_0 e^((iπ)/4) )=(1/(2i)){(1/2)ln((√((1−λ_0 (√2))^2 +2λ_0 ^2 )))+iarctan(((λ_0 (√2))/(1−λ_0 (√2))))} 1−2iλ_0 e^((iπ)/4) =1−2iλ_0 ((1/( (√2))) +(i/( (√2))))=−1−iλ_0 (√2)+λ_0 (√2) =(√((−1+λ_0 (√2))^2 +2λ_0 ^2 )) e^(iarctan(((−λ_0 (√2)))/(−1+λ_0 (√2))))) =(√((λ_0 (√2)−1)^2 +2λ_0 ^2 )) e^(iarctan(((λ_0 (√2))/(1−λ_0 (√2))))) ...be continued....
$${A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{xarctan}\left(\mathrm{2}{x}\right)}{{x}^{\mathrm{4}} +\mathrm{9}}\:\Rightarrow{A}\:=_{{x}=^{\mathrm{4}} \sqrt{\mathrm{9}}{t}} \:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\left(^{\mathrm{4}} \sqrt{\mathrm{9}}\right){t}\:{arctan}\left(\mathrm{2}\left(^{\mathrm{4}} \sqrt{\mathrm{9}}\right){t}\right)}{\mathrm{9}\left({t}^{\mathrm{4}} \:+\mathrm{1}\right)} \\ $$$${let}\:\lambda_{\mathrm{0}} =^{\mathrm{4}} \sqrt{\mathrm{9}}\:\Rightarrow\mathrm{2}{A}\:=\frac{\mathrm{1}}{\lambda_{\mathrm{0}} ^{\mathrm{3}} }\:\int_{−\infty} ^{+\infty} \:\:\frac{{t}\:{arctan}\left(\mathrm{2}\lambda_{{o}} {t}\right)}{{t}^{\mathrm{4}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{2}\lambda_{\mathrm{0}} ^{\mathrm{3}} \:{A}\:=\int_{−\infty} ^{+\infty} \:\:\frac{{t}\:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {t}\right)}{{t}^{\mathrm{4}} \:+\mathrm{1}}\:\:\:{let}\:\varphi\left({z}\right)\:=\frac{{z}\:{arctan}\left(\mathrm{2}\lambda_{{o}} {z}\right)}{{z}^{\mathrm{4}} \:+\mathrm{1}} \\ $$$$\Rightarrow\varphi\left({z}\right)\:=\frac{{z}\:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {z}\right)}{\left({z}^{\mathrm{2}} −{i}\right)\left({z}^{\mathrm{2}} \:+{i}\right)}\:=\frac{{z}\:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {z}\right)}{\left({z}−\sqrt{{i}}\right)\left({z}+\sqrt{{i}}\right)\left({z}−\sqrt{−{i}}\right)\left({z}+\sqrt{−{i}}\right)} \\ $$$$=\frac{{z}\:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {z}\right)}{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$${Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:=\frac{{e}^{\frac{{i}\pi}{\mathrm{4}}} \:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {e}^{\frac{{i}\pi}{\mathrm{4}}} \right)}{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{4}}} \left(\mathrm{2}{i}\right)}\:=\frac{\mathrm{1}}{\mathrm{4}{i}}\:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {e}^{\frac{{i}\pi}{\mathrm{4}}} \right) \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:=\frac{{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)}{−\left(\mathrm{2}{i}\right)\left(−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{i}}\:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\frac{\mathrm{1}}{\mathrm{4}{i}}\:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {e}^{\frac{{i}\pi}{\mathrm{4}}} \right)+\frac{\mathrm{1}}{\mathrm{4}{i}}\:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\} \\ $$$$=\frac{\pi}{\mathrm{2}}\left\{\:{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:+{arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\right\}\:\:{we}\:{have} \\ $$$${arctan}\left({z}\right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+{iz}}{\mathrm{1}−{iz}}\right) \\ $$$${arctan}\left(\mathrm{2}\lambda_{\mathrm{0}} {e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\:=\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\frac{\mathrm{1}+\mathrm{2}{i}\lambda_{\mathrm{0}} {e}^{\frac{{i}\pi}{\mathrm{4}}} }{\mathrm{1}−\mathrm{2}{i}\lambda_{\mathrm{0}} {e}^{\frac{{i}\pi}{\mathrm{4}}} }\right)\:{let}\:{simplify} \\ $$$$\mathrm{1}+\mathrm{2}{i}\lambda_{\mathrm{0}} {e}^{\frac{{i}\pi}{\mathrm{4}}} \:=\mathrm{1}+\mathrm{2}{i}\lambda_{\mathrm{0}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)\:=\mathrm{1}+{i}\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}−\lambda_{\mathrm{0}} \sqrt{\mathrm{2}} \\ $$$$=\mathrm{1}−\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}\:+{i}\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}\:=\sqrt{\left(\mathrm{1}−\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\lambda_{\mathrm{0}} ^{\mathrm{2}} }\:{e}^{{iarctan}\left(\frac{\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}}{\mathrm{1}−\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}}\right)\:} \Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{i}}{ln}\left(\mathrm{1}+\mathrm{2}{i}\lambda_{\mathrm{0}} {e}^{\frac{{i}\pi}{\mathrm{4}}} \right)=\frac{\mathrm{1}}{\mathrm{2}{i}}\left\{\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\sqrt{\left(\mathrm{1}−\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:+\mathrm{2}\lambda_{\mathrm{0}} ^{\mathrm{2}} }\right)+{iarctan}\left(\frac{\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}}{\mathrm{1}−\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}}\right)\right\} \\ $$$$\mathrm{1}−\mathrm{2}{i}\lambda_{\mathrm{0}} {e}^{\frac{{i}\pi}{\mathrm{4}}} \:=\mathrm{1}−\mathrm{2}{i}\lambda_{\mathrm{0}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)=−\mathrm{1}−{i}\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}+\lambda_{\mathrm{0}} \sqrt{\mathrm{2}} \\ $$$$=\sqrt{\left(−\mathrm{1}+\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:+\mathrm{2}\lambda_{\mathrm{0}} ^{\mathrm{2}} }\:{e}^{{iarctan}\left(\frac{\left.−\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}\right)}{−\mathrm{1}+\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}}\right)} \\ $$$$=\sqrt{\left(\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}\lambda_{\mathrm{0}} ^{\mathrm{2}} }\:{e}^{{iarctan}\left(\frac{\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}}{\mathrm{1}−\lambda_{\mathrm{0}} \sqrt{\mathrm{2}}}\right)} \:\:\:…{be}\:{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *