Question Number 98424 by mathmax by abdo last updated on 13/Jun/20
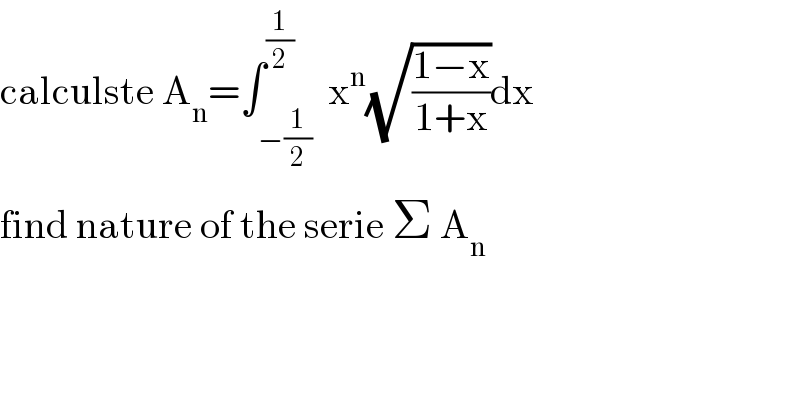
$$\mathrm{calculste}\:\mathrm{A}_{\mathrm{n}} =\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{x}^{\mathrm{n}} \sqrt{\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}}\mathrm{dx} \\ $$$$\mathrm{find}\:\mathrm{nature}\:\mathrm{of}\:\mathrm{the}\:\mathrm{serie}\:\Sigma\:\mathrm{A}_{\mathrm{n}} \\ $$
Answered by maths mind last updated on 14/Jun/20

$${x}={cos}\left(\mathrm{2}{a}\right) \\ $$$$\Rightarrow\int_{\frac{\mathrm{5}\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{6}}} {cos}^{{n}} \left(\mathrm{2}{a}\right)\sqrt{{tg}^{\mathrm{2}} \left({a}\right)}.−\mathrm{2}{sin}\left(\mathrm{2}{a}\right){da}..{A} \\ $$$$=\int−\mathrm{4}{cos}^{{n}} \left(\mathrm{2}{a}\right){tg}\left({a}\right){sin}\left({a}\right){cos}\left({a}\right){da} \\ $$$$=\int−\mathrm{4}{cos}^{{n}} \left(\mathrm{2}{a}\right){sin}^{\mathrm{2}} \left({a}\right) \\ $$$$=\mathrm{2}\int{cos}^{{n}} \left(\mathrm{2}{a}\right)\left({cos}\left(\mathrm{2}{a}\right)−\mathrm{1}\right){da} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \left\{{cos}^{{n}+\mathrm{1}} \left(\mathrm{2}{a}\right)−{cos}^{{n}} \left(\mathrm{2}{a}\right)\right\}{da} \\ $$$$=\mathrm{2}\int{cos}^{{n}+\mathrm{1}} \left(\mathrm{2}{a}\right)−\mathrm{2}\int{cos}^{{n}} \left(\mathrm{2}{a}\right){da} \\ $$$$=\int{cos}^{{n}+\mathrm{1}} \left({s}\right){ds}−\int{cos}^{{n}} \left({s}\right){ds}..{I} \\ $$$${B}\left({x};{a},{b}\right)=\int_{\mathrm{0}} ^{{x}} {t}^{{a}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{b}−\mathrm{1}} {dt}\:…{incompletd}\:{Betta}\:{function} \\ $$$$\int{cos}^{{n}} \left({t}\right){dt},\:\:\:{u}={cos}^{\mathrm{2}} \left({t}\right) \\ $$$$−\mathrm{2}\int{u}^{\frac{{n}}{\mathrm{2}}+\mathrm{1}} \left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {du}=−\mathrm{2}\beta\left({u};\frac{{n}}{\mathrm{2}}+\mathrm{2},\frac{\mathrm{3}}{\mathrm{2}}\right)+{c} \\ $$$$.−\mathrm{2}\beta\left({cos}^{\mathrm{2}} \left({t}\right);\frac{{n}}{\mathrm{2}}+\mathrm{2},\frac{\mathrm{3}}{\mathrm{2}}\right)…{I} \\ $$$$\int_{\frac{\mathrm{5}\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{{n}} \left({t}\right){dt}..{withe} \\ $$$${t}=\pi−{c} \\ $$$$\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{6}}} \left(−\mathrm{1}\right)^{{n}} {cos}^{{n}} \left({t}\right) \\ $$$${A}=−\mathrm{2}\int_{\frac{\mathrm{5}\pi\:}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{{n}+\mathrm{1}} \left({t}\right)+\mathrm{2}\int_{\frac{\mathrm{5}\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{{n}} \left({t}\right){dt}+\mathrm{2}\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{6}}} {cos}^{{n}+\mathrm{1}} \left({t}\right){dt}−\mathrm{2}\int_{\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{6}}} {cos}^{{n}} \left({t}\right){dt}\:\: \\ $$$${expresse}\:{withe}..{I} \\ $$$$\mid{An}\mid\leqslant\int\mid{x}\mid^{{n}} \sqrt{\mathrm{3}}=\sqrt{\mathrm{3}}\frac{\mathrm{2}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}} \\ $$$$\Rightarrow\Sigma{A}_{{n}} \:\:{Cv}\:{absilutly}\:\Rightarrow\Sigma{A}_{{n}} \:\:{Cv} \\ $$$$ \\ $$
Commented by abdomathmax last updated on 15/Jun/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by maths mind last updated on 15/Jun/20

$${withe}\:{pleasur} \\ $$
