Menu Close

calculste-n-0-n-2n-1-2-n-3-

Tinku Tara 0 Comments
Pin




Question Number 95216 by mathmax by abdo last updated on 24/May/20
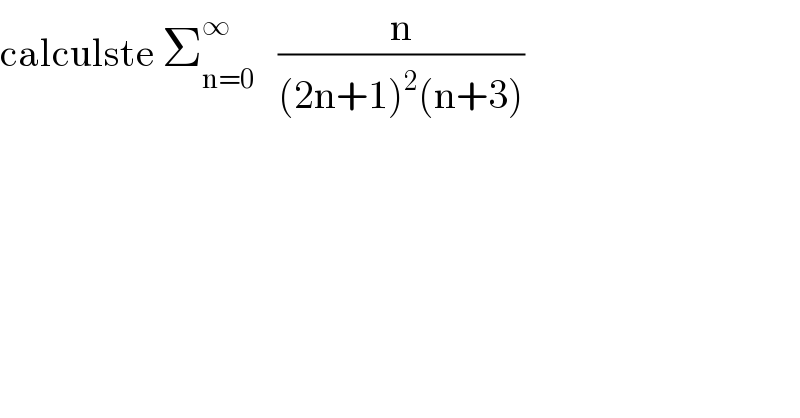
calculste Σ_(n=0) ^∞ (n/((2n+1)^2 (n+3)))
$$\mathrm{calculste}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{n}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{n}+\mathrm{3}\right)} \\ $$
Answered by abdomathmax last updated on 25/May/20
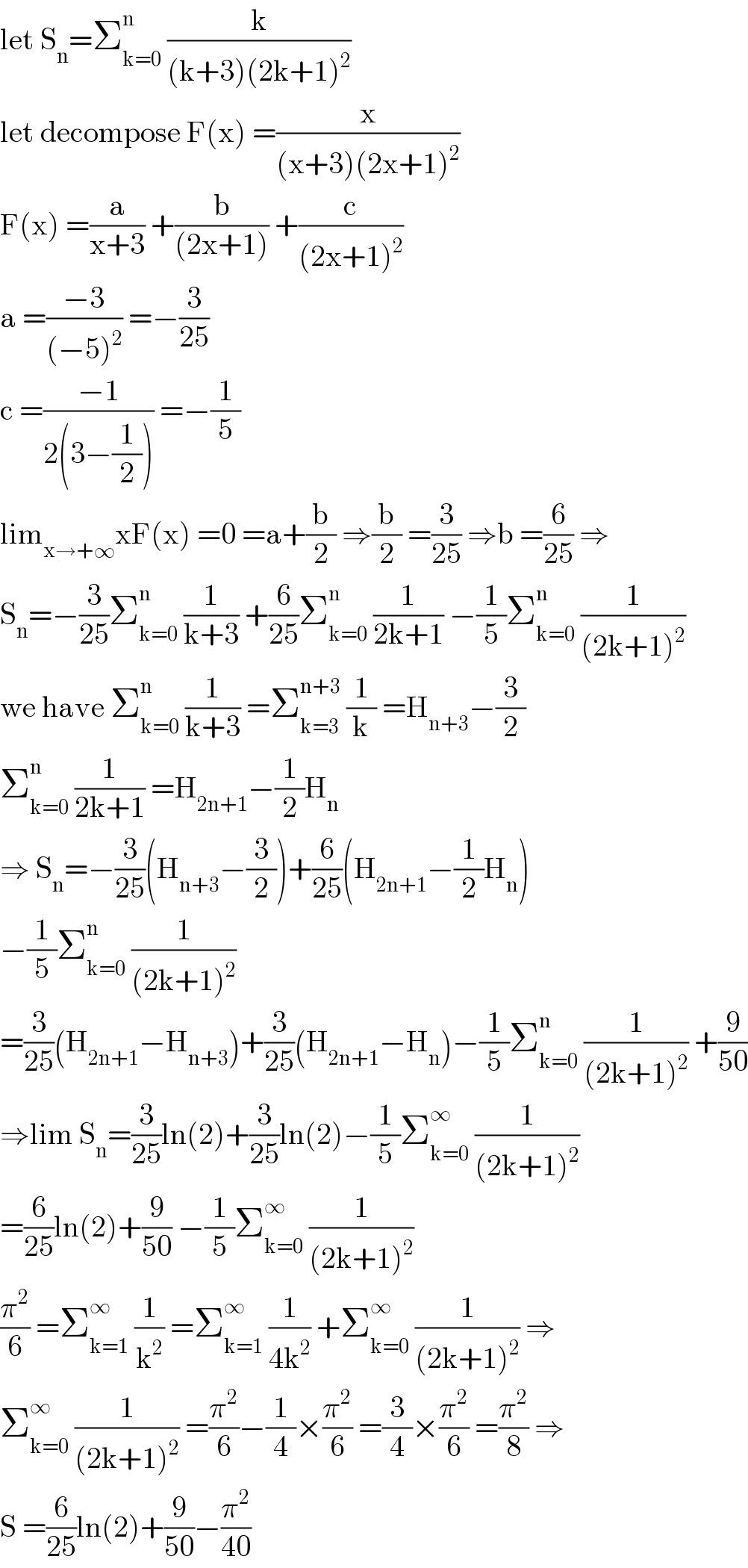
let S_n =Σ_(k=0) ^n (k/((k+3)(2k+1)^2 )) let decompose F(x) =(x/((x+3)(2x+1)^2 )) F(x) =(a/(x+3)) +(b/((2x+1))) +(c/((2x+1)^2 )) a =((−3)/((−5)^2 )) =−(3/(25)) c =((−1)/(2(3−(1/2)))) =−(1/5) lim_(x→+∞) xF(x) =0 =a+(b/2) ⇒(b/2) =(3/(25)) ⇒b =(6/(25)) ⇒ S_n =−(3/(25))Σ_(k=0) ^n (1/(k+3)) +(6/(25))Σ_(k=0) ^n (1/(2k+1)) −(1/5)Σ_(k=0) ^n (1/((2k+1)^2 )) we have Σ_(k=0) ^n (1/(k+3)) =Σ_(k=3) ^(n+3) (1/k) =H_(n+3) −(3/2) Σ_(k=0) ^n (1/(2k+1)) =H_(2n+1) −(1/2)H_n ⇒ S_n =−(3/(25))(H_(n+3) −(3/2))+(6/(25))(H_(2n+1) −(1/2)H_n ) −(1/5)Σ_(k=0) ^n (1/((2k+1)^2 )) =(3/(25))(H_(2n+1) −H_(n+3) )+(3/(25))(H_(2n+1) −H_n )−(1/5)Σ_(k=0) ^n (1/((2k+1)^2 )) +(9/(50)) ⇒lim S_n =(3/(25))ln(2)+(3/(25))ln(2)−(1/5)Σ_(k=0) ^∞ (1/((2k+1)^2 )) =(6/(25))ln(2)+(9/(50)) −(1/5)Σ_(k=0) ^∞ (1/((2k+1)^2 )) (π^2 /6) =Σ_(k=1) ^∞ (1/k^2 ) =Σ_(k=1) ^∞ (1/(4k^2 )) +Σ_(k=0) ^∞ (1/((2k+1)^2 )) ⇒ Σ_(k=0) ^∞ (1/((2k+1)^2 )) =(π^2 /6)−(1/4)×(π^2 /6) =(3/4)×(π^2 /6) =(π^2 /8) ⇒ S =(6/(25))ln(2)+(9/(50))−(π^2 /(40))
$$\mathrm{let}\:\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{k}}{\left(\mathrm{k}+\mathrm{3}\right)\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{x}}{\left(\mathrm{x}+\mathrm{3}\right)\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{3}}\:+\frac{\mathrm{b}}{\left(\mathrm{2x}+\mathrm{1}\right)}\:+\frac{\mathrm{c}}{\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{a}\:=\frac{−\mathrm{3}}{\left(−\mathrm{5}\right)^{\mathrm{2}} }\:=−\frac{\mathrm{3}}{\mathrm{25}} \\ $$$$\mathrm{c}\:=\frac{−\mathrm{1}}{\mathrm{2}\left(\mathrm{3}−\frac{\mathrm{1}}{\mathrm{2}}\right)}\:=−\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xF}\left(\mathrm{x}\right)\:=\mathrm{0}\:=\mathrm{a}+\frac{\mathrm{b}}{\mathrm{2}}\:\Rightarrow\frac{\mathrm{b}}{\mathrm{2}}\:=\frac{\mathrm{3}}{\mathrm{25}}\:\Rightarrow\mathrm{b}\:=\frac{\mathrm{6}}{\mathrm{25}}\:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} =−\frac{\mathrm{3}}{\mathrm{25}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{3}}\:+\frac{\mathrm{6}}{\mathrm{25}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{2k}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{5}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{3}}\:=\sum_{\mathrm{k}=\mathrm{3}} ^{\mathrm{n}+\mathrm{3}} \:\frac{\mathrm{1}}{\mathrm{k}}\:=\mathrm{H}_{\mathrm{n}+\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{2k}+\mathrm{1}}\:=\mathrm{H}_{\mathrm{2n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}} \\ $$$$\Rightarrow\:\mathrm{S}_{\mathrm{n}} =−\frac{\mathrm{3}}{\mathrm{25}}\left(\mathrm{H}_{\mathrm{n}+\mathrm{3}} −\frac{\mathrm{3}}{\mathrm{2}}\right)+\frac{\mathrm{6}}{\mathrm{25}}\left(\mathrm{H}_{\mathrm{2n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{H}_{\mathrm{n}} \right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{5}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{3}}{\mathrm{25}}\left(\mathrm{H}_{\mathrm{2n}+\mathrm{1}} −\mathrm{H}_{\mathrm{n}+\mathrm{3}} \right)+\frac{\mathrm{3}}{\mathrm{25}}\left(\mathrm{H}_{\mathrm{2n}+\mathrm{1}} −\mathrm{H}_{\mathrm{n}} \right)−\frac{\mathrm{1}}{\mathrm{5}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{9}}{\mathrm{50}} \\ $$$$\Rightarrow\mathrm{lim}\:\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{3}}{\mathrm{25}}\mathrm{ln}\left(\mathrm{2}\right)+\frac{\mathrm{3}}{\mathrm{25}}\mathrm{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{5}}\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{6}}{\mathrm{25}}\mathrm{ln}\left(\mathrm{2}\right)+\frac{\mathrm{9}}{\mathrm{50}}\:−\frac{\mathrm{1}}{\mathrm{5}}\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{2}} }\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{4k}^{\mathrm{2}} }\:+\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{4}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}\:\Rightarrow \\ $$$$\mathrm{S}\:=\frac{\mathrm{6}}{\mathrm{25}}\mathrm{ln}\left(\mathrm{2}\right)+\frac{\mathrm{9}}{\mathrm{50}}−\frac{\pi^{\mathrm{2}} }{\mathrm{40}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *