Question Number 162299 by mathmax by abdo last updated on 28/Dec/21
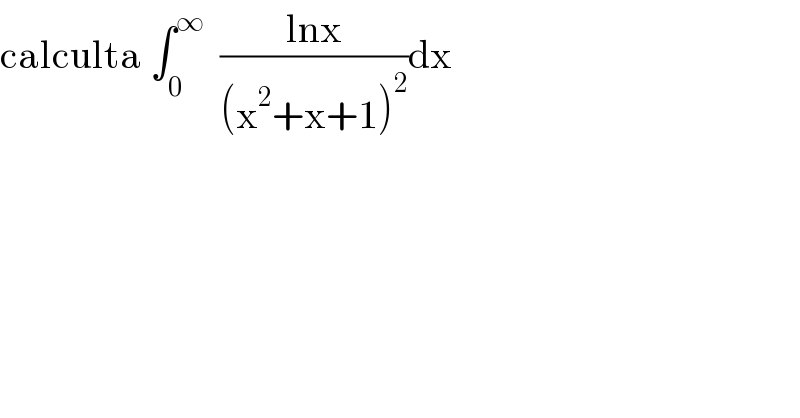
$$\mathrm{calculta}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{lnx}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Answered by Ar Brandon last updated on 24/Mar/22

$${I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}{x}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\varphi\left({z}\right)=\frac{\left(\mathrm{ln}{z}\right)^{\mathrm{2}} }{\left({z}^{\mathrm{2}} +{z}+\mathrm{1}\right)^{\mathrm{2}} }\:\:,\mathrm{Poles}:\:{z}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}={e}^{\frac{\mathrm{2}\pi}{\mathrm{3}}{i}} ,\:{z}_{\mathrm{2}} ={e}^{−\frac{\pi}{\mathrm{3}}{i}} \\ $$$$\Rightarrow\:{I}=\frac{\mathrm{1}}{\mathrm{2}}{Re}\left({Res}\left(\varphi,\:{z}_{\mathrm{1}} \right)\right) \\ $$$${Res}\:\left(\varphi,\:{z}_{\mathrm{1}} \right)=\underset{{z}\rightarrow{z}_{\mathrm{1}} } {\mathrm{lim}}\frac{{d}}{{dz}}\left\{\frac{\left(\mathrm{ln}{z}\right)^{\mathrm{2}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} }\right\} \\ $$$$=\underset{{z}\rightarrow{z}_{\mathrm{1}} } {\mathrm{lim}}\left\{\frac{\mathrm{2}{z}^{−\mathrm{1}} \left(\mathrm{ln}{z}\right)\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}\left({z}−{z}_{\mathrm{2}} \right)\left(\mathrm{ln}{z}\right)^{\mathrm{2}} }{\left({z}−{z}_{\mathrm{2}} \right)^{\mathrm{4}} }\right\} \\ $$$$=\frac{\mathrm{2}{e}^{−\frac{\mathrm{2}\pi}{\mathrm{3}}{i}} \left(\frac{\mathrm{2}\pi}{\mathrm{3}}{i}\right)\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{2}\left({i}\sqrt{\mathrm{3}}\right)\left(\frac{\mathrm{2}\pi}{\mathrm{3}}{i}\right)^{\mathrm{2}} }{\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{4}} }=\frac{{i}}{\mathrm{9}}\left(\frac{\mathrm{8}\pi^{\mathrm{2}} }{\:\mathrm{3}\sqrt{\mathrm{3}}}−\mathrm{4}\pi{e}^{−\frac{\mathrm{2}\pi}{\mathrm{3}}{i}} \right) \\ $$$$=−\frac{\mathrm{2}\sqrt{\mathrm{3}}\pi}{\mathrm{9}}+{i}\left(\frac{\mathrm{8}\pi^{\mathrm{2}} }{\mathrm{27}\sqrt{\mathrm{3}}}−\frac{\mathrm{2}\pi}{\mathrm{9}}\right) \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{Re}\left\{−\frac{\mathrm{2}\sqrt{\mathrm{3}}\pi}{\mathrm{9}}+{i}\left(\frac{\mathrm{8}\pi^{\mathrm{2}} }{\mathrm{27}\sqrt{\mathrm{3}}}−\frac{\mathrm{2}\pi}{\mathrm{9}}\right)\right\}=−\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
