Question Number 128471 by mnjuly1970 last updated on 07/Jan/21
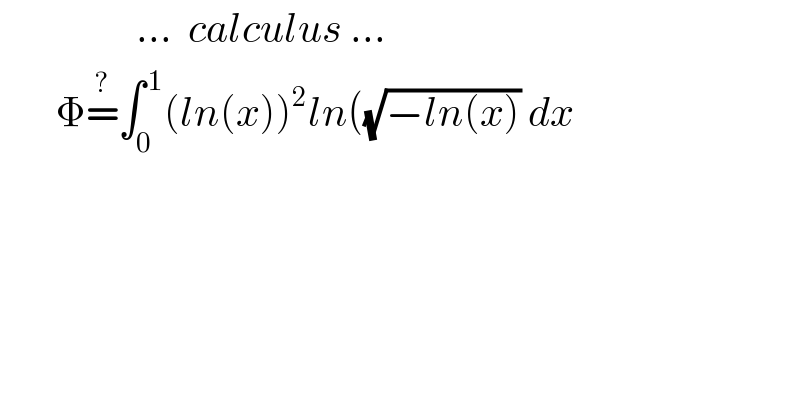
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:\:{calculus}\:… \\ $$$$\:\:\:\:\:\:\:\Phi\overset{?} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left({ln}\left({x}\right)\right)^{\mathrm{2}} {ln}\left(\sqrt{−{ln}\left({x}\right)}\:{dx}\right. \\ $$
Answered by Dwaipayan Shikari last updated on 07/Jan/21
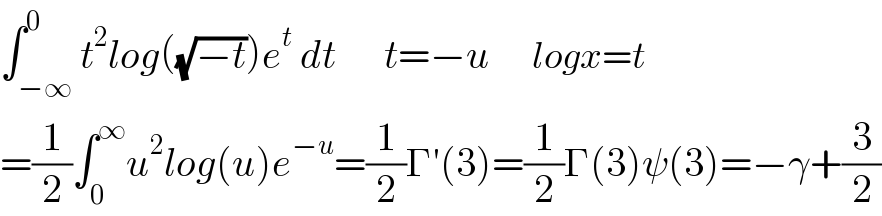
$$\int_{−\infty} ^{\mathrm{0}} {t}^{\mathrm{2}} {log}\left(\sqrt{−{t}}\right){e}^{{t}} \:{dt}\:\:\:\:\:\:{t}=−{u}\:\:\:\:\:\:\:{logx}={t} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {u}^{\mathrm{2}} {log}\left({u}\right){e}^{−{u}} =\frac{\mathrm{1}}{\mathrm{2}}\Gamma'\left(\mathrm{3}\right)=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\mathrm{3}\right)\psi\left(\mathrm{3}\right)=−\gamma+\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 07/Jan/21
$$\:\:{thank}\:{you}\:{so}\:{much}… \\ $$
Answered by mnjuly1970 last updated on 07/Jan/21
![:: −ln(x)=t Φ=(1/2)∫_0 ^( ∞) t^2 ln(t)e^(−t) dt =(1/2)[L (t^2 ln(t))]_(s=1) =(1/2) ∗((d^2 (((−γ−ln(s))/s)))/ds^2 ) =(1/2) ∗(d/ds)(((−1+γ+ln(s))/s^2 )) =(1/2)∗(((s−2s(−1+γ+ln(s)))/s^4 ))∣_(s=1) =(1/2)(3−2γ)=(3/2)−γ ....](https://www.tinkutara.com/question/Q128484.png)
$$\:\:::\:\:−{ln}\left({x}\right)={t} \\ $$$$\:\:\:\:\Phi=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} {t}^{\mathrm{2}} {ln}\left({t}\right){e}^{−{t}} {dt} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathscr{L}\:\left({t}^{\mathrm{2}} {ln}\left({t}\right)\right)\right]_{{s}=\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\:\ast\frac{{d}^{\mathrm{2}} \left(\frac{−\gamma−{ln}\left({s}\right)}{{s}}\right)}{{ds}^{\mathrm{2}} } \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\:\ast\frac{{d}}{{ds}}\left(\frac{−\mathrm{1}+\gamma+{ln}\left({s}\right)}{{s}^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\ast\left(\frac{{s}−\mathrm{2}{s}\left(−\mathrm{1}+\gamma+{ln}\left({s}\right)\right)}{{s}^{\mathrm{4}} }\right)\mid_{{s}=\mathrm{1}} \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}−\mathrm{2}\gamma\right)=\frac{\mathrm{3}}{\mathrm{2}}−\gamma\:\:\:\:…. \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\: \\ $$
