Question Number 127432 by mnjuly1970 last updated on 29/Dec/20
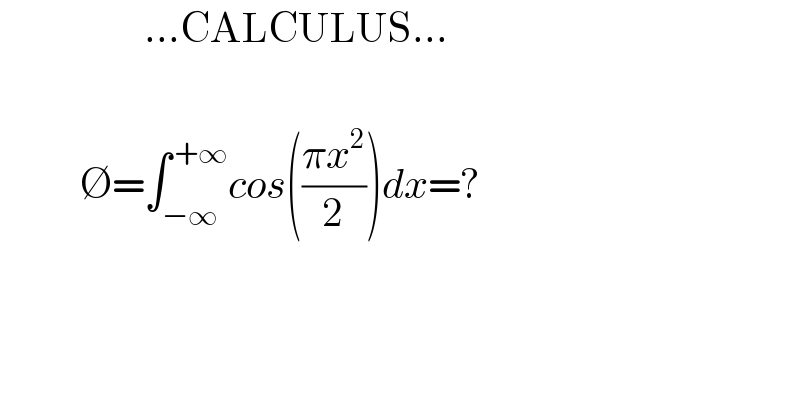
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\mathrm{CALCULUS}… \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\varnothing=\int_{−\infty} ^{\:+\infty} {cos}\left(\frac{\pi{x}^{\mathrm{2}} }{\mathrm{2}}\right){dx}=? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 29/Dec/20
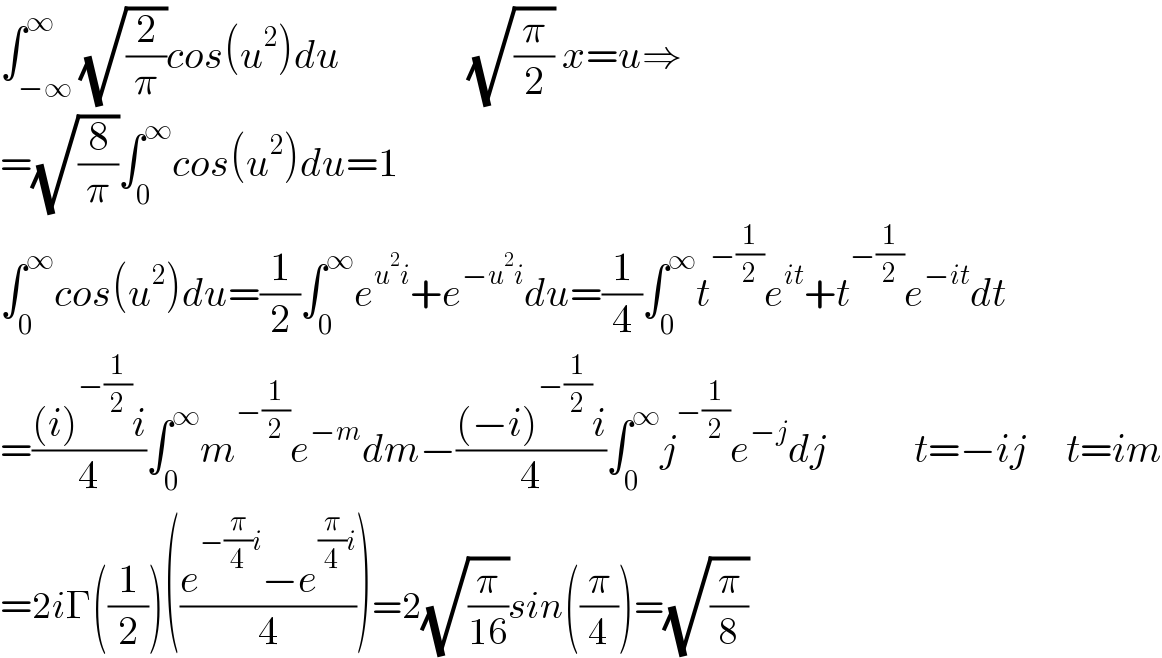
$$\int_{−\infty} ^{\infty} \sqrt{\frac{\mathrm{2}}{\pi}}{cos}\left({u}^{\mathrm{2}} \right){du}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\frac{\pi}{\mathrm{2}}}\:{x}={u}\Rightarrow \\ $$$$=\sqrt{\frac{\mathrm{8}}{\pi}}\int_{\mathrm{0}} ^{\infty} {cos}\left({u}^{\mathrm{2}} \right){du}=\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\infty} {cos}\left({u}^{\mathrm{2}} \right){du}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {e}^{{u}^{\mathrm{2}} {i}} +{e}^{−{u}^{\mathrm{2}} {i}} {du}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} {t}^{−\frac{\mathrm{1}}{\mathrm{2}}} {e}^{{it}} +{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{it}} {dt} \\ $$$$=\frac{\left({i}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {i}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} {m}^{−\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{m}} {dm}−\frac{\left(−{i}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {i}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} {j}^{−\frac{\mathrm{1}}{\mathrm{2}}} {e}^{−{j}} {dj}\:\:\:\:\:\:\:\:\:\:\:{t}=−{ij}\:\:\:\:\:{t}={im} \\ $$$$=\mathrm{2}{i}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\frac{{e}^{−\frac{\pi}{\mathrm{4}}{i}} −{e}^{\frac{\pi}{\mathrm{4}}{i}} }{\mathrm{4}}\right)=\mathrm{2}\sqrt{\frac{\pi}{\mathrm{16}}}{sin}\left(\frac{\pi}{\mathrm{4}}\right)=\sqrt{\frac{\pi}{\mathrm{8}}} \\ $$
Commented by mnjuly1970 last updated on 29/Dec/20
$${thank}\:{you}\:{master}… \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 31/Dec/20
$${Have}\:{a}\:{great}\:{year}\:{sir}! \\ $$
