Menu Close

calculus-elementary-algebra-please-solve-6x-9-1-3-7-7x-1-3-x-8-1-3-2-m-n-july-1970-

Tinku Tara 0 Comments
Pin




Question Number 116854 by mnjuly1970 last updated on 07/Oct/20
... calculus elementary algebra ... please solve :: ((6x+9))^(1/3) +((7−7x))^(1/3) +((x−8))^(1/3) =2 ...m.n.july.1970...
$$\:\:\:…\:\:\:{calculus}\:\:\:{elementary}\:\:{algebra}\:…\:\: \\ $$$$ \\ $$$$ \\ $$$$\:{please}\:{solve}\::: \\ $$$$ \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{6}{x}+\mathrm{9}}\:+\sqrt[{\mathrm{3}}]{\mathrm{7}−\mathrm{7}{x}}\:+\sqrt[{\mathrm{3}}]{{x}−\mathrm{8}}\:=\mathrm{2} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:…{m}.{n}.{july}.\mathrm{1970}… \\ $$$$\: \\ $$
Answered by MJS_new last updated on 07/Oct/20
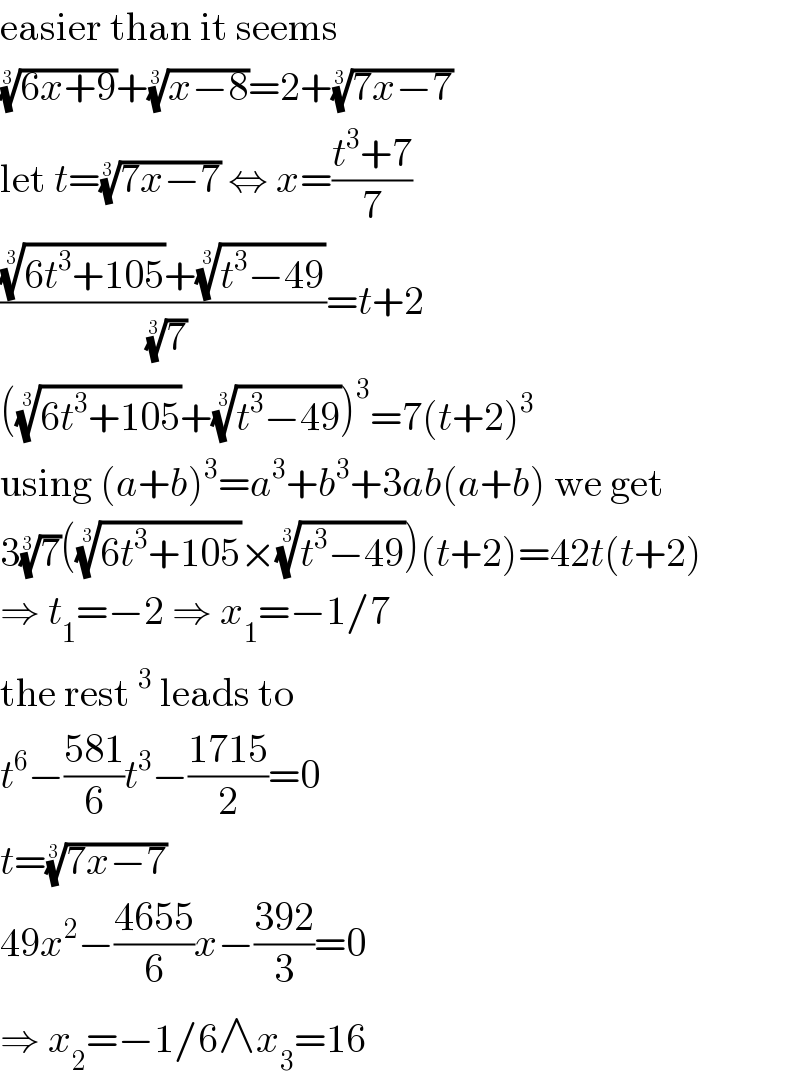
easier than it seems ((6x+9))^(1/3) +((x−8))^(1/3) =2+((7x−7))^(1/3) let t=((7x−7))^(1/3) ⇔ x=((t^3 +7)/7) ((((6t^3 +105))^(1/3) +((t^3 −49))^(1/3) )/( (7)^(1/3) ))=t+2 (((6t^3 +105))^(1/3) +((t^3 −49))^(1/3) )^3 =7(t+2)^3 using (a+b)^3 =a^3 +b^3 +3ab(a+b) we get 3(7)^(1/3) (((6t^3 +105))^(1/3) ×((t^3 −49))^(1/3) )(t+2)=42t(t+2) ⇒ t_1 =−2 ⇒ x_1 =−1/7 the rest^3 leads to t^6 −((581)/6)t^3 −((1715)/2)=0 t=((7x−7))^(1/3) 49x^2 −((4655)/6)x−((392)/3)=0 ⇒ x_2 =−1/6∧x_3 =16
$$\mathrm{easier}\:\mathrm{than}\:\mathrm{it}\:\mathrm{seems} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{6}{x}+\mathrm{9}}+\sqrt[{\mathrm{3}}]{{x}−\mathrm{8}}=\mathrm{2}+\sqrt[{\mathrm{3}}]{\mathrm{7}{x}−\mathrm{7}} \\ $$$$\mathrm{let}\:{t}=\sqrt[{\mathrm{3}}]{\mathrm{7}{x}−\mathrm{7}}\:\Leftrightarrow\:{x}=\frac{{t}^{\mathrm{3}} +\mathrm{7}}{\mathrm{7}} \\ $$$$\frac{\sqrt[{\mathrm{3}}]{\mathrm{6}{t}^{\mathrm{3}} +\mathrm{105}}+\sqrt[{\mathrm{3}}]{{t}^{\mathrm{3}} −\mathrm{49}}}{\:\sqrt[{\mathrm{3}}]{\mathrm{7}}}={t}+\mathrm{2} \\ $$$$\left(\sqrt[{\mathrm{3}}]{\mathrm{6}{t}^{\mathrm{3}} +\mathrm{105}}+\sqrt[{\mathrm{3}}]{{t}^{\mathrm{3}} −\mathrm{49}}\right)^{\mathrm{3}} =\mathrm{7}\left({t}+\mathrm{2}\right)^{\mathrm{3}} \\ $$$$\mathrm{using}\:\left({a}+{b}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\mathrm{3}{ab}\left({a}+{b}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{7}}\left(\sqrt[{\mathrm{3}}]{\mathrm{6}{t}^{\mathrm{3}} +\mathrm{105}}×\sqrt[{\mathrm{3}}]{{t}^{\mathrm{3}} −\mathrm{49}}\right)\left({t}+\mathrm{2}\right)=\mathrm{42}{t}\left({t}+\mathrm{2}\right) \\ $$$$\Rightarrow\:{t}_{\mathrm{1}} =−\mathrm{2}\:\Rightarrow\:{x}_{\mathrm{1}} =−\mathrm{1}/\mathrm{7} \\ $$$$\mathrm{the}\:\mathrm{rest}\:^{\mathrm{3}} \:\mathrm{leads}\:\mathrm{to} \\ $$$${t}^{\mathrm{6}} −\frac{\mathrm{581}}{\mathrm{6}}{t}^{\mathrm{3}} −\frac{\mathrm{1715}}{\mathrm{2}}=\mathrm{0} \\ $$$${t}=\sqrt[{\mathrm{3}}]{\mathrm{7}{x}−\mathrm{7}} \\ $$$$\mathrm{49}{x}^{\mathrm{2}} −\frac{\mathrm{4655}}{\mathrm{6}}{x}−\frac{\mathrm{392}}{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\:{x}_{\mathrm{2}} =−\mathrm{1}/\mathrm{6}\wedge{x}_{\mathrm{3}} =\mathrm{16} \\ $$
Commented by bemath last updated on 07/Oct/20
greatt
$$\mathrm{greatt} \\ $$
Commented by mnjuly1970 last updated on 07/Oct/20
thank you mr m.j.s...
$${thank}\:{you}\:\:{mr}\:{m}.{j}.{s}… \\ $$
Answered by TANMAY PANACEA last updated on 07/Oct/20
a^3 =6x+9 b^3 =7−7x c^3 =x−8 a^3 +b^3 +c^3 =8=2^3 a+b+c=(a^3 +b^3 +c^3 )^(1/3) (a+b)^3 +3(a+b)^2 c+3(a+b)c^2 +c^3 =a^3 +b^3 +c^3 3ab(a+b)+3(a+b)c(a+b+c)=0 3(a+b)(ab+ac+bc+c^2 )=0 3(a+b){a(b+c)+c(b+c)}=0 (a+b)(b+c)(a+c)=0 when a+b=0 a^3 =−b^3 6x+9=−(7−7x) 6x−7x=−16 x=16 when b+c=0 b^3 =−c^3 7−7x=−x+8 −6x=1 x=((−1)/6) when a+c=0 a^3 =−c^3 6x+9=−x+8 7x=−1 x=((−1)/7) x=16,((−1)/6) and ((−1)/7)
$${a}^{\mathrm{3}} =\mathrm{6}{x}+\mathrm{9}\:\:\:{b}^{\mathrm{3}} =\mathrm{7}−\mathrm{7}{x}\:\:\:{c}^{\mathrm{3}} ={x}−\mathrm{8} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{8}=\mathrm{2}^{\mathrm{3}} \\ $$$${a}+{b}+{c}=\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\left({a}+{b}\right)^{\mathrm{3}} +\mathrm{3}\left({a}+{b}\right)^{\mathrm{2}} {c}+\mathrm{3}\left({a}+{b}\right){c}^{\mathrm{2}} +{c}^{\mathrm{3}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \\ $$$$\mathrm{3}{ab}\left({a}+{b}\right)+\mathrm{3}\left({a}+{b}\right){c}\left({a}+{b}+{c}\right)=\mathrm{0} \\ $$$$\mathrm{3}\left({a}+{b}\right)\left({ab}+{ac}+{bc}+{c}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{3}\left({a}+{b}\right)\left\{{a}\left({b}+{c}\right)+{c}\left({b}+{c}\right)\right\}=\mathrm{0} \\ $$$$\left({a}+{b}\right)\left({b}+{c}\right)\left({a}+{c}\right)=\mathrm{0} \\ $$$${when}\:{a}+{b}=\mathrm{0} \\ $$$${a}^{\mathrm{3}} =−{b}^{\mathrm{3}} \\ $$$$\mathrm{6}{x}+\mathrm{9}=−\left(\mathrm{7}−\mathrm{7}{x}\right) \\ $$$$\mathrm{6}{x}−\mathrm{7}{x}=−\mathrm{16}\:\:\:\boldsymbol{{x}}=\mathrm{16} \\ $$$$\boldsymbol{{when}}\:\boldsymbol{{b}}+\boldsymbol{{c}}=\mathrm{0} \\ $$$$\boldsymbol{{b}}^{\mathrm{3}} =−\boldsymbol{{c}}^{\mathrm{3}} \\ $$$$\mathrm{7}−\mathrm{7}\boldsymbol{{x}}=−\boldsymbol{{x}}+\mathrm{8} \\ $$$$−\mathrm{6}{x}=\mathrm{1}\:\:\:\boldsymbol{{x}}=\frac{−\mathrm{1}}{\mathrm{6}} \\ $$$$\boldsymbol{{when}}\:\boldsymbol{{a}}+\boldsymbol{{c}}=\mathrm{0} \\ $$$$\boldsymbol{{a}}^{\mathrm{3}} =−\boldsymbol{{c}}^{\mathrm{3}} \\ $$$$\mathrm{6}\boldsymbol{{x}}+\mathrm{9}=−\boldsymbol{{x}}+\mathrm{8} \\ $$$$\mathrm{7}\boldsymbol{{x}}=−\mathrm{1}\:\:\boldsymbol{{x}}=\frac{−\mathrm{1}}{\mathrm{7}} \\ $$$$\boldsymbol{{x}}=\mathrm{16},\frac{−\mathrm{1}}{\mathrm{6}}\:{and}\:\frac{−\mathrm{1}}{\mathrm{7}} \\ $$
Commented by mnjuly1970 last updated on 07/Oct/20
thank you so much mr tanmay..
$${thank}\:{you}\:{so}\:{much}\:{mr} \\ $$$${tanmay}.. \\ $$
Commented by TANMAY PANACEA last updated on 07/Oct/20
most welcome sir
$${most}\:{welcome}\:{sir} \\ $$
Answered by 1549442205PVT last updated on 07/Oct/20
Put a=((6x+9))^(1/3) ,b=((7−7x))^(1/3) ,c=((x−8))^(1/3) We have a^3 +b^3 +c^3 =8,a+b+c=2 Hence,applying the identity : a^3 +b^3 +c^3 =(a+b+c)^3 −3(a+b)(b+c)(c+a) we get:8=8−3(a+b)(b+c)(c+a) ⇒(a+b)(a+c)(b+c)=0 i)a+b=0⇔^3 (√(6x+9))=−^3 (√(7−7x)) ⇔6x+9=−(7−7x)⇔x=16 ii)a+c=0⇔^3 (√(6x+9))=−^3 (√(x−8)) ⇔6x+9=−(x−8)⇔x=−1/7 iii)b+c=0⇔^3 (√(7−7x))=−^3 (√(x−8)) ⇔7−7x=−(x−8)⇔x=−1/6 Thus,the given equation has three roots: x∈{16,−1/7;−1/6}
$$\mathrm{Put}\:\mathrm{a}=\sqrt[{\mathrm{3}}]{\mathrm{6}{x}+\mathrm{9}}\:,\mathrm{b}=\sqrt[{\mathrm{3}}]{\mathrm{7}−\mathrm{7}{x}}\:,\mathrm{c}=\sqrt[{\mathrm{3}}]{{x}−\mathrm{8}} \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} =\mathrm{8},\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{2} \\ $$$$\mathrm{Hence},\mathrm{applying}\:\mathrm{the}\:\mathrm{identity}\:: \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} =\left(\mathrm{a}+\mathrm{b}+\mathrm{c}\right)^{\mathrm{3}} −\mathrm{3}\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{c}+\mathrm{a}\right) \\ $$$$\mathrm{we}\:\mathrm{get}:\mathrm{8}=\mathrm{8}−\mathrm{3}\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{c}+\mathrm{a}\right) \\ $$$$\Rightarrow\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}+\mathrm{c}\right)\left(\mathrm{b}+\mathrm{c}\right)=\mathrm{0} \\ $$$$\left.\mathrm{i}\right)\mathrm{a}+\mathrm{b}=\mathrm{0}\Leftrightarrow^{\mathrm{3}} \sqrt{\mathrm{6x}+\mathrm{9}}=−\:^{\mathrm{3}} \sqrt{\mathrm{7}−\mathrm{7x}} \\ $$$$\Leftrightarrow\mathrm{6x}+\mathrm{9}=−\left(\mathrm{7}−\mathrm{7x}\right)\Leftrightarrow\mathrm{x}=\mathrm{16} \\ $$$$\left.\mathrm{ii}\right)\mathrm{a}+\mathrm{c}=\mathrm{0}\Leftrightarrow^{\mathrm{3}} \sqrt{\mathrm{6x}+\mathrm{9}}=−\:^{\mathrm{3}} \sqrt{\mathrm{x}−\mathrm{8}} \\ $$$$\Leftrightarrow\mathrm{6x}+\mathrm{9}=−\left(\mathrm{x}−\mathrm{8}\right)\Leftrightarrow\mathrm{x}=−\mathrm{1}/\mathrm{7} \\ $$$$\left.\mathrm{iii}\right)\mathrm{b}+\mathrm{c}=\mathrm{0}\Leftrightarrow^{\mathrm{3}} \sqrt{\mathrm{7}−\mathrm{7x}}=−^{\mathrm{3}} \sqrt{\mathrm{x}−\mathrm{8}} \\ $$$$\Leftrightarrow\mathrm{7}−\mathrm{7x}=−\left(\mathrm{x}−\mathrm{8}\right)\Leftrightarrow\mathrm{x}=−\mathrm{1}/\mathrm{6} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{given}}\:\boldsymbol{\mathrm{equation}}\:\boldsymbol{\mathrm{ha}}\mathrm{s}\:\boldsymbol{\mathrm{three}} \\ $$$$\boldsymbol{\mathrm{roots}}:\:\:\:\:\:\:\:\mathrm{x}\in\left\{\mathrm{16},−\mathrm{1}/\mathrm{7};−\mathrm{1}/\mathrm{6}\right\} \\ $$
Commented by mnjuly1970 last updated on 07/Oct/20
very nice ...
$${very}\:{nice}\:… \\ $$
Commented by 1549442205PVT last updated on 31/Oct/20
You are welcome
$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by mnjuly1970 last updated on 08/Oct/20
we know that : a+b+c=0 ⇒a^3 +b^3 +c^3 =3abc a=((6x+9))^(1/3) , b=((7−7x))^(1/3) ,c=((x−8))^(1/3) −2 6x+9+7−7x+x−8−8−6(((x−8)^2 ))^(1/3) +12((x−8))^(1/3) =3(((6x+9))^(1/3) )(((7−7x))^(1/3) )(((x−8))^(1/3) −2) −6((x−8))^(1/3) (((x−8))^(1/3) −2)=3(((6x+9) ))^(1/3) .(((7−7x)))^(1/3) .(((x−8))^(1/3) −2) x=16 −8(x−8)=(6x+9)(7−7x) −8x+64=42x−42x^2 −63x+63 42x^2 +13x+1=0 Δ=169−168=1 x=((−13+_− 1)/(84))=((−14)/(84))=((−1)/6) , ((−1)/7) ... m.n.1970...
$${we}\:{know}\:{that}\:: \\ $$$${a}+{b}+{c}=\mathrm{0}\:\Rightarrow{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{3}{abc} \\ $$$${a}=\sqrt[{\mathrm{3}}]{\mathrm{6}{x}+\mathrm{9}}\:,\:{b}=\sqrt[{\mathrm{3}}]{\mathrm{7}−\mathrm{7}{x}}\:,{c}=\sqrt[{\mathrm{3}}]{{x}−\mathrm{8}}\:−\mathrm{2}\: \\ $$$$\mathrm{6}{x}+\mathrm{9}+\mathrm{7}−\mathrm{7}{x}+{x}−\mathrm{8}−\mathrm{8}−\mathrm{6}\sqrt[{\mathrm{3}}]{\left({x}−\mathrm{8}\right)^{\mathrm{2}} }\:+\mathrm{12}\sqrt[{\mathrm{3}}]{{x}−\mathrm{8}} \\ $$$$=\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\mathrm{6}{x}+\mathrm{9}}\:\right)\left(\sqrt[{\mathrm{3}}]{\mathrm{7}−\mathrm{7}{x}}\:\right)\left(\sqrt[{\mathrm{3}}]{{x}−\mathrm{8}}\:−\mathrm{2}\right) \\ $$$$−\mathrm{6}\sqrt[{\mathrm{3}}]{{x}−\mathrm{8}}\:\left(\sqrt[{\mathrm{3}}]{{x}−\mathrm{8}}\:−\mathrm{2}\right)=\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\left.\mathrm{6}{x}+\mathrm{9}\right)\:}\:.\left(\sqrt[{\mathrm{3}}]{\left.\mathrm{7}−\mathrm{7}{x}\right)}\:.\left(\sqrt[{\mathrm{3}}]{{x}−\mathrm{8}}\:−\mathrm{2}\right)\right.\right. \\ $$$${x}=\mathrm{16} \\ $$$$ \\ $$$$−\mathrm{8}\left({x}−\mathrm{8}\right)=\left(\mathrm{6}{x}+\mathrm{9}\right)\left(\mathrm{7}−\mathrm{7}{x}\right) \\ $$$$−\mathrm{8}{x}+\mathrm{64}=\mathrm{42}{x}−\mathrm{42}{x}^{\mathrm{2}} −\mathrm{63}{x}+\mathrm{63} \\ $$$$\mathrm{42}{x}^{\mathrm{2}} +\mathrm{13}{x}+\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\mathrm{169}−\mathrm{168}=\mathrm{1} \\ $$$${x}=\frac{−\mathrm{13}\underset{−} {+}\mathrm{1}}{\mathrm{84}}=\frac{−\mathrm{14}}{\mathrm{84}}=\frac{−\mathrm{1}}{\mathrm{6}}\:\:\:,\:\frac{−\mathrm{1}}{\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:…\:\:{m}.{n}.\mathrm{1970}… \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *