Question Number 114304 by mnjuly1970 last updated on 18/Sep/20
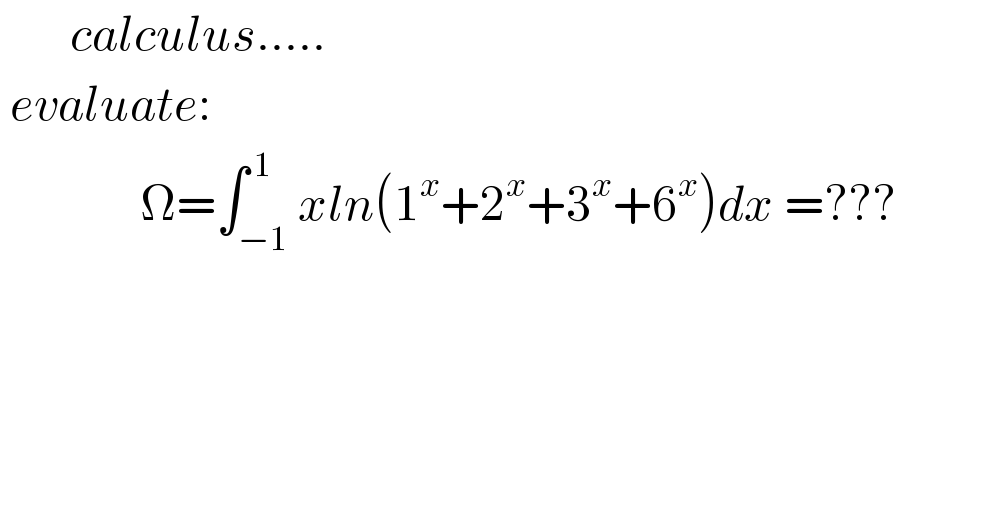
Commented by MJS_new last updated on 18/Sep/20
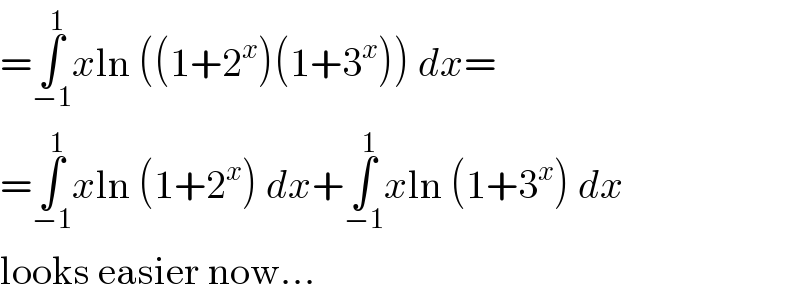
Commented by Dwaipayan Shikari last updated on 18/Sep/20

Commented by Dwaipayan Shikari last updated on 18/Sep/20
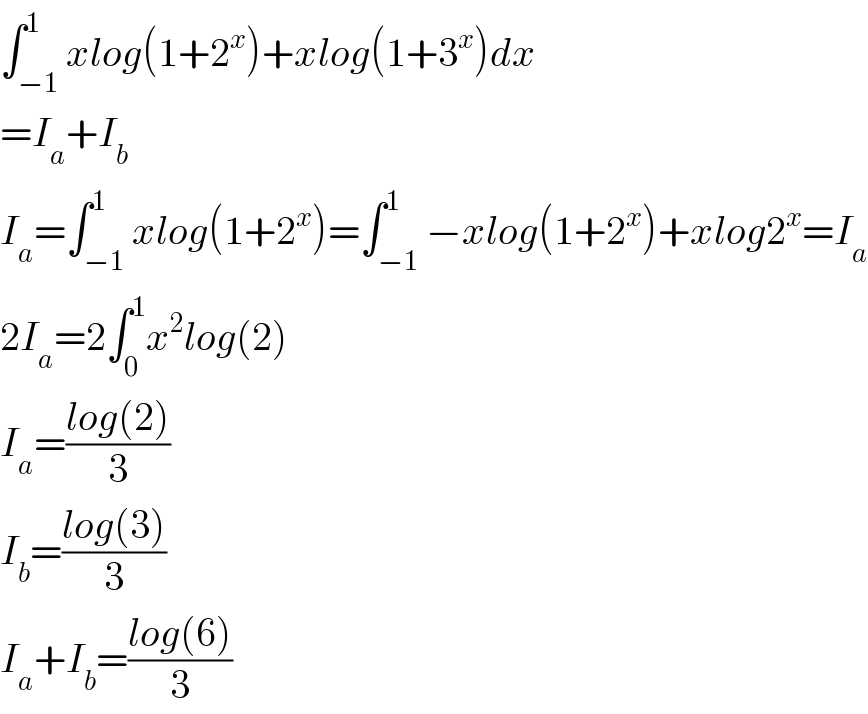
Commented by MJS_new last updated on 18/Sep/20

Commented by mnjuly1970 last updated on 18/Sep/20

Commented by mnjuly1970 last updated on 18/Sep/20

