Question Number 113198 by mnjuly1970 last updated on 11/Sep/20
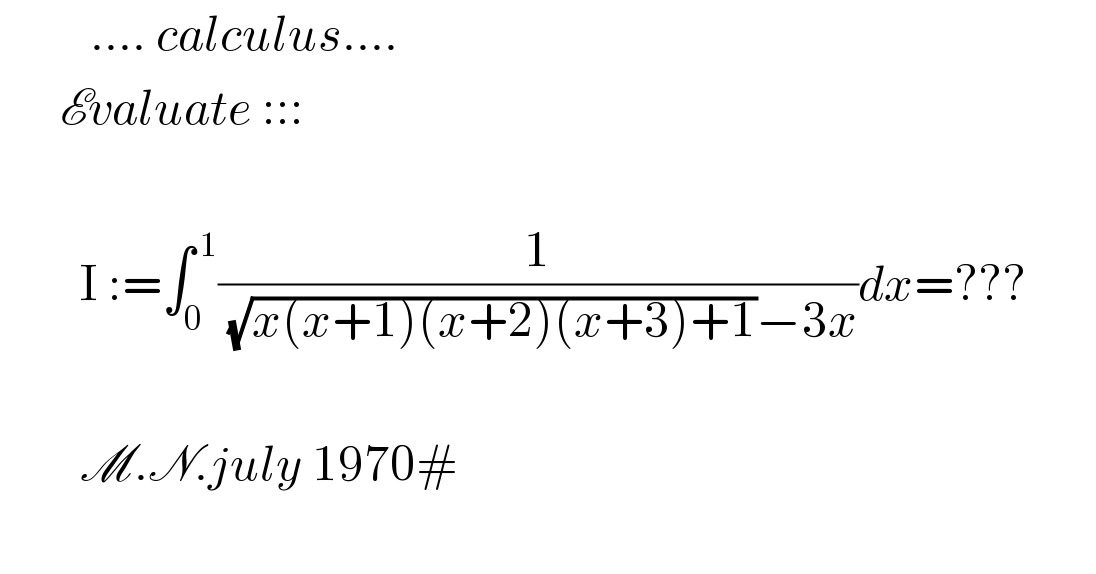
$$\:\:\:\:\:\:\:\:\:….\:{calculus}…. \\ $$$$\:\:\:\:\:\:\mathscr{E}{valuate}\:::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\mathrm{I}\::=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{{x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)+\mathrm{1}}−\mathrm{3}{x}}{dx}=??? \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\mathscr{M}.\mathscr{N}.{july}\:\mathrm{1970}# \\ $$$$\:\: \\ $$
Answered by MJS_new last updated on 11/Sep/20
![x(x+1)(x+2)(x+3)+1= =(x^2 +3x+1)^2 for 0≤x≤1: (√((x^2 +3x+1)^2 ))=x^2 +3x+1 ⇒ the integral resolves to ∫_0 ^1 (dx/(x^2 +1))=[arctan x]_0 ^1 =(π/4)](https://www.tinkutara.com/question/Q113255.png)
$${x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)+\mathrm{1}= \\ $$$$=\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{for}\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}:\:\sqrt{\left({x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} }={x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{integral}\:\mathrm{resolves}\:\mathrm{to} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}=\left[\mathrm{arctan}\:{x}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 12/Sep/20
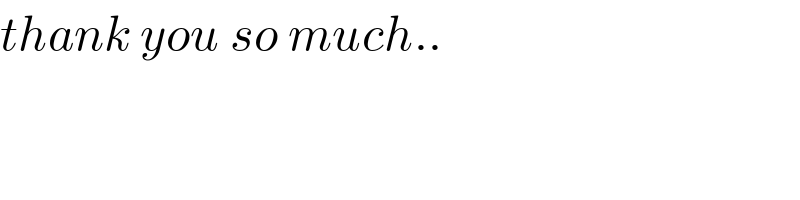
$${thank}\:{you}\:{so}\:{much}.. \\ $$
