calculus-evaluate-i-0-1-t-2-ln-t-ln-1-t-dt-ii-1-4-iii-0-pi-8-ln-tan-x-dx-

Question Number 114302 by mnjuly1970 last updated on 18/Sep/20

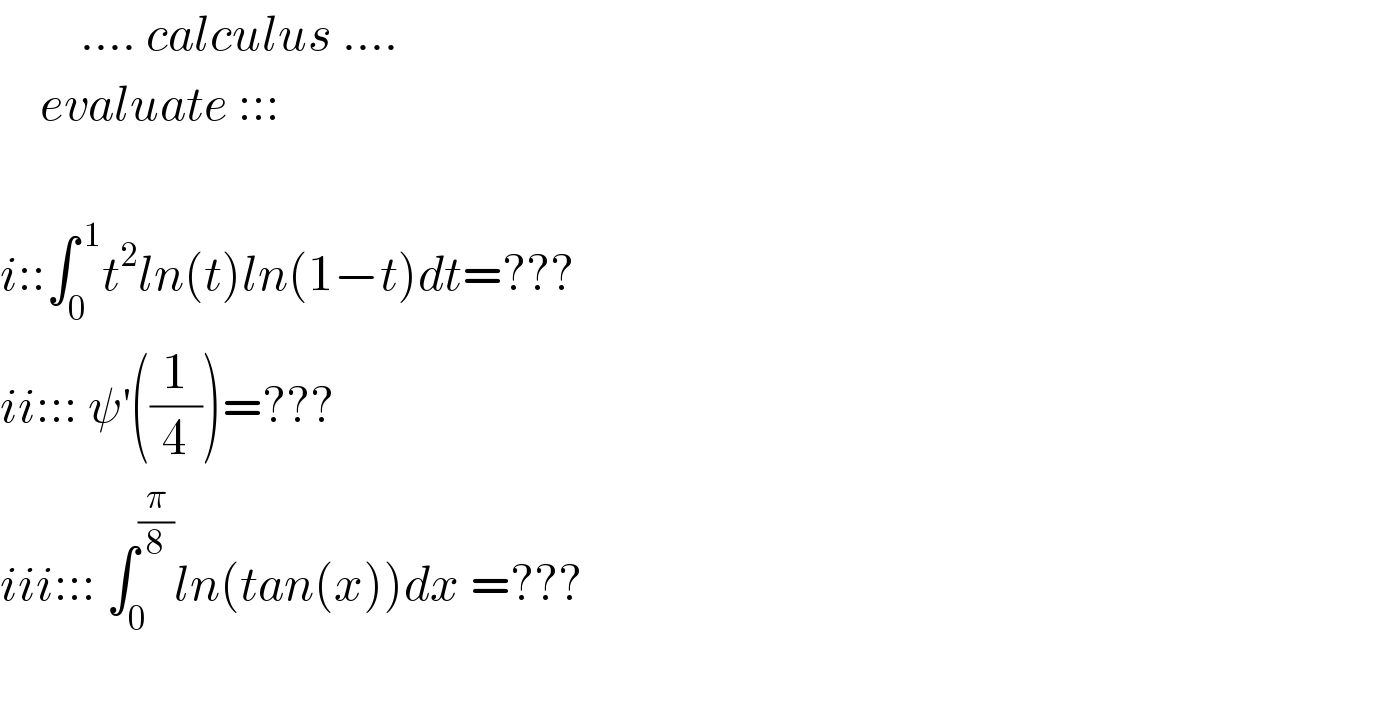
.... calculus .... evaluate ::: i::∫_0 ^( 1) t^2 ln(t)ln(1−t)dt=??? ii::: ψ^′ ((1/4))=??? iii::: ∫_0 ^(π/8) ln(tan(x))dx =???

\dots . c a l c u l u s \dots .

e v a l u a t e :::

i :: \int_{0}^{1} t^{2} l n (t) l n (1 - t) d t = ? ? ?

i i ::: ψ^{^{'}} (\frac{1}{4}) = ? ? ?

i i i ::: \int_{0}^{\frac{π}{8}} l n (t a n (x)) d x = ? ? ?

Commented by MJS_new last updated on 18/Sep/20

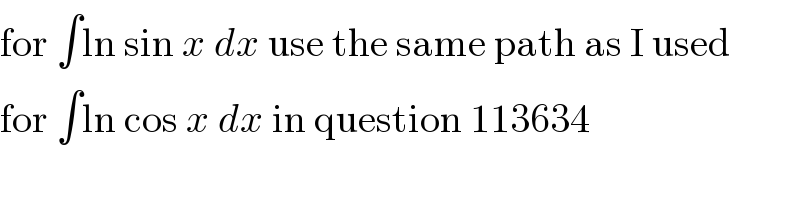
for ∫ln sin x dx use the same path as I used for ∫ln cos x dx in question 113634

for \int \ln \sin x d x use the same path as I used

for \int \ln \cos x d x in question 113634

Commented by MJS_new last updated on 18/Sep/20

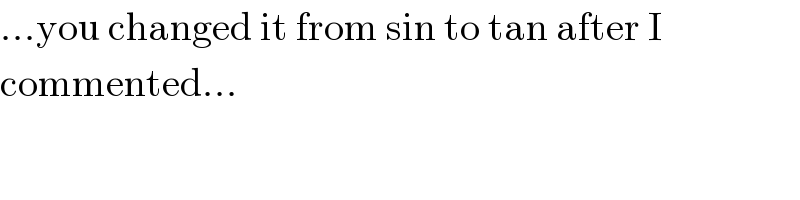
...you changed it from sin to tan after I commented...

\dots you changed it from \sin to \tan after I

commented \dots

Answered by Olaf last updated on 18/Sep/20

I_n = ∫_0 ^1 x^n lnxdx I_n = [(x^(n+1) /(n+1))lnx]_0 ^1 − ∫_0 ^1 (x^(n+1) /(n+1)).(dx/x) I_n = −[(x^(n+1) /((n+1)^2 ))]_0 ^1 = −(1/((n+1)^2 )) (1/(1−t)) = Σ_(n=0) ^∞ t^n ln∣1−t∣ = −Σ_(n=0) ^∞ (t^(n+1) /(n+1)) if ∣t∣<1 I = ∫_0 ^1 t^2 ln(t)ln(1−t)dt I = −∫_0 ^1 t^2 ln(t)Σ_(n=0) ^∞ (t^(n+1) /(n+1))dt I = −Σ_(n=0) ^∞ (1/(n+1))∫_0 ^1 t^(n+3) lntdt I = −Σ_(n=0) ^∞ (I_(n+3) /(n+1)) = Σ_(n=0) ^∞ (1/((n+1)(n+4)^2 )) I = Σ_(n=1) ^∞ (1/(n(n+3)^2 )) (1/(n(n+3)^2 )) = (1/(9n))−(1/(9(n+3)))−(1/(3(n+3)^2 )) I = (1/9)((1/1)+(1/2)+(1/3))−(1/3)Σ_(n=1() ^∞ (1/(n+3)^2 )) I = ((11)/(54))−(1/3)Σ_(n=4) ^∞ (1/n^2 ) With Σ_(n=1) ^∞ (1/n^2 ) = ξ(2) = (π^2 /6) I = ((11)/(54))−(1/3)((π^2 /6)−(1/1^2 )−(1/2^2 )−(1/3^2 )) I = ((71)/(108))−(π^2 /(18)) ≈ 0,109096051

I_{n} = \int_{0}^{1} x^{n} \ln x d x

I_{n} = {[\frac{x^{n + 1}}{n + 1} \ln x]}_{0}^{1} - \int_{0}^{1} \frac{x^{n + 1}}{n + 1} . \frac{d x}{x}

I_{n} = - {[\frac{x^{n + 1}}{{(n + 1)}^{2}}]}_{0}^{1} = - \frac{1}{{(n + 1)}^{2}}

\frac{1}{1 - t} = \underset{n = 0}{\sum^{\infty}} t^{n}

\ln ∣ 1 - t ∣ = - \underset{n = 0}{\sum^{\infty}} \frac{t^{n + 1}}{n + 1} if ∣ t ∣< 1

I = \int_{0}^{1} t^{2} \ln (t) \ln (1 - t) d t

I = - \int_{0}^{1} t^{2} \ln (t) \underset{n = 0}{\sum^{\infty}} \frac{t^{n + 1}}{n + 1} d t

I = - \underset{n = 0}{\sum^{\infty}} \frac{1}{n + 1} \int_{0}^{1} t^{n + 3} \ln t d t

I = - \underset{n = 0}{\sum^{\infty}} \frac{I_{n + 3}}{n + 1} = \underset{n = 0}{\sum^{\infty}} \frac{1}{(n + 1) {(n + 4)}^{2}}

I = \underset{n = 1}{\sum^{\infty}} \frac{1}{n {(n + 3)}^{2}}

\frac{1}{n {(n + 3)}^{2}} = \frac{1}{9 n} - \frac{1}{9 (n + 3)} - \frac{1}{3 {(n + 3)}^{2}}

I = \frac{1}{9} (\frac{1}{1} + \frac{1}{2} + \frac{1}{3}) - \frac{1}{3} \underset{n = 1 (}{\sum^{\infty}} \frac{1}{{n + 3)}^{2}}

I = \frac{11}{54} - \frac{1}{3} \underset{n = 4}{\sum^{\infty}} \frac{1}{n^{2}}

With \underset{n = 1}{\sum^{\infty}} \frac{1}{n^{2}} = ξ (2) = \frac{π^{2}}{6}

I = \frac{11}{54} - \frac{1}{3} (\frac{π^{2}}{6} - \frac{1}{1^{2}} - \frac{1}{2^{2}} - \frac{1}{3^{2}})

I = \frac{71}{108} - \frac{π^{2}}{18} \approx 0, 109096051

Commented by mnjuly1970 last updated on 19/Sep/20

very good .thank you sir your work is admirable...

v e r y g o o d . t h a n k y o u s i r

y o u r w o r k i s a d m i r a b l e \dots

Answered by mathmax by abdo last updated on 19/Sep/20

3) I =∫_0 ^(π/8) ln(tanx)dx by parts I= [xln(tanx)]_0 ^(π/8) −∫_0 ^(π/8) x×((1+tan^2 x)/(tanx))dx =(π/8)ln((√2)−1)−∫_0 ^(π/8) (x/(tanx))dx−∫_0 ^(π/8) tanx dx ∫_0 ^(π/8) tanx dx =[−ln∣cosx∣]_0 ^(π/8) =−ln(((√2)/2)) =−ln((1/( (√2)))) =((ln2)/2) A =∫_0 ^(π/8) (x/(tanx))dx ⇒ A =_(tanx=t) ∫_0 ^((√2)−1) ((arctant)/t)(dt/(1+t^2 )) =∫_0 ^((√2)−1) arctan(t){(1/t)−(t/(1+t^2 ))}dt =∫_0 ^((√2)−1) ((arctant)/t)dt −∫_0 ^((√2)−1) (t/(1+t^2 )) arctan(t)dt by parts ∫_0 ^((√2)−1) (t/(1+t^2 )) arctan(t)dt =[(1/2)ln(1+t^2 )arctant]_0 ^((√2)−1) −∫_0 ^((√2)−1) (1/2)ln(1+t^2 )×(dt/(1+t^2 )) =(1/2)ln(4−2(√2)) arctan((√2)−1) −(1/2) ∫_0 ^((√2)−1) ((ln(1+t^2 ))/(1+t^2 )) dt we considere f(a) =∫_0 ^((√2)−1) ((ln(1+at^2 ))/(1+t^2 ))dt with a>0 f^′ (a) =∫_0 ^((√2)−1) (t^2 /((1+t^2 )(1+at^2 ))) dt let decompose F(t) =(t^2 /((t^2 +1)(at^2 +1))) ⇒F(t)=((αt +β)/(t^2 +1)) +((mt+n)/(at^2 +1)) ⇒ F(−t)=F(t) ⇒((−αt +β)/(t^2 +1)) +((−mt +n)/(at^2 +1)) =F(t)⇒α=m=0 ⇒ F(t)=(β/(t^2 +1)) +(n/(at^2 +1)) we haveF(0) =0 =β+n ⇒n=−β lim_(t→+∞) t^2 F(t) =(1/a) =β +(n/a) ⇒1=aβ +n ⇒1=aβ−β =(a−1)β ⇒β =(1/(a−1)) ⇒F(t) =(1/((a−1)(t^2 +1)))−(1/((a−1)(at^2 +1))) ⇒ f^′ (a) =(1/(a−1)) ∫_0 ^((√2)−1) (dt/(t^2 +1))−(1/(a−1))∫_0 ^((√2)−1 ) (dt/(at^2 +1))(→(√a)t =u) =((arctan((√2)−1))/(a−1))−(1/(a−1)) ∫_0 ^(((√2)−1)(√a)) (du/( (√a)(u^2 +1))) =((arctan((√2)−1))/(a−1))−(1/( (√a)(a−1)))arctan(((√2)−1)(√a)) ⇒ f(a) =arctan((√2)−1)ln∣a−1∣−∫ ((arctan(((√2)−1)(√a)))/( (√a)(a−1))) da +C ....be continued...

3) I = \int_{0}^{\frac{π}{8}} \ln (tanx) dx by parts I = {[xln (tanx)]}_{0}^{\frac{π}{8}} - \int_{0}^{\frac{π}{8}} x \times \frac{1 + \tan^{2} x}{tanx} dx

= \frac{π}{8} \ln (\sqrt{2} - 1) - \int_{0}^{\frac{π}{8}} \frac{x}{tanx} dx - \int_{0}^{\frac{π}{8}} tanx dx

\int_{0}^{\frac{π}{8}} tanx dx = {[- \ln ∣ cosx ∣]}_{0}^{\frac{π}{8}} = - \ln (\frac{\sqrt{2}}{2}) = - \ln (\frac{1}{\sqrt{2}}) = \frac{\ln 2}{2}

A = \int_{0}^{\frac{π}{8}} \frac{x}{tanx} dx \Rightarrow A =_{tanx = t} \int_{0}^{\sqrt{2} - 1} \frac{arctant}{t} \frac{dt}{1 + t^{2}}

= \int_{0}^{\sqrt{2} - 1} \arctan (t) {\frac{1}{t} - \frac{t}{1 + t^{2}}} dt = \int_{0}^{\sqrt{2} - 1} \frac{arctant}{t} dt - \int_{0}^{\sqrt{2} - 1} \frac{t}{1 + t^{2}} \arctan (t) dt

by parts \int_{0}^{\sqrt{2} - 1} \frac{t}{1 + t^{2}} \arctan (t) dt = {[\frac{1}{2} \ln (1 + t^{2}) arctant]}_{0}^{\sqrt{2} - 1}

- \int_{0}^{\sqrt{2} - 1} \frac{1}{2} \ln (1 + t^{2}) \times \frac{dt}{1 + t^{2}} = \frac{1}{2} \ln (4 - 2 \sqrt{2}) \arctan (\sqrt{2} - 1)

- \frac{1}{2} \int_{0}^{\sqrt{2} - 1} \frac{\ln (1 + t^{2})}{1 + t^{2}} dt we considere f (a) = \int_{0}^{\sqrt{2} - 1} \frac{\ln (1 + {at}^{2})}{1 + t^{2}} dt

with a > 0

f^{^{'}} (a) = \int_{0}^{\sqrt{2} - 1} \frac{t^{2}}{(1 + t^{2}) (1 + {at}^{2})} dt let decompose

F (t) = \frac{t^{2}}{(t^{2} + 1) ({at}^{2} + 1)} \Rightarrow F (t) = \frac{α t + β}{t^{2} + 1} + \frac{mt + n}{{at}^{2} + 1} \Rightarrow

F (- t) = F (t) \Rightarrow \frac{- α t + β}{t^{2} + 1} + \frac{- mt + n}{{at}^{2} + 1} = F (t) \Rightarrow α = m = 0 \Rightarrow

F (t) = \frac{β}{t^{2} + 1} + \frac{n}{{at}^{2} + 1} we haveF (0) = 0 = β + n \Rightarrow n = - β

\lim_{t \to + \infty} t^{2} F (t) = \frac{1}{a} = β + \frac{n}{a} \Rightarrow 1 = a β + n \Rightarrow 1 = a β - β = (a - 1) β

\Rightarrow β = \frac{1}{a - 1} \Rightarrow F (t) = \frac{1}{(a - 1) (t^{2} + 1)} - \frac{1}{(a - 1) ({at}^{2} + 1)} \Rightarrow

f^{^{'}} (a) = \frac{1}{a - 1} \int_{0}^{\sqrt{2} - 1} \frac{dt}{t^{2} + 1} - \frac{1}{a - 1} \int_{0}^{\sqrt{2} - 1} \frac{dt}{{at}^{2} + 1} (\to \sqrt{a} t = u)

= \frac{\arctan (\sqrt{2} - 1)}{a - 1} - \frac{1}{a - 1} \int_{0}^{(\sqrt{2} - 1) \sqrt{a}} \frac{du}{\sqrt{a} (u^{2} + 1)}

= \frac{\arctan (\sqrt{2} - 1)}{a - 1} - \frac{1}{\sqrt{a} (a - 1)} \arctan ((\sqrt{2} - 1) \sqrt{a}) \Rightarrow

f (a) = \arctan (\sqrt{2} - 1) \ln ∣ a - 1 ∣ - \int \frac{\arctan ((\sqrt{2} - 1) \sqrt{a})}{\sqrt{a} (a - 1)} da + C

\dots . be continued \dots

Answered by maths mind last updated on 19/Sep/20

∫_0 ^(π/8) ln(tg(x))dx ln(tg(x))=−2Σ_(k≥0) ((cos(2(2k+1)x))/(2k+1)) =∫_0 ^(π/8) (−2Σ_(k≥0) ((cos(2(2k+1)x))/(2k+1)))dx =Σ_(k≥0) −(1/((2k+1)^2 ))sin((((2k+1)π)/4)) =−Σ_(k≥0) (1/((2k+1)^2 ))sin(((kπ)/2)+(π/4)) =−Σ_(k≥0) ((sin((π/4)))/((8k+1)^2 ))−Σ_(k≥0) ((sin((π/4)))/((8k+3)^2 ))+Σ((sin((π/4)))/((8k+5)^2 ))+Σ((sin((π/4)))/((8k+7)^2 )) =((sin((π/4)))/(64)){−Σ(1/((k+(1/8))^2 ))−Σ(1/((k+(3/8))^2 ))+Σ(1/((k+(5/8))^2 ))+Σ(1/((k+(7/8))^2 ))} Σ_(n≥0) (1/((n+a)^p ))=ζ(a,p) hurwitz zeta function =((sin((π/4)))/(64)){−ζ((1/8),2)−ζ((3/8),2)+ζ((5/8),2)+ζ((7/8),2)}

\int_{0}^{\frac{π}{8}} l n (t g (x)) d x

l n (t g (x)) = - 2 \sum_{k ⩾ 0} \frac{c o s (2 (2 k + 1) x)}{2 k + 1}

= \int_{0}^{\frac{π}{8}} (- 2 \sum_{k ⩾ 0} \frac{c o s (2 (2 k + 1) x)}{2 k + 1}) d x

= \sum_{k ⩾ 0} - \frac{1}{{(2 k + 1)}^{2}} s i n (\frac{(2 k + 1) π}{4})

= - \sum_{k ⩾ 0} \frac{1}{{(2 k + 1)}^{2}} s i n (\frac{k π}{2} + \frac{π}{4})

= - \sum_{k ⩾ 0} \frac{s i n (\frac{π}{4})}{{(8 k + 1)}^{2}} - \sum_{k ⩾ 0} \frac{s i n (\frac{π}{4})}{{(8 k + 3)}^{2}} + Σ \frac{s i n (\frac{π}{4})}{{(8 k + 5)}^{2}} + Σ \frac{s i n (\frac{π}{4})}{{(8 k + 7)}^{2}}

= \frac{s i n (\frac{π}{4})}{64} {- Σ \frac{1}{{(k + \frac{1}{8})}^{2}} - Σ \frac{1}{{(k + \frac{3}{8})}^{2}} + Σ \frac{1}{{(k + \frac{5}{8})}^{2}} + Σ \frac{1}{{(k + \frac{7}{8})}^{2}}}

\sum_{n ⩾ 0} \frac{1}{{(n + a)}^{p}} = ζ (a, p) h u r w i t z z e t a f u n c t i o n

= \frac{s i n (\frac{π}{4})}{64} {- ζ (\frac{1}{8}, 2) - ζ (\frac{3}{8}, 2) + ζ (\frac{5}{8}, 2) + ζ (\frac{7}{8}, 2)}

Commented by mnjuly1970 last updated on 19/Sep/20

v e r y n i c e s i r . t h a n k s a l o t . .

Answered by Olaf last updated on 19/Sep/20

iii... I = ∫_0 ^(π/8) ln(tanx)dx tan2θ = ((2tanθ)/(1−tan^2 θ)) with θ = (π/8), tan(π/4) = ((2tan(π/8))/(1−tan^2 (π/8))) = 1 tan^2 (π/8)+2tan(π/8)−1 = 0 ⇒ tan(π/8) = (√2)−1 Now u = tanx du = (1+tan^2 x)dx = (1+u^2 )dx I = ∫_0 ^((√2)−1) ((lnu)/(1+u^2 ))du I = ∫_0 ^((√2)−1) lnuΣ_(n=0) ^∞ (−1)^n u^(2n) du I = Σ_(n=0) ^∞ (−1)^n ∫_0 ^((√2)−1) u^(2n) lnudu I = Σ_(n=0) ^∞ (−1)^n ([(u^(2n+1) /(2n+1))lnu]_0 ^((√2)−1) −∫_0 ^((√2)−1) (u^(2n+1) /(2n+1)).(du/u)) I = Σ_(n=0) ^∞ (−1)^n (ln((√2)−1)[((((√2)−1)^(2n+1) )/(2n+1))]−[(u^(2n+1) /((2n+1)^2 ))]_0 ^((√2)−1) ) I = Σ_(n=0) ^∞ (−1)^n (ln((√2)−1)[((((√2)−1)^(2n+1) )/(2n+1))]−[((((√2)−1)^(2n+1) )/((2n+1)^2 ))]) arctanx = Σ_(n=0) ^∞ (−1)^n (x^(2n+1) /(2n+1)) I = ln((√2)−1)arctan((√2)−1)−Σ_(n=0) ^∞ (−1)^n ((((√2)−1)^(2n+1) )/((2n+1)^2 )) I = (π/8)ln((√2)−1)−Σ_(n=0) ^∞ (−1)^n ((((√2)−1)^(2n+1) )/((2n+1)^2 )) I think we cannot simplify

i i i \dots

I = \int_{0}^{\frac{π}{8}} \ln (\tan x) d x

\tan 2 θ = \frac{2 \tan θ}{1 - \tan^{2} θ}

with θ = \frac{π}{8}, \tan \frac{π}{4} = \frac{2 \tan \frac{π}{8}}{1 - \tan^{2} \frac{π}{8}} = 1

\tan^{2} \frac{π}{8} + 2 \tan \frac{π}{8} - 1 = 0

\Rightarrow \tan \frac{π}{8} = \sqrt{2} - 1

Now u = \tan x

d u = (1 + \tan^{2} x) d x = (1 + u^{2}) d x

I = \int_{0}^{\sqrt{2} - 1} \frac{\ln u}{1 + u^{2}} d u

I = \int_{0}^{\sqrt{2} - 1} \ln u \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} u^{2 n} d u

I = \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} \int_{0}^{\sqrt{2} - 1} u^{2 n} \ln u d u

I = \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} ({[\frac{u^{2 n + 1}}{2 n + 1} \ln u]}_{0}^{\sqrt{2} - 1} - \int_{0}^{\sqrt{2} - 1} \frac{u^{2 n + 1}}{2 n + 1} . \frac{d u}{u})

I = \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} (\ln (\sqrt{2} - 1) [\frac{{(\sqrt{2} - 1)}^{2 n + 1}}{2 n + 1}] - {[\frac{u^{2 n + 1}}{{(2 n + 1)}^{2}}]}_{0}^{\sqrt{2} - 1})

I = \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} (\ln (\sqrt{2} - 1) [\frac{{(\sqrt{2} - 1)}^{2 n + 1}}{2 n + 1}] - [\frac{{(\sqrt{2} - 1)}^{2 n + 1}}{{(2 n + 1)}^{2}}])

\arctan x = \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} \frac{x^{2 n + 1}}{2 n + 1}

I = \ln (\sqrt{2} - 1) \arctan (\sqrt{2} - 1) - \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} \frac{{(\sqrt{2} - 1)}^{2 n + 1}}{{(2 n + 1)}^{2}}

I = \frac{π}{8} \ln (\sqrt{2} - 1) - \underset{n = 0}{\sum^{\infty}} {(- 1)}^{n} \frac{{(\sqrt{2} - 1)}^{2 n + 1}}{{(2 n + 1)}^{2}}

I think we cannot simplify

Answered by mathmax by abdo last updated on 20/Sep/20

A =∫_0 ^1 x^2 ln(x)ln(1−x)dx we have (d/dx)ln(1−x) =((−1)/(1−x))=−Σ_(n=0) ^∞ x^n ⇒ln(1−x) =−Σ_(n=0) ^∞ (x^(n+1) /(n+1)) +c (c=0) =−Σ_(n=1) ^∞ (x^n /n) ⇒ A =−∫_0 ^1 x^2 lnx(Σ_(n=1) ^∞ (x^n /n))dx =−Σ_(n=1) ^∞ (1/n) ∫_0 ^1 x^(n+2) ln(x)dx u_n =∫_0 ^1 x^(n+2) ln(x)dx =[(x^(n+3) /(n+3))ln(x)]_0 ^1 −∫_0 ^1 (x^(n+2) /(n+3)) dx =−(1/((n+3)^2 )) ⇒ A =Σ_(n=1) ^∞ (1/(n(n+3)^2 )) let decompose F(x) =(1/(x(x+3)^2 )) ⇒F(x) =(a/x) +(b/(x+3)) +(c/((x+3)^2 )) a=(1/9) , c =−(1/3) ⇒F(x) =(1/(9x)) +(b/(x+3))−(1/(3(x+3)^2 )) lim_(x→+∞) xF(x) =0 =(1/9) +b ⇒b=−(1/9) ⇒ A =lim_(n→+∞) A_n / A_n =Σ_(k=1) ^n (1/(k(k+3)^2 )) =(1/9) Σ_(k=1) ^n (1/k)−(1/9)Σ_(k=1) ^n (1/(k+3))−(1/3) Σ_(k=1) ^n (1/((k+3)^2 )) =(1/9)Σ_(k=1) ^n (1/k)−(1/9) Σ_(k=4) ^(n+3) −(1/3)Σ_(k=4) ^(n+3) (1/k^2 ) =(1/9)(1 +(1/2)+(1/3))−(1/9)((1/(n+1))+(1/(n+2))+(1/(n+3)))−(1/3)(Σ_(k=1) ^(n+3) (1/k^2 )−1−(1/2^2 )−(1/3^2 )) →(1/9)((3/2)+(1/3))−(1/3)×(π^2 /6) +(1/3)(1+(1/4)+(1/9)) =(1/9)(((11)/6))−(π^2 /(18)) +(1/3)((5/4)+(1/9)) =((11)/(54))−(π^2 /(18))+(1/3)(((49)/(36))) =((11)/(54))+((49)/(108))−(π^2 /(18)) ⇒∫_0 ^1 x^2 lnx ln(1−x)dx =((11)/(54))+((49)/(108))−(π^2 /(18))

A = \int_{0}^{1} x^{2} \ln (x) \ln (1 - x) dx we have \frac{d}{dx} \ln (1 - x) = \frac{- 1}{1 - x} = - \sum_{n = 0}^{\infty} x^{n}

\Rightarrow \ln (1 - x) = - \sum_{n = 0}^{\infty} \frac{x^{n + 1}}{n + 1} + c (c = 0) = - \sum_{n = 1}^{\infty} \frac{x^{n}}{n} \Rightarrow

A = - \int_{0}^{1} x^{2} lnx (\sum_{n = 1}^{\infty} \frac{x^{n}}{n}) dx = - \sum_{n = 1}^{\infty} \frac{1}{n} \int_{0}^{1} x^{n + 2} \ln (x) dx

u_{n} = \int_{0}^{1} x^{n + 2} \ln (x) dx = {[\frac{x^{n + 3}}{n + 3} \ln (x)]}_{0}^{1} - \int_{0}^{1} \frac{x^{n + 2}}{n + 3} dx

= - \frac{1}{{(n + 3)}^{2}} \Rightarrow A = \sum_{n = 1}^{\infty} \frac{1}{n {(n + 3)}^{2}} let decompose

F (x) = \frac{1}{x {(x + 3)}^{2}} \Rightarrow F (x) = \frac{a}{x} + \frac{b}{x + 3} + \frac{c}{{(x + 3)}^{2}}

a = \frac{1}{9}, c = - \frac{1}{3} \Rightarrow F (x) = \frac{1}{9 x} + \frac{b}{x + 3} - \frac{1}{3 {(x + 3)}^{2}}

\lim_{x \to + \infty} xF (x) = 0 = \frac{1}{9} + b \Rightarrow b = - \frac{1}{9} \Rightarrow

A = \lim_{n \to + \infty} A_{n} / A_{n} = \sum_{k = 1}^{n} \frac{1}{k {(k + 3)}^{2}}

= \frac{1}{9} \sum_{k = 1}^{n} \frac{1}{k} - \frac{1}{9} \sum_{k = 1}^{n} \frac{1}{k + 3} - \frac{1}{3} \sum_{k = 1}^{n} \frac{1}{{(k + 3)}^{2}}

= \frac{1}{9} \sum_{k = 1}^{n} \frac{1}{k} - \frac{1}{9} \sum_{k = 4}^{n + 3} - \frac{1}{3} \sum_{k = 4}^{n + 3} \frac{1}{k^{2}}

= \frac{1}{9} (1 + \frac{1}{2} + \frac{1}{3}) - \frac{1}{9} (\frac{1}{n + 1} + \frac{1}{n + 2} + \frac{1}{n + 3}) - \frac{1}{3} (\sum_{k = 1}^{n + 3} \frac{1}{k^{2}} - 1 - \frac{1}{2^{2}} - \frac{1}{3^{2}})

\to \frac{1}{9} (\frac{3}{2} + \frac{1}{3}) - \frac{1}{3} \times \frac{π^{2}}{6} + \frac{1}{3} (1 + \frac{1}{4} + \frac{1}{9})

= \frac{1}{9} (\frac{11}{6}) - \frac{π^{2}}{18} + \frac{1}{3} (\frac{5}{4} + \frac{1}{9}) = \frac{11}{54} - \frac{π^{2}}{18} + \frac{1}{3} (\frac{49}{36}) = \frac{11}{54} + \frac{49}{108} - \frac{π^{2}}{18}

\Rightarrow \int_{0}^{1} x^{2} lnx \ln (1 - x) dx = \frac{11}{54} + \frac{49}{108} - \frac{π^{2}}{18}

Commented by mathmax by abdo last updated on 20/Sep/20

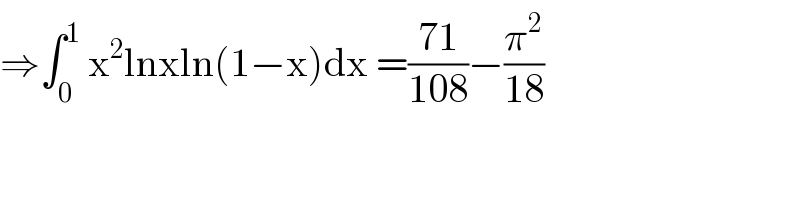
⇒∫_0 ^1 x^2 lnxln(1−x)dx =((71)/(108))−(π^2 /(18))

\Rightarrow \int_{0}^{1} x^{2} lnxln (1 - x) dx = \frac{71}{108} - \frac{π^{2}}{18}

Answered by maths mind last updated on 20/Sep/20

Ψ_1 ((1/4))=∫_0 ^∞ ((ln(x)x^(−(3/4)) )/(x−1))dx x^(1/4) =t⇒dt=((x^(−(3/4)) dx)/4) =∫_0 ^∞ ((4ln(t^4 ))/(t^4 −1))dt =16∫_0 ^1 ((ln(t))/((t^2 −1)(t^2 +1)))dt =8∫_0 ^1 ((ln(t))/(t^2 −1))−∫_0 ^1 ((ln(t))/(t^2 +1)) =−8∫_0 ^1 Σ_(k≥0) t^(2k) ln(t)dt−8Σ_(m≥0) ∫_0 ^1 (−t^2 )^m ln(t)dt =−8Σ_(k≥0) ∫_0 ^1 t^(2k) ln(t)dt−8Σ(−1)^m ∫_0 ^1 t^(2m) ln(t)dt ∫_0 ^1 t^n ln(t)=[((t^(n+1) ln(t))/(n+1))]_0 ^1 −∫(t^n /(n+1))dt=−(1/((n+1)^2 )) =8Σ_(k≥0) (1/((2k+1)^2 ))+8.Σ(((−1)^k )/((2k+1)^2 )) =8.(3/4)ζ(2)+8.G =π^2 +8G

Ψ_{1} (\frac{1}{4}) = \int_{0}^{\infty} \frac{l n (x) x^{- \frac{3}{4}}}{x - 1} d x

x^{\frac{1}{4}} = t \Rightarrow d t = \frac{x^{- \frac{3}{4}} d x}{4}

= \int_{0}^{\infty} \frac{4 l n (t^{4})}{t^{4} - 1} d t

= 16 \int_{0}^{1} \frac{l n (t)}{(t^{2} - 1) (t^{2} + 1)} d t

= 8 \int_{0}^{1} \frac{l n (t)}{t^{2} - 1} - \int_{0}^{1} \frac{l n (t)}{t^{2} + 1}

= - 8 \int_{0}^{1} \sum_{k ⩾ 0} t^{2 k} l n (t) d t - 8 \sum_{m ⩾ 0} \int_{0}^{1} {(- t^{2})}^{m} l n (t) d t

= - 8 \sum_{k ⩾ 0} \int_{0}^{1} t^{2 k} l n (t) d t - 8 Σ {(- 1)}^{m} \int_{0}^{1} t^{2 m} l n (t) d t

\int_{0}^{1} t^{n} l n (t) = {[\frac{t^{n + 1} l n (t)}{n + 1}]}_{0}^{1} - \int \frac{t^{n}}{n + 1} d t = - \frac{1}{{(n + 1)}^{2}}

= 8 \sum_{k ⩾ 0} \frac{1}{{(2 k + 1)}^{2}} + 8 . Σ \frac{{(- 1)}^{k}}{{(2 k + 1)}^{2}}

= 8 . \frac{3}{4} ζ (2) + 8 . G

= π^{2} + 8 G

Facebook Tweet Pin

calculus-evaluate-i-0-1-t-2-ln-t-ln-1-t-dt-ii-1-4-iii-0-pi-8-ln-tan-x-dx-

Leave a Reply Cancel reply