Question Number 147262 by mnjuly1970 last updated on 19/Jul/21
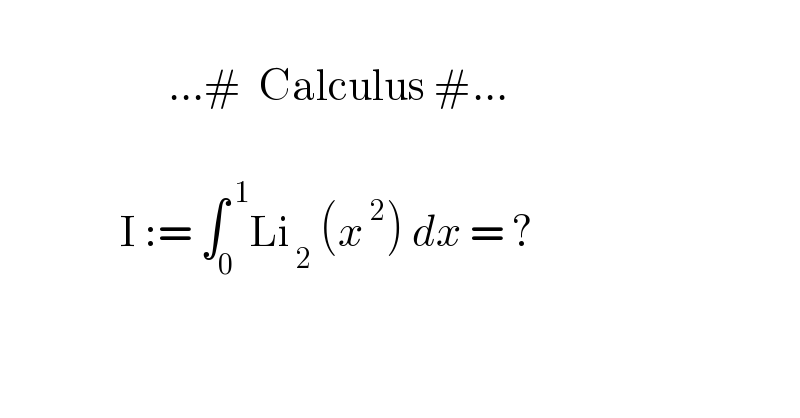
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…#\:\:\mathrm{Calculus}\:#… \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{I}\::=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{Li}_{\:\mathrm{2}} \:\left({x}^{\:\mathrm{2}} \right)\:{dx}\:=\:? \\ $$$$ \\ $$$$ \\ $$
Answered by qaz last updated on 19/Jul/21
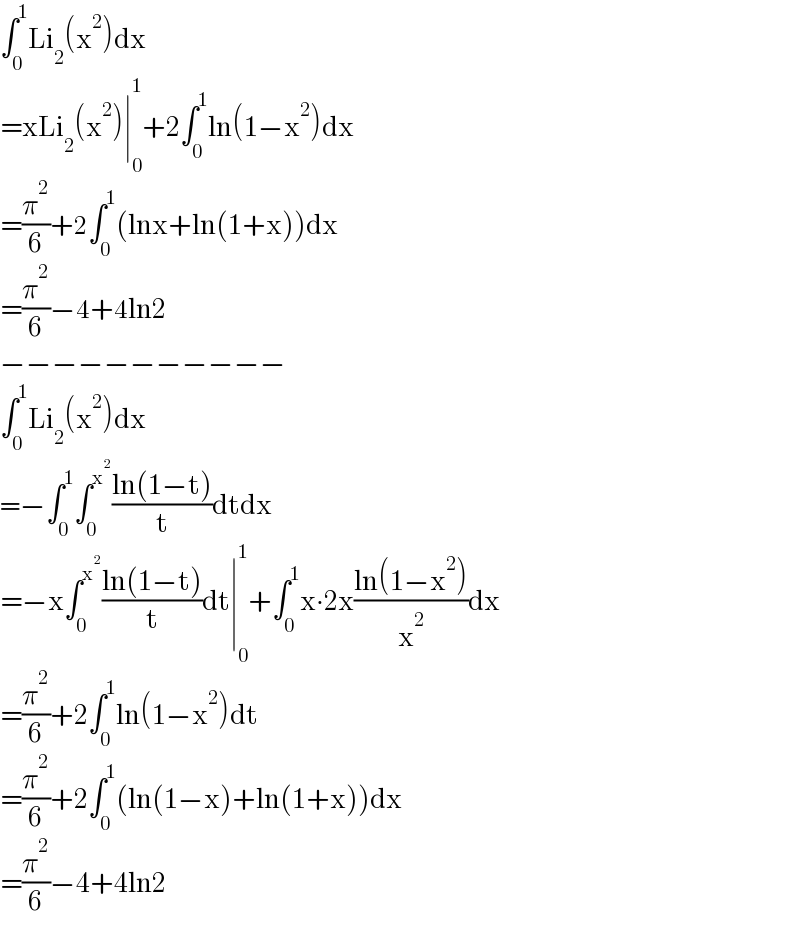
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$=\mathrm{xLi}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \right)\mid_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{lnx}+\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{4}+\mathrm{4ln2} \\ $$$$−−−−−−−−−−− \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)}{\mathrm{t}}\mathrm{dtdx} \\ $$$$=−\mathrm{x}\int_{\mathrm{0}} ^{\mathrm{x}^{\mathrm{2}} } \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)}{\mathrm{t}}\mathrm{dt}\mid_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}\centerdot\mathrm{2x}\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{dt} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)+\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{4}+\mathrm{4ln2} \\ $$
Commented by mnjuly1970 last updated on 19/Jul/21
$$\:\:{thanks}\:{alot}\:{sir}\:{qaz}…{very}\:{nice}… \\ $$
Answered by Olaf_Thorendsen last updated on 19/Jul/21
![I = ∫_0 ^1 Li_2 (x^2 )dx I = ∫_0 ^( 1) Σ_(k=1) ^∞ (((x^2 )^k )/k^2 ) dx I = ∫_0 ^( 1) Σ_(k=1) ^∞ (x^(2k) /k^2 ) dx I = [Σ_(k=1) ^∞ (x^(2k+1) /(k^2 (2k+1)))]_0 ^1 I = Σ_(k=1) ^∞ (1/(k^2 (2k+1))) I = (1/2)Σ_(k=1) ^∞ (1/(k^2 (k+(1/2)))) I = Σ_(k=1) ^∞ ((1/k^2 )−(1/(k(k+(1/2))))) I = Σ_(k=1) ^∞ (1/k^2 )−Σ_(k=0) ^∞ (1/((k+1)(k+(3/2)))) I = (π^2 /6)−((ψ((3/2))−ψ(1))/((3/2)−1)) ψ(1) = −γ and ψ((1/2)) = −2ln2−γ ψ(z+1) = ψ(z)+(1/z) ⇒ ψ((3/2)) = ψ((1/2))+2 = −2ln2−γ+2 I = (π^2 /6)−((−2ln2−γ+2+γ)/(1/2)) I = (π^2 /6)+4ln2−4](https://www.tinkutara.com/question/Q147265.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{Li}_{\mathrm{2}} \left({x}^{\mathrm{2}} \right){dx} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({x}^{\mathrm{2}} \right)^{{k}} }{{k}^{\mathrm{2}} }\:\mathrm{d}{x} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{k}} }{{k}^{\mathrm{2}} }\:\mathrm{d}{x} \\ $$$$\mathrm{I}\:=\:\left[\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{k}+\mathrm{1}} }{{k}^{\mathrm{2}} \left(\mathrm{2}{k}+\mathrm{1}\right)}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left(\mathrm{2}{k}+\mathrm{1}\right)} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} \left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$\mathrm{I}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{{k}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\right) \\ $$$$\mathrm{I}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)\left({k}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$\mathrm{I}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\psi\left(\mathrm{1}\right)}{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} \\ $$$$\psi\left(\mathrm{1}\right)\:=\:−\gamma\:\mathrm{and}\:\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:−\mathrm{2ln2}−\gamma \\ $$$$\psi\left({z}+\mathrm{1}\right)\:=\:\psi\left({z}\right)+\frac{\mathrm{1}}{{z}} \\ $$$$\Rightarrow\:\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\:\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}\:=\:−\mathrm{2ln2}−\gamma+\mathrm{2} \\ $$$$\mathrm{I}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\frac{−\mathrm{2ln2}−\gamma+\mathrm{2}+\gamma}{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{I}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\mathrm{4ln2}−\mathrm{4} \\ $$
Commented by mnjuly1970 last updated on 19/Jul/21
$$\:\:\:{grateful}\:{sir}\:{olaf}..{excellent}… \\ $$
