Menu Close

calculus-I-complex-analysis-calculate-0-ln-x-x-2-3x-2-dx-ln-2-2-2-

Tinku Tara 0 Comments
Pin




Question Number 127224 by mnjuly1970 last updated on 28/Dec/20
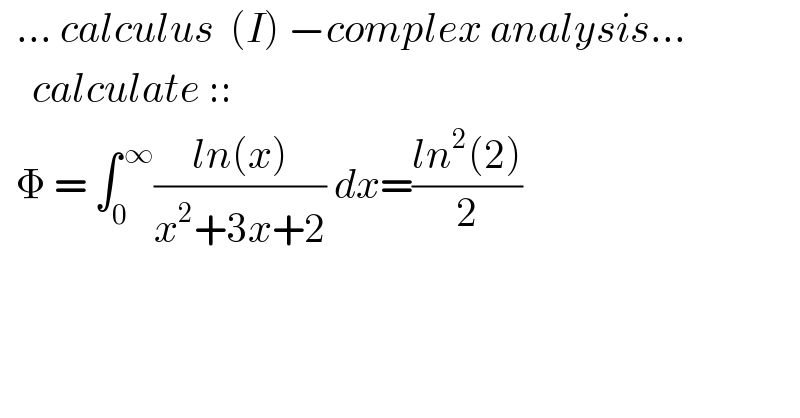
... calculus (I) −complex analysis... calculate :: Φ = ∫_0 ^( ∞) ((ln(x))/(x^2 +3x+2)) dx=((ln^2 (2))/2)
$$\:\:…\:{calculus}\:\:\left({I}\right)\:−{complex}\:{analysis}… \\ $$$$\:\:\:\:{calculate}\:::\: \\ $$$$\:\:\Phi\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{2}}\:{dx}=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Answered by mindispower last updated on 27/Dec/20
f(z)=((ln(z))/(z^2 +2z+3)),a=−1−i(√2) ∫_0 ^∞ ((ln^2 (z))/(z^2 +2z+3))−∫_0 ^∞ (((ln(z)+2iπ)^2 )/(z^2 +2z+3))dz=2iπRes(f(z),a,a^− ) =−4iπ∫_0 ^∞ ((ln(z))/(z^2 +2z+3))+∫_0 ^∞ ((4π^2 dz)/(z^2 +2z+3))=2iπRes(f,a^− ,a) ⇒∫_0 ^∞ ((ln(z))/(z^2 +2z+3))dz=−(1/2)Re(Res(f,a,a^− )) Res(f,a,a^− )=((ln(a))/(2a+2))+((ln(a^− ))/(2a^− +2)) ln(−1−i(√2))=ln((√3))+i(arctan((√2))+π) ln(−1+i(√2))=ln((√3))+i(π−arctan((√2))) =(((ln((√3))+i(π+arctan((√2)))^2 )/(−2i(√2)))+(((ln((√3))+i(π−arctan((√2))))^2 )/(2i(√2))) =2((−iln((√3))arctan((√2))+πarctan((√2)))/(i(√2))) ∫_0 ^∞ ((ln(x))/(x^2 +2x+3))dx=((ln((√3))arctan((√2)))/( (√2)))≃0,371
$${f}\left({z}\right)=\frac{{ln}\left({z}\right)}{{z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{3}},{a}=−\mathrm{1}−{i}\sqrt{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{{z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{3}}−\int_{\mathrm{0}} ^{\infty} \frac{\left({ln}\left({z}\right)+\mathrm{2}{i}\pi\right)^{\mathrm{2}} }{{z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{3}}{dz}=\mathrm{2}{i}\pi{Res}\left({f}\left({z}\right),{a},\overset{−} {{a}}\right) \\ $$$$=−\mathrm{4}{i}\pi\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left({z}\right)}{{z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{3}}+\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{4}\pi^{\mathrm{2}} {dz}}{{z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{3}}=\mathrm{2}{i}\pi{Res}\left({f},\overset{−} {{a}},{a}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left({z}\right)}{{z}^{\mathrm{2}} +\mathrm{2}{z}+\mathrm{3}}{dz}=−\frac{\mathrm{1}}{\mathrm{2}}{Re}\left({Res}\left({f},{a},\overset{−} {{a}}\right)\right) \\ $$$${Res}\left({f},{a},\overset{−} {{a}}\right)=\frac{{ln}\left({a}\right)}{\mathrm{2}{a}+\mathrm{2}}+\frac{{ln}\left(\overset{−} {{a}}\right)}{\mathrm{2}\overset{−} {{a}}+\mathrm{2}} \\ $$$${ln}\left(−\mathrm{1}−{i}\sqrt{\mathrm{2}}\right)={ln}\left(\sqrt{\mathrm{3}}\right)+{i}\left({arctan}\left(\sqrt{\mathrm{2}}\right)+\pi\right) \\ $$$${ln}\left(−\mathrm{1}+{i}\sqrt{\mathrm{2}}\right)={ln}\left(\sqrt{\mathrm{3}}\right)+{i}\left(\pi−{arctan}\left(\sqrt{\mathrm{2}}\right)\right) \\ $$$$=\frac{\left({ln}\left(\sqrt{\mathrm{3}}\right)+{i}\left(\pi+{arctan}\left(\sqrt{\mathrm{2}}\right)\right)^{\mathrm{2}} \right.}{−\mathrm{2}{i}\sqrt{\mathrm{2}}}+\frac{\left({ln}\left(\sqrt{\mathrm{3}}\right)+{i}\left(\pi−{arctan}\left(\sqrt{\mathrm{2}}\right)\right)\right)^{\mathrm{2}} }{\mathrm{2}{i}\sqrt{\mathrm{2}}} \\ $$$$=\mathrm{2}\frac{−{iln}\left(\sqrt{\mathrm{3}}\right){arctan}\left(\sqrt{\mathrm{2}}\right)+\pi{arctan}\left(\sqrt{\mathrm{2}}\right)}{{i}\sqrt{\mathrm{2}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left({x}\right)}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}}{dx}=\frac{{ln}\left(\sqrt{\mathrm{3}}\right){arctan}\left(\sqrt{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}}\simeq\mathrm{0},\mathrm{371} \\ $$
Commented by mnjuly1970 last updated on 28/Dec/20
thank you so much ..
$${thank}\:{you}\:{so}\:{much}\:.. \\ $$$$\: \\ $$
Commented by mindispower last updated on 28/Dec/20
always pleasur
$${always}\:{pleasur} \\ $$
Answered by Bird last updated on 28/Dec/20
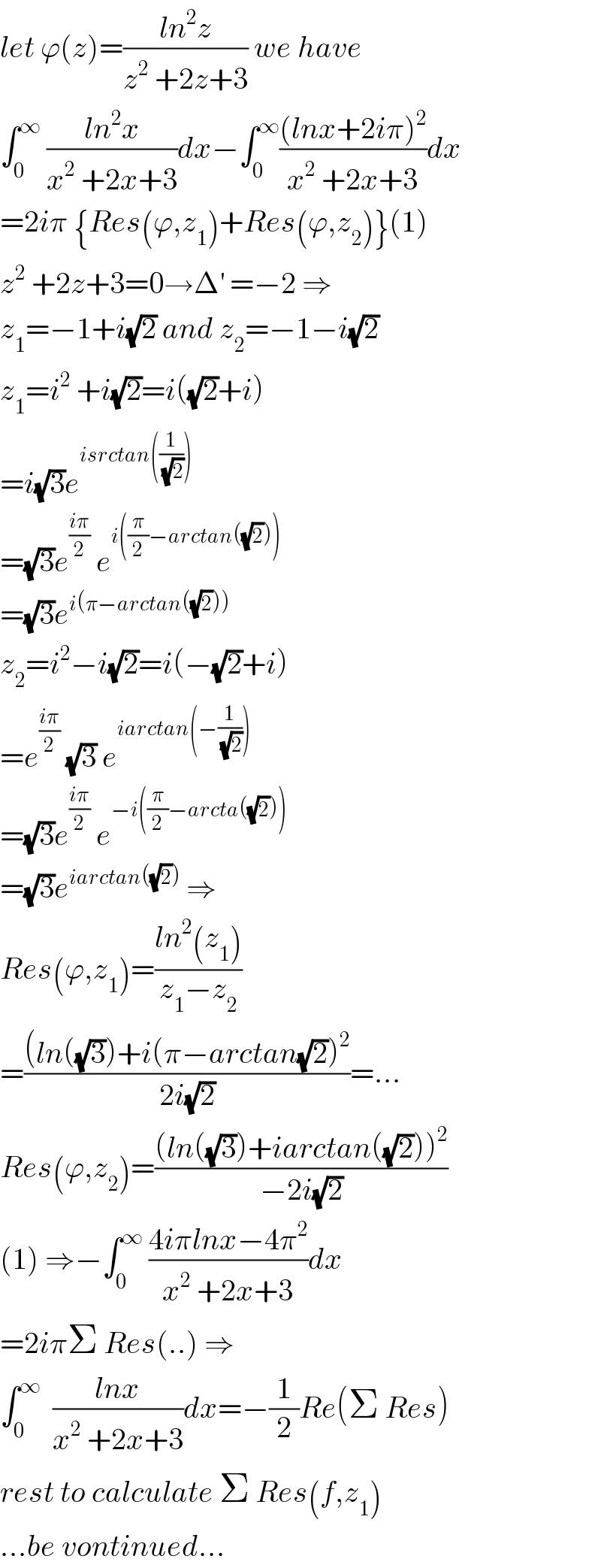
let ϕ(z)=((ln^2 z)/(z^2 +2z+3)) we have ∫_0 ^∞ ((ln^2 x)/(x^2 +2x+3))dx−∫_0 ^∞ (((lnx+2iπ)^2 )/(x^2 +2x+3))dx =2iπ {Res(ϕ,z_1 )+Res(ϕ,z_2 )}(1) z^2 +2z+3=0→Δ^′ =−2 ⇒ z_1 =−1+i(√2) and z_2 =−1−i(√2) z_1 =i^2 +i(√2)=i((√2)+i) =i(√3)e^(isrctan((1/( (√2))))) =(√3)e^((iπ)/2) e^(i((π/2)−arctan((√2)))) =(√3)e^(i(π−arctan((√2)))) z_2 =i^2 −i(√2)=i(−(√2)+i) =e^((iπ)/2) (√3) e^(iarctan(−(1/( (√2))))) =(√3)e^((iπ)/2) e^(−i((π/2)−arcta((√2)))) =(√3)e^(iarctan((√2))) ⇒ Res(ϕ,z_1 )=((ln^2 (z_1 ))/(z_1 −z_2 )) =(((ln((√3))+i(π−arctan(√2))^2 )/(2i(√2)))=... Res(ϕ,z_2 )=(((ln((√3))+iarctan((√2)))^2 )/(−2i(√2))) (1) ⇒−∫_0 ^∞ ((4iπlnx−4π^2 )/(x^2 +2x+3))dx =2iπΣ Res(..) ⇒ ∫_0 ^∞ ((lnx)/(x^2 +2x+3))dx=−(1/2)Re(Σ Res) rest to calculate Σ Res(f,z_1 ) ...be vontinued...
$${let}\:\varphi\left({z}\right)=\frac{{ln}^{\mathrm{2}} {z}}{{z}^{\mathrm{2}} \:+\mathrm{2}{z}+\mathrm{3}}\:{we}\:{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{ln}^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}{dx}−\int_{\mathrm{0}} ^{\infty} \frac{\left({lnx}+\mathrm{2}{i}\pi\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}{dx}\: \\ $$$$=\mathrm{2}{i}\pi\:\left\{{Res}\left(\varphi,{z}_{\mathrm{1}} \right)+{Res}\left(\varphi,{z}_{\mathrm{2}} \right)\right\}\left(\mathrm{1}\right) \\ $$$${z}^{\mathrm{2}} \:+\mathrm{2}{z}+\mathrm{3}=\mathrm{0}\rightarrow\Delta^{'} \:=−\mathrm{2}\:\Rightarrow \\ $$$${z}_{\mathrm{1}} =−\mathrm{1}+{i}\sqrt{\mathrm{2}}\:{and}\:{z}_{\mathrm{2}} =−\mathrm{1}−{i}\sqrt{\mathrm{2}} \\ $$$${z}_{\mathrm{1}} ={i}^{\mathrm{2}} \:+{i}\sqrt{\mathrm{2}}={i}\left(\sqrt{\mathrm{2}}+{i}\right) \\ $$$$={i}\sqrt{\mathrm{3}}{e}^{{isrctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)} \\ $$$$=\sqrt{\mathrm{3}}{e}^{\frac{{i}\pi}{\mathrm{2}}} \:{e}^{{i}\left(\frac{\pi}{\mathrm{2}}−{arctan}\left(\sqrt{\mathrm{2}}\right)\right)} \\ $$$$=\sqrt{\mathrm{3}}{e}^{{i}\left(\pi−{arctan}\left(\sqrt{\mathrm{2}}\right)\right)} \\ $$$${z}_{\mathrm{2}} ={i}^{\mathrm{2}} −{i}\sqrt{\mathrm{2}}={i}\left(−\sqrt{\mathrm{2}}+{i}\right) \\ $$$$={e}^{\frac{{i}\pi}{\mathrm{2}}} \:\sqrt{\mathrm{3}}\:{e}^{{iarctan}\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)} \\ $$$$=\sqrt{\mathrm{3}}{e}^{\frac{{i}\pi}{\mathrm{2}}} \:{e}^{−{i}\left(\frac{\pi}{\mathrm{2}}−{arcta}\left(\sqrt{\mathrm{2}}\right)\right)} \\ $$$$=\sqrt{\mathrm{3}}{e}^{{iarctan}\left(\sqrt{\mathrm{2}}\right)} \:\Rightarrow \\ $$$${Res}\left(\varphi,{z}_{\mathrm{1}} \right)=\frac{{ln}^{\mathrm{2}} \left({z}_{\mathrm{1}} \right)}{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} } \\ $$$$=\frac{\left({ln}\left(\sqrt{\mathrm{3}}\right)+{i}\left(\pi−{arctan}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \right.}{\mathrm{2}{i}\sqrt{\mathrm{2}}}=… \\ $$$${Res}\left(\varphi,{z}_{\mathrm{2}} \right)=\frac{\left({ln}\left(\sqrt{\mathrm{3}}\right)+{iarctan}\left(\sqrt{\mathrm{2}}\right)\right)^{\mathrm{2}} }{−\mathrm{2}{i}\sqrt{\mathrm{2}}} \\ $$$$\left(\mathrm{1}\right)\:\Rightarrow−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{4}{i}\pi{lnx}−\mathrm{4}\pi^{\mathrm{2}} }{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}{dx} \\ $$$$=\mathrm{2}{i}\pi\Sigma\:{Res}\left(..\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{{x}^{\mathrm{2}} \:+\mathrm{2}{x}+\mathrm{3}}{dx}=−\frac{\mathrm{1}}{\mathrm{2}}{Re}\left(\Sigma\:{Res}\right) \\ $$$${rest}\:{to}\:{calculate}\:\Sigma\:{Res}\left({f},{z}_{\mathrm{1}} \right) \\ $$$$…{be}\:{vontinued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *