Question Number 126766 by mnjuly1970 last updated on 24/Dec/20
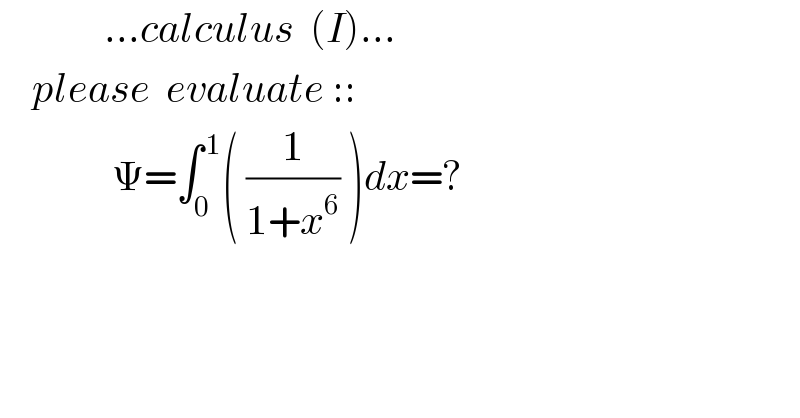
$$\:\:\:\:\:\:\:\:\:\:\:\:\:…{calculus}\:\:\left({I}\right)… \\ $$$$\:\:\:\:{please}\:\:{evaluate}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Psi=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{6}} }\:\right){dx}=? \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 24/Dec/20
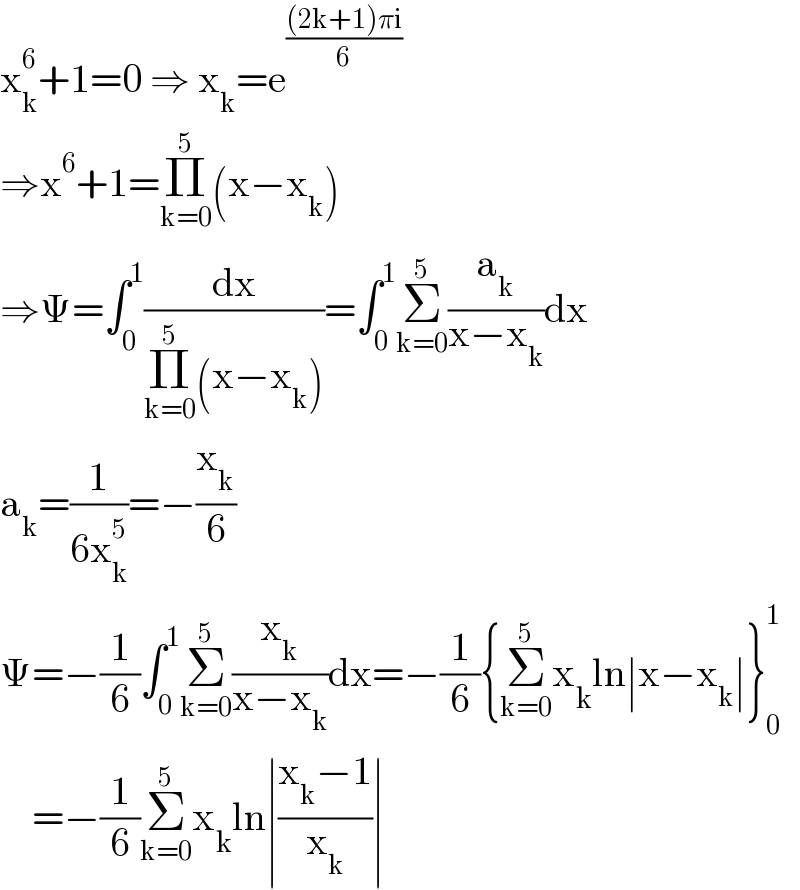
$$\mathrm{x}_{\mathrm{k}} ^{\mathrm{6}} +\mathrm{1}=\mathrm{0}\:\Rightarrow\:\mathrm{x}_{\mathrm{k}} =\mathrm{e}^{\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi\mathrm{i}}{\mathrm{6}}} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{6}} +\mathrm{1}=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{5}} {\prod}}\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right) \\ $$$$\Rightarrow\Psi=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{5}} {\prod}}\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)}=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{x}−\mathrm{x}_{\mathrm{k}} }\mathrm{dx} \\ $$$$\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{1}}{\mathrm{6x}_{\mathrm{k}} ^{\mathrm{5}} }=−\frac{\mathrm{x}_{\mathrm{k}} }{\mathrm{6}} \\ $$$$\Psi=−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\frac{\mathrm{x}_{\mathrm{k}} }{\mathrm{x}−\mathrm{x}_{\mathrm{k}} }\mathrm{dx}=−\frac{\mathrm{1}}{\mathrm{6}}\left\{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\mathrm{x}_{\mathrm{k}} \mathrm{ln}\mid\mathrm{x}−\mathrm{x}_{\mathrm{k}} \mid\right\}_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:=−\frac{\mathrm{1}}{\mathrm{6}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\mathrm{x}_{\mathrm{k}} \mathrm{ln}\mid\frac{\mathrm{x}_{\mathrm{k}} −\mathrm{1}}{\mathrm{x}_{\mathrm{k}} }\mid \\ $$
Commented by mnjuly1970 last updated on 24/Dec/20
$${thank}\:{you}\:{so}\:{much}\:{sir}\:{brandon}.. \\ $$
Answered by mindispower last updated on 24/Dec/20
![=∫_0 ^1 ((1−x^6 )/(1−x^(12_ ) )) =(1/(12))∫_0 ^1 ((1−t^(1/2) )/(1−t)).t^(−((11)/(12))) =(1/(12))(−γ+∫_0 ^1 ((t^(−((11)/(12))) −1)/(1−t))dt)−(1/(12))(−γ+∫_0 ^1 ((1−t^((−5)/(12)) )/(1−t))dt) =((Ψ((1/(12)))−Ψ((7/(12))))/(12)). we have close for Ψ((p/q))=−γ−ln(2q)−(π/2)cot(((pπ)/q)) +2Σ_1 ^([((q−1)/2)]) cos(((2πnp)/q))ln(sin(((πn)/q)))](https://www.tinkutara.com/question/Q126772.png)
$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{6}} }{\mathrm{1}−{x}^{\mathrm{12}_{} } \:\:} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{t}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}−{t}}.{t}^{−\frac{\mathrm{11}}{\mathrm{12}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left(−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{−\frac{\mathrm{11}}{\mathrm{12}}} −\mathrm{1}}{\mathrm{1}−{t}}{dt}\right)−\frac{\mathrm{1}}{\mathrm{12}}\left(−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{t}^{\frac{−\mathrm{5}}{\mathrm{12}}} }{\mathrm{1}−{t}}{dt}\right) \\ $$$$=\frac{\Psi\left(\frac{\mathrm{1}}{\mathrm{12}}\right)−\Psi\left(\frac{\mathrm{7}}{\mathrm{12}}\right)}{\mathrm{12}}.\: \\ $$$${we}\:{have}\:{close}\:{for}\:\Psi\left(\frac{{p}}{{q}}\right)=−\gamma−{ln}\left(\mathrm{2}{q}\right)−\frac{\pi}{\mathrm{2}}{cot}\left(\frac{{p}\pi}{{q}}\right) \\ $$$$+\mathrm{2}\underset{\mathrm{1}} {\overset{\left[\frac{{q}−\mathrm{1}}{\mathrm{2}}\right]} {\sum}}{cos}\left(\frac{\mathrm{2}\pi{np}}{{q}}\right){ln}\left({sin}\left(\frac{\pi{n}}{{q}}\right)\right) \\ $$
Commented by mnjuly1970 last updated on 24/Dec/20

$${grateful}..{peace}\:{be}\:{upon}\:{you} \\ $$$${sir}\:\:{minds}.. \\ $$
Answered by MJS_new last updated on 24/Dec/20
![Ψ=∫_0 ^1 (dx/(x^6 +1))=[Σ_(j=1) ^5 I_j ]_0 ^1 I_1 =(1/3)∫_0 ^1 (dx/(x^2 +1))=(1/3)[arctan x]_0 ^1 =(π/(12)) I_2 =(1/(12))∫_0 ^1 (dx/(x^2 +(√3)x+1))=(1/6)[arctan (2x+(√3))]_0 ^1 =(π/(72)) I_3 =((√3)/(12))∫((2x+(√3))/(x^2 +(√3)x+1))=((√3)/(12))[ln (x^2 +(√3)x+1)]_0 ^1 =((√3)/(12))ln (2+(√3)) I_4 =(1/(12))∫(dx/(x^2 −(√3)x+1))=(1/6)[arctan (2x−(√3))]_0 ^1 =((5π)/(72)) I_5 =−((√3)/(12))∫((2x−3)/(x^2 −(√3)x+1))=−((√3)/(12))[ln (x^2 −(√3)x+1)]_0 ^1 =−((√3)/(12))ln (2−(√3)) ⇒ Ψ=(π/6)+((√3)/6)ln (2+(√3))](https://www.tinkutara.com/question/Q126787.png)
$$\Psi=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{{x}^{\mathrm{6}} +\mathrm{1}}=\left[\underset{{j}=\mathrm{1}} {\overset{\mathrm{5}} {\sum}}{I}_{{j}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{arctan}\:{x}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi}{\mathrm{12}} \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{12}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{arctan}\:\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi}{\mathrm{72}} \\ $$$${I}_{\mathrm{3}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\int\frac{\mathrm{2}{x}+\sqrt{\mathrm{3}}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\left[\mathrm{ln}\:\left({x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$${I}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{12}}\int\frac{{dx}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{6}}\left[\mathrm{arctan}\:\left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{5}\pi}{\mathrm{72}} \\ $$$${I}_{\mathrm{5}} =−\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\int\frac{\mathrm{2}{x}−\mathrm{3}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}=−\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\left[\mathrm{ln}\:\left({x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =−\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\mathrm{ln}\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow \\ $$$$\Psi=\frac{\pi}{\mathrm{6}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$
Commented by mnjuly1970 last updated on 24/Dec/20
$${thanks}\:{alot}\:{mr}\:\:{mjs}.. \\ $$
Answered by mnjuly1970 last updated on 24/Dec/20
![Ψ=(1/2)∫_0 ^( 1() ((1+x^4 −x^2 )+x^2 +(1−x^4 ))/(1+x^6 ))dx Ψ=(1/2)[∫_0 ^( 1) (1/(1+x^2 ))dx=Ω_1 ]+(1/2)[∫_0 ^( 1) (x^2 /(1+(x^3 )^2 ))dx=Ω_2 ] +(1/2)[∫_0 ^( 1) ((1−x^2 )/(1−x^2 +x^4 ))dx=Ω_3 ] ∴ Ω_1 =(π/4) Ω_2 =^(x^3 =t) (1/3)∫_0 ^( 1) (1/(1+t^2 ))dt=(π/(12)) Ω_3 =−∫((1−x^(−2) )/(x^2 −1+x^(−2) ))dx=−∫_0 ^( 1) ((1−x^(−2) )/((x+x^(−1) )^2 −3))dx =^(x+x^(−1) =t) −∫_∞ ^( 2) (dt/(t^2 −3))=(1/(2(√3)))∫_2 ^( ∞) (1/(t−(√3))) −(1/(t+(√3))) =(1/(2(√3))) ln(((t−(√3))/(t+(√3))))_(2 ) ^∞ =−(1/(2(√3)))ln(((2−(√3))/(2+(√3)))) ✓ Ψ=(π/8)+(π/(24))−(1/(4(√3))) ln(((2−(√3))/(2+(√3))))=(π/6)+(1/(4(√3))) ln(((2+(√3))/(2−(√3))))✓ =(π/6)+(1/(2(√3)))ln(2+(√3) )✓](https://www.tinkutara.com/question/Q126831.png)
$$\:\Psi=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}\left(\right.} \frac{\left.\mathrm{1}+{x}^{\mathrm{4}} −{x}^{\mathrm{2}} \right)+{x}^{\mathrm{2}} +\left(\mathrm{1}−{x}^{\mathrm{4}} \right)}{\mathrm{1}+{x}^{\mathrm{6}} }{dx} \\ $$$$\:\Psi=\frac{\mathrm{1}}{\mathrm{2}}\left[\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\Omega_{\mathrm{1}} \right]+\frac{\mathrm{1}}{\mathrm{2}}\left[\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{1}+\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx}=\Omega_{\mathrm{2}} \right] \\ $$$$\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}\left[\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}=\Omega_{\mathrm{3}} \right] \\ $$$$\:\:\therefore\:\Omega_{\mathrm{1}} =\frac{\pi}{\mathrm{4}}\:\: \\ $$$$\:\:\:\:\:\Omega_{\mathrm{2}} \overset{{x}^{\mathrm{3}} ={t}} {=}\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\frac{\pi}{\mathrm{12}} \\ $$$$\:\:\:\:\:\Omega_{\mathrm{3}} =−\int\frac{\mathrm{1}−{x}^{−\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{1}+{x}^{−\mathrm{2}} }{dx}=−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{x}^{−\mathrm{2}} }{\left({x}+{x}^{−\mathrm{1}} \right)^{\mathrm{2}} −\mathrm{3}}{dx} \\ $$$$\overset{{x}+{x}^{−\mathrm{1}} ={t}} {=}\:−\int_{\infty} ^{\:\mathrm{2}} \frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\int_{\mathrm{2}} ^{\:\infty} \frac{\mathrm{1}}{{t}−\sqrt{\mathrm{3}}}\:−\frac{\mathrm{1}}{{t}+\sqrt{\mathrm{3}}} \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\:{ln}\left(\frac{{t}−\sqrt{\mathrm{3}}}{{t}+\sqrt{\mathrm{3}}}\right)_{\mathrm{2}\:} ^{\infty} =−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{3}}}\right)\:\checkmark \\ $$$$\:\:\:\Psi=\frac{\pi}{\mathrm{8}}+\frac{\pi}{\mathrm{24}}−\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\:{ln}\left(\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{3}}}\right)=\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}\:{ln}\left(\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}−\sqrt{\mathrm{3}}}\right)\checkmark\:\: \\ $$$$=\frac{\pi}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)\checkmark \\ $$$$ \\ $$
