Question Number 112579 by mnjuly1970 last updated on 08/Sep/20
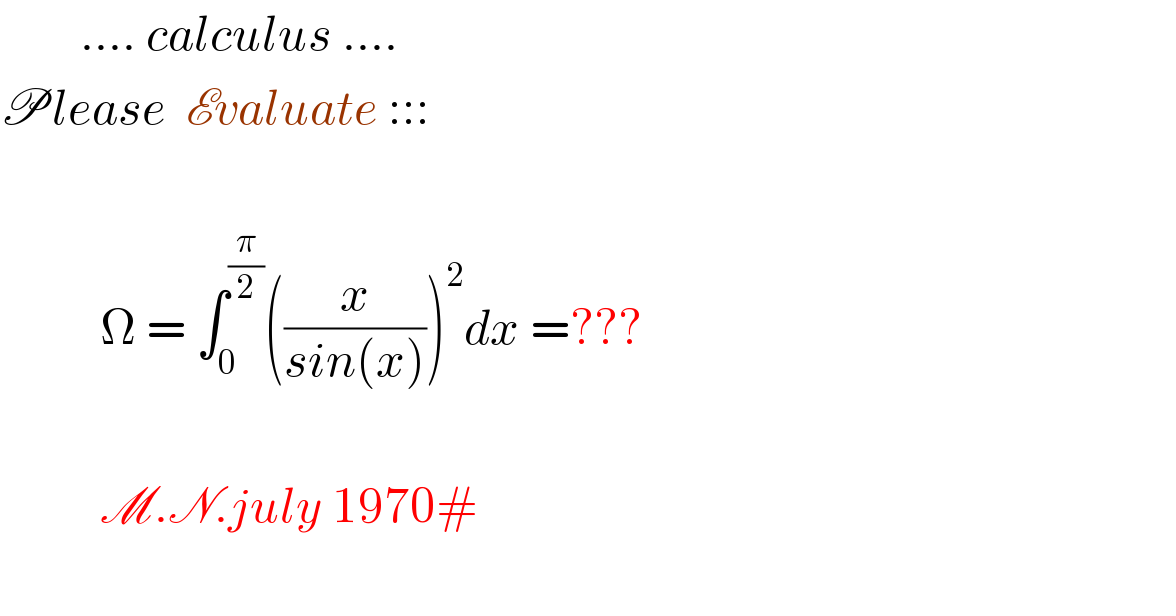
$$\:\:\:\:\:\:\:\:….\:{calculus}\:…. \\ $$$$\mathscr{P}{lease}\:\:\mathscr{E}{valuate}\:::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{{x}}{{sin}\left({x}\right)}\right)^{\mathrm{2}} {dx}\:=???\:\:\:\:\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathscr{M}.\mathscr{N}.{july}\:\mathrm{1970}# \\ $$$$\: \\ $$
Answered by mathmax by abdo last updated on 09/Sep/20
![Ω =∫_0 ^(π/2) (x^2 /(sin^2 x))dx ⇒Ω =∫_0 ^(π/2) (x^2 /(1−cos^2 x)) dx we do the changement tanx =t ⇒x =arctan(t) ⇒Ω =∫_0 ^∞ ((arctan^2 t)/(1−(1/(1+t^2 ))))×(dt/(1+t^2 )) =∫_0 ^∞ ((arctan^2 t)/(1+t^2 −1))dt =∫_0 ^∞ ((arctan^2 t)/t^2 ) dt by parts ∫_0 ^∞ ((arctan^2 t)/t^2 )dt =[−((arctan^2 t)/t)]_0 ^∞ +∫_0 ^∞ (1/t)×((2arctant)/((1+t^2 )))dt =2 ∫_0 ^∞ ((arctan(t))/(t(1+t^2 ))) dt =∫_(−∞) ^(+∞) ((arctant)/(t(t^2 +1)))dt let ϕ(z) =((arctanz)/(z(z^2 +1))) ⇒ϕ(z) =((arctan(z))/(z(z−i)(z+i))) residus theorem give ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,o)+Res(ϕ ,i)} Res(ϕ,o) =lim_(z→0) zϕ(z) =lim_(z→0) ((arctanz)/(z^2 +1)) =0 Res(ϕ,i) =lim_(z→i) (z−i)ϕ(z) =((arctan(i))/(i(2i))) =−(1/2) arctan(i) ⇒∫_(−∞) ^(+∞) ϕ(z)dz =2iπ×(−(1/2) arctan(i)} =−iπ arctan(i) ⇒ Ω =−iπ arctan(i) rest to find arctan(i) ...be continued we have the formula arctanz =(1/(2i))ln(((1+iz)/(1−iz))) but this is not applicable for i.....be continued....](https://www.tinkutara.com/question/Q112627.png)
$$\Omega\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:\Rightarrow\Omega\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\:\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement} \\ $$$$\mathrm{tanx}\:=\mathrm{t}\:\Rightarrow\mathrm{x}\:=\mathrm{arctan}\left(\mathrm{t}\right)\:\Rightarrow\Omega\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctan}^{\mathrm{2}} \mathrm{t}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}×\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{arctan}^{\mathrm{2}} \mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctan}^{\mathrm{2}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}\:\:\mathrm{by}\:\mathrm{parts} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctan}^{\mathrm{2}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\left[−\frac{\mathrm{arctan}^{\mathrm{2}} \mathrm{t}}{\mathrm{t}}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{t}}×\frac{\mathrm{2arctant}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{arctan}\left(\mathrm{t}\right)}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:\mathrm{dt}\:\:=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{arctant}}{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)}\mathrm{dt}\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{arctanz}}{\mathrm{z}\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$\Rightarrow\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{arctan}\left(\mathrm{z}\right)}{\mathrm{z}\left(\mathrm{z}−\mathrm{i}\right)\left(\mathrm{z}+\mathrm{i}\right)}\:\mathrm{residus}\:\mathrm{theorem}\:\mathrm{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\:\mathrm{Res}\left(\varphi,\mathrm{o}\right)+\mathrm{Res}\left(\varphi\:,\mathrm{i}\right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{o}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \:\:\mathrm{z}\varphi\left(\mathrm{z}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{arctanz}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}}\:=\mathrm{0} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{i}\right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\left(\mathrm{z}−\mathrm{i}\right)\varphi\left(\mathrm{z}\right)\:=\frac{\mathrm{arctan}\left(\mathrm{i}\right)}{\mathrm{i}\left(\mathrm{2i}\right)}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{arctan}\left(\mathrm{i}\right) \\ $$$$\Rightarrow\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi×\left(−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{arctan}\left(\mathrm{i}\right)\right\} \\ $$$$=−\mathrm{i}\pi\:\mathrm{arctan}\left(\mathrm{i}\right)\:\Rightarrow\:\Omega\:=−\mathrm{i}\pi\:\mathrm{arctan}\left(\mathrm{i}\right)\:\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{arctan}\left(\mathrm{i}\right) \\ $$$$…\mathrm{be}\:\mathrm{continued} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{arctanz}\:=\frac{\mathrm{1}}{\mathrm{2i}}\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{iz}}{\mathrm{1}−\mathrm{iz}}\right)\:\mathrm{but}\:\mathrm{this}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{applicable}\:\mathrm{for}\:\mathrm{i}…..\mathrm{be}\:\mathrm{continued}…. \\ $$
Commented by mnjuly1970 last updated on 09/Sep/20
$${grateful}\:{sir}\:{mathmax}.{god}\: \\ $$$${keep}\:\:{you}.. \\ $$
Commented by mathmax by abdo last updated on 10/Sep/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mathdave last updated on 09/Sep/20
![my solution to I=∫_0 ^(π/2) ((x/(sinx)))^2 dx (using IBP) I=[−((x^2 cosx)/(sinx))]_0 ^(π/2) +2∫_0 ^(π/2) xcotxdx (using IBP) I=0+2[xln(sinx)]_0 ^((.π)/2) −2∫_0 ^(π/2) ln(sinx)dx I=0+0−2∫_0 ^(π/2) ln(sinx)dx but ∫_0 ^(π/2) ln(sinx)dx=−(π/2)ln2 ∵I=−2[−(π/2)ln2]=πln2 ∵∫_0 ^(π/2) ((x/(sinx)))^2 dx=πln2 by mathdave(08/09/2020)](https://www.tinkutara.com/question/Q112635.png)
$${my}\:{solution}\:{to}\: \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{{x}}{\mathrm{sin}{x}}\right)^{\mathrm{2}} {dx}\:\:\:\left({using}\:{IBP}\right) \\ $$$${I}=\left[−\frac{{x}^{\mathrm{2}} \mathrm{cos}{x}}{\mathrm{sin}{x}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {x}\mathrm{cot}{xdx}\:\:\:\left({using}\:{IBP}\right) \\ $$$${I}=\mathrm{0}+\mathrm{2}\left[{x}\mathrm{ln}\left(\mathrm{sin}{x}\right)\right]_{\mathrm{0}} ^{\frac{.\pi}{\mathrm{2}}} −\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\right){dx} \\ $$$${I}=\mathrm{0}+\mathrm{0}−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\right){dx} \\ $$$${but}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\right){dx}=−\frac{\pi}{\mathrm{2}}\mathrm{ln2} \\ $$$$\because{I}=−\mathrm{2}\left[−\frac{\pi}{\mathrm{2}}\mathrm{ln2}\right]=\pi\mathrm{ln2} \\ $$$$\because\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{{x}}{\mathrm{sin}{x}}\right)^{\mathrm{2}} {dx}=\pi\mathrm{ln2} \\ $$$${by}\:{mathdave}\left(\mathrm{08}/\mathrm{09}/\mathrm{2020}\right) \\ $$
Commented by mnjuly1970 last updated on 09/Sep/20
$${bravo}\:{bravo}\:{bravo}\:{sir}\: \\ $$$${peace}\:{be}\:{upon}\:{you}\:…{mr}\: \\ $$$${dave} \\ $$
Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\:\mathrm{sir} \\ $$
Answered by maths mind last updated on 09/Sep/20
![let tg((x/2))=t⇒dx=((2dt)/(1+t^2 )) Ω=∫_0 ^1 ((4arctan^2 (t))/((((2t)/(1+t^2 )))^2 )).((2dt)/((1+t^2 )))=2∫_0 ^1 (1+t^2 )((arctan^2 (t)dt)/t^2 ) =2∫_0 ^1 ((arctan^2 (t))/t^2 )dt_(=2I) +2∫_0 ^1 arctan^2 (t)dt_(=2J) By Part J=[tarctan^2 (t)]_0 ^1 −∫((2t)/(1+t^2 ))arctan(t)dt=(π^2 /(16))−∫((2tarctan(t)dt)/(1+t^2 )) =(π^2 /(16))−[ln(1+t^2 )arctan(t)]_0 ^1 +∫_0 ^1 ((ln(1+t^2 ))/(1+t^2 ))dt =(π^2 /(16))−ln(2)(π/4)+∫_0 ^1 ((ln(1+t^2 ))/(1+t^2 ))dt t=tg(δ)⇒∫_0 ^1 ((ln(1+t^2 ))/(1+t^2 ))dt=∫_0 ^(π/4) ln(1+tg^2 (δ))dδ we use ∫_0 ^(π/2) ln(cos(x))dx=−((πln(2))/2)⇒ −2∫_0 ^(π/2) ln(cos(δ))dδ=−2.((−π)/2)ln(2)=πln(2) 2∫_0 ^(π/4) ln(tg(t))dt=−2G=−2∫_0 ^(π/4) ln(cos(δ))dδ+2∫_(π/4) ^(π/2) ln(cos(δ))dδ =−2∫_0 ^(π/4) ln(cos(δ))dδ−πln(2)−2∫_0 ^(π/4) ln(cos(δ))dδ⇒−2∫_0 ^(π/4) ln(cos(δ)dδ =−G+((πln(2))/2) ⇒J=(π^2 /(16))+((πln(2))/4)−G I by part=lim_(x→0) [−(1/t)arctan^2 (t)]_x ^1 +∫_0 ^1 ((2arctan(t))/(t(1+t^2 )))dt −(π^2 /(16))+2∫_0 ^1 ((1/t)−(t/(1+t^2 )))arctan(t)dt =−(π^2 /(16))+2∫_0 ^1 ((arctan(t))/t)dt_(=2G) −∫_0 ^1 ((2t)/(1+t^2 ))arcran(t){done lign(5)) =−(π^2 /(16))+2G+ln(2)(π/4)−G=−(π^2 /(16))+G+((πln(2))/4) 2I+2J=πln(2) G catalan canstant E∫_0 ^1 ((arctan(t))/t)dt=∫_0 ^1 (1/t)Σ_(k=0) ^∞ (((−1)^k t^(2k+1) )/(2k+1))dt=Σ_(k≥0) (((−1)^k )/((2k+1)^2 ))=G..true by partE=[ln(t)arctan(t)]_0 ^1 −∫_0 ^1 ((ln(t))/(1+t^2 ))dt =−∫_0 ^1 ((ln(t))/(1+t^2 ))dt (t=tg(δ))⇒=−∫_0 ^(π/4) ln(tg(δ))dδ proved what we used in lign/11](https://www.tinkutara.com/question/Q112644.png)
$${let}\:{tg}\left(\frac{{x}}{\mathrm{2}}\right)={t}\Rightarrow{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{4}{arctan}^{\mathrm{2}} \left({t}\right)}{\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} }.\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)\frac{{arctan}^{\mathrm{2}} \left({t}\right){dt}}{{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arctan}^{\mathrm{2}} \left({t}\right)}{{t}^{\mathrm{2}} }{dt}_{=\mathrm{2}{I}} +\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {arctan}^{\mathrm{2}} \left({t}\right){dt}_{=\mathrm{2}{J}} \\ $$$${By}\:{Part}\: \\ $$$${J}=\left[{tarctan}^{\mathrm{2}} \left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{arctan}\left({t}\right){dt}=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}−\int\frac{\mathrm{2}{tarctan}\left({t}\right){dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}−\left[{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){arctan}\left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}−{ln}\left(\mathrm{2}\right)\frac{\pi}{\mathrm{4}}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${t}={tg}\left(\delta\right)\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left(\mathrm{1}+{tg}^{\mathrm{2}} \left(\delta\right)\right){d}\delta \\ $$$${we}\:{use}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\left({x}\right)\right){dx}=−\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\Rightarrow \\ $$$$−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\left(\delta\right)\right){d}\delta=−\mathrm{2}.\frac{−\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)=\pi{ln}\left(\mathrm{2}\right) \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({tg}\left({t}\right)\right){dt}=−\mathrm{2}{G}=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\delta\right)\right){d}\delta+\mathrm{2}\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\left(\delta\right)\right){d}\delta \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\delta\right)\right){d}\delta−\pi{ln}\left(\mathrm{2}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\delta\right)\right){d}\delta\Rightarrow−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left(\delta\right){d}\delta\right. \\ $$$$=−{G}+\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$\Rightarrow{J}=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{4}}−{G} \\ $$$${I}\:{by}\:{part}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\left[−\frac{\mathrm{1}}{{t}}{arctan}^{\mathrm{2}} \left({t}\right)\right]_{{x}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{arctan}\left({t}\right)}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$$−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{{t}}−\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right){arctan}\left({t}\right){dt} \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arctan}\left({t}\right)}{{t}}{d}\underset{=\mathrm{2}{G}} {{t}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{arcran}\left({t}\right)\left\{{done}\:{lign}\left(\mathrm{5}\right)\right) \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\mathrm{2}{G}+{ln}\left(\mathrm{2}\right)\frac{\pi}{\mathrm{4}}−{G}=−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+{G}+\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{4}} \\ $$$$\mathrm{2}{I}+\mathrm{2}{J}=\pi{ln}\left(\mathrm{2}\right)\:\: \\ $$$${G}\:{catalan}\:{canstant}\: \\ $$$${E}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{arctan}\left({t}\right)}{{t}}{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{t}}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {t}^{\mathrm{2}{k}+\mathrm{1}} }{\mathrm{2}{k}+\mathrm{1}}{dt}=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }={G}..{true} \\ $$$${by}\:{partE}=\left[{ln}\left({t}\right){arctan}\left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:\left({t}={tg}\left(\delta\right)\right)\Rightarrow=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({tg}\left(\delta\right)\right){d}\delta\:{proved}\:{what}\: \\ $$$${we}\:{used}\:\:{in}\:\:{lign}/\mathrm{11} \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 09/Sep/20
$${thank}\:{you}\:{so}\:{much}\:. \\ $$
Answered by mnjuly1970 last updated on 09/Sep/20
![my solution. ∫_0 ^(π/2) log(sin(x))dx =−(π/2)log(2) l.h.s=^(i.b.p) [xlog(sin(x))]_0 ^(π/2) −∫_0 ^(π/2) xcot(x)dx =^(lim_(x→0^+ ) (xlog(sin(x)))=0) −∫_0 ^(π/2) xcot(x)dx =^(i.b.p.Again) −{[(x^2 /2)cot(x)]_0 ^(π/2) + (1/2)∫_0 ^(π/2) (x^2 /(sin^2 (x)))dx = =−(1/2)∫_0 ^(π/2) (x^2 /(sin^2 (x)))dx =r.h.s=−(π/2)log(2) ∴ ∫_0 ^(π/2) ((x/(sin(x))))^2 dx =πlog(2) ▲ m.n.july 1970#](https://www.tinkutara.com/question/Q112696.png)
$${my}\:{solution}. \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}\left({x}\right)\right){dx}\:=−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right)\: \\ $$$${l}.{h}.{s}\overset{{i}.{b}.{p}} {=}\left[{xlog}\left({sin}\left({x}\right)\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {xcot}\left({x}\right){dx}\: \\ $$$$\:\overset{{lim}_{{x}\rightarrow\mathrm{0}^{+} } \left({xlog}\left({sin}\left({x}\right)\right)\right)=\mathrm{0}} {=}\:\:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {xcot}\left({x}\right){dx} \\ $$$$\:\:\:\:\:\overset{{i}.{b}.{p}.{Again}} {=}\:−\left\{\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{cot}\left({x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}^{\mathrm{2}} }{{sin}^{\mathrm{2}} \left({x}\right)}{dx}\:=\:\right. \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}^{\mathrm{2}} }{{sin}^{\mathrm{2}} \left({x}\right)}{dx}\:={r}.{h}.{s}=−\frac{\pi}{\mathrm{2}}{log}\left(\mathrm{2}\right) \\ $$$$\therefore\:\:\:\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{{x}}{{sin}\left({x}\right)}\right)^{\mathrm{2}} {dx}\:=\pi{log}\left(\mathrm{2}\right)\:\blacktriangle \\ $$$${m}.{n}.{july}\:\mathrm{1970}# \\ $$$$ \\ $$$$ \\ $$
